Teste de Hipóteses

Introdução

É uma metodologia estatística que nos auxilia a tomar decisões sobre uma ou mais populações baseado na informação obtida da amostra.

Nos permite verificar se os dados amostrais trazem evidência que apoiem ou não uma hipótese estatística formulada.

Ao tentarmos tomar decisões, é conveniente a formulação de suposições ou de conjeturas sobre as populações de interesse, que, em geral, consistem em considerações sobre parâmetros (\(\mu, \sigma^2, p\)) das mesmas.

Essas suposições, que podem ser ou não verdadeiras, são denominadas de Hipóteses Estatísticas.

Em muitas situações práticas o interesse do pesquisador é verificar a veracidade sobre um ou mais parâmetros populacionais (\(\mu, \sigma^2, p\)) ou sobre a distribuição de uma variável aleatória.

Exemplos:

A produtividade média milho no estado (SC) é de 2500 kg/ha;
A proporção de peças defeituosas no unidade de fabricação é de 0,10;
A propaganda produz efeito positivo nas vendas;
Os métodos de ensino produzem resultados diferentes de aprendizagem

Um dos primeiros trabalhos sobre testes foi publicado em 1710 (John Arbuthnot);

Um dos primeiros procedimentos estatísticos que chega perto de um teste, no sentido moderno foi proposto por Karl Pearson em 1900. Esse foi o famoso teste do Qui-quadrado, utilizado para comparar uma distribuição de frequência observada com uma distribuição teoricamente assumida.

A ideia de testar hipóteses foi posteriormente codificada e elaborada por R. A Fischer (1925), que considerou os dados como um vetor de variáveis aleatórias que pertenciam a uma distribuição de probabilidade…

Uma outra abordagem (competitiva a de Fischer) foi estabelecida por J. Neyman e Egon Pearson (1928)…

Mais tarde, Lehmann (1993) argumentou que de fato era possível unificar as formulação, combinando as melhores características das duas abordagens…

Hipóteses Estatísticas

Teste de hipótese

O teste de hipóteses fornecem ferramentas que nos permitem rejeitar ou não rejeitar uma hipótese estatística através da evidencia fornecida pela amostra.

Vamos abordar o tópico com os seguintes exemplos:

Exemplo 1

Um engenheiro postula a hipótese que a fração de itens defeituosos em um certo processo é de \(p =0.10\).

O experimento é observar uma amostra aleatória do produto em questão, e suponha que \(n=100\) itens foram testados e \(12\) deles eram defeituosos, dessa forma foi estimada uma proporção de \(\hat{p}=0.12\) a partir da amostra.

É razoável que esta evidência não refuta a condição de que a proporção populacional é \(p=0.10\) ou seja não rejeitamos a hipótese postulada anteriormente.

No entanto, não rejeitaríamos também se fosse \(p=0.12\) ou talvez \(p=0.15\)…

Podemos expressar isso formalmente em termos de um teste de hipótese estatístico como:

\[ H_0: p = 10 \\ \space \\ H_1: p \ne 10 \] A afirmação de que \(H_0: p = 10\) é chamanda de hipótese nula, e a afirmação \(H_1: p \ne 10\) é chamada de hipótese alternativa.

A hipótese alternativa \(H_1\) ainda pode especificar, \(<\) ou \(>\) além da diferença \(\ne\).

Sempre estabeleceremos a hipótese nula \(H_0\) como uma afirmação de igualdade.

Exemplo 2

Poderiamos estar interessados em verificar se a taxa média de queima de um propelente é ou não \(\mu = 60\) cm/s.

Podemos expressar isso formalmente em termos de um teste de hipótese estatístico como:

\[ H_0: \mu = 60 \\ \space \\ H_1: \mu \ne 60 \] Mais uma vez a hipótese alternativa \(H_1\) ainda pode especificar, \(<\) ou \(>\) além da diferença \(\ne\).

Testes de hipóteses estatísticas

Uma vez formuladas as hipóteses gostaríamos de testa-las para que uma decisão seja tomada, seja em favor da hipótese nula ou da hipótese alternativa. Para tanto precisamos de algumas evidências, ou seja de informação.

Dessa forma a obtenção das evidências ou informação será a partir de uma amostra, e quanto maiores as evidências (entende-se por amostra) mais fácil será a tomadad de decisão.

Dado o exemplo anterior vamos construir o teste de hipótese.

Vamos verificar se a taxa média de queima de um propelente é ou não \(\mu = 60\) cm/s.

\[ H_0: \mu = 60 \\ \space \\ H_1: \mu \ne 60 \]

Para isso tomaremos uma amostra (tamanho \(n\)) onde será avaliada a taxa média de queima dessa amostra (\(\overline{x}\)). Lembre-se que a média amostral é uma estimativa da média populacional.

Caso a média amostral \(\overline{x}\) seja próxima da média populacional \(\mu = 60\) podemos supor que \(\mu = 60\) é a verdadeira média populacional (\(H_0\)), e caso seja um valor muito diferente desse, poderíamos supor que \(\mu \ne 60\) é válida, \(H_1\). Assim neste caso a média amostral é a estatística do teste.

Sabemos que a média amostral pode assumir muitos valores distintos, sendo assim podemos supor critérios para se rejeitar ou não rejeitar a hipótese nula, do tipo, se a média estiver entre \(58.5 \le \overline{x} \le 61.5\) não rejeitamos a \(H_0\), porém se a média for mais extrema que isso rejeitaremos. Chamaremos o região dos valores extremos de região crítica ou região de rejeição.

Tipos de Erros

Na tomada de decisão conforme estabelcido acima, dado algum critério, podemos obviamente estar comentendo algum erro. Chamaremos esses erros de erro do tipo I e II.

Erros do tipo I

Erro do Tipo I: Rejeitar a hipótese nula \(H_0\) quando ela é verdadeira

Erros do tipo II

Erro do Tipo II: Não Rejeitar a hipótese nula \(H_0\) quando ela é falsa

Decisão	Se \(H_0\) é verdadeira	Se \(H_0\) é falsa
Rejeitar \(H_0\)	Erro do Tipo I	Nenhum erro
Não Rejeitar \(H_0\)	Nenhum erro	Erro do Tipo II

Probabiliadde de cometer um erro na tomada de decisão

A probabilidade de cometer um erro (na tomada de decisão) pode ser explicitado da seguinte forma

Probabilidade do Erro do Tipo I

\[ \alpha = \mathbb{P}(erro \space do \space tipo \space I) = \mathbb{P}(rejeitar \space H_0|H_0 \space verdadeira) \] A probabilidade do erro do tipo I, \(\alpha\) é chamado de nível de significância, ou erro \(\alpha\), ou ainda tamanho do teste.

Probabilidade do Erro do Tipo II

\[ \beta = \mathbb{P}(erro \space do \space tipo \space II) = \mathbb{P}(não \space rejeitar \space H_0|H_0 \space falsa) \]

Potência ou Poder do Teste

\[ 1 - \beta = \mathbb{P}(rejeitar \space H_0|H_1 \space verdadeira) \] O poder do teste ou potência é a probabilidade de rejeitar a hipótese nula \(H_0\), quando a hipótese alternativa \(H_1\) é verdadeira

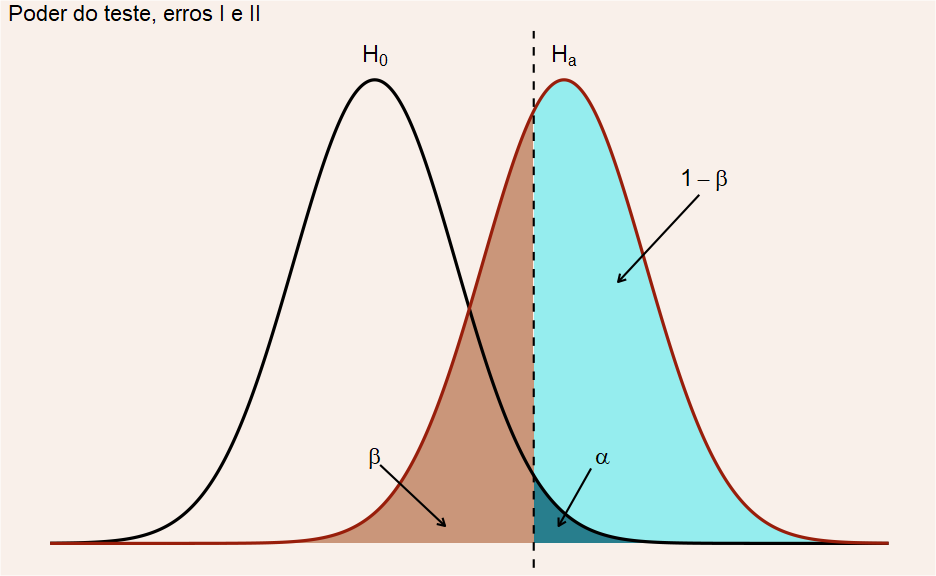
Poder do Teste

Pacote em R para auxiliar na visualização do teste de hipóteses

Um pacote em R (Plothtests) está sendo desenvolvido com o intuito de fornecer insights a respeito do teste de hipóteses, de a forma a facilitar o entendimento do significado das quantidades calculadas no teste, bem como a distribuição da estatística amostral, valores críticos para tomada de decisão e valor de probabilidade (Valor-P).

O procedimento para instalação do pacote se encontra abaixo:

install.packages("devtools")
library(devtools)
install_github("Zibetti/Plothtests")
library(Plothtests)

O teste de hipóteses e a construção da estatística de teste

Exemplo - Teste de hipóteses - 1 - diferença de médias, variâncias desconhecidas e iguais

Nos testes de hipóteses utilizamos os conhecimentos de estimação de parâmetros e probabilidade na tomada de decisão a favor de uma hipótese com base nas evidências (amostra) que lançamos mão.

Suponha a situação em que desejamos comparar dois treinamentos de atletas, o treinamento A e o treinamento B. Ambos tipos de treinamentos foram aplicados em atletas da mesma faixa etária e de similar performance, sendo como suposição, que qualquer melhora ou piora na performance dos atletas pode ser atribuída ao tipo de treinamento aplicado.

Para testar a hipótese de que o treinamento A faz com que a performance dos atletas seja inferior daqueles que realizaram o treinamento B testaremos as seguintes hipóteses:

\(H_o:\) de que não existe diferença na performance média dos atletas treinados com o A ou B.
\(H_1:\) de que a performance média dos atletas treinados com o A é inferior ao de B.

Cabe notar que a hipótese alternativa poderia ser de que a performance média dos atletas treinados com o A é superior ou ainda diferente…

Traduzindo isso em termos de parâmetros, temos:

\(H_o: \mu_A = \mu_B\)
\(H_1: \mu_A < \mu_B\)

Ou seja vamos testar a hipótese nula frente a hipótese alternativa. De certa forma verificaremos o quão inferior é o parâmetro do treinamento de A, e se é possível que essa diferença tenha vindo da hipótese alternativa.

O procedimento para se testar as hipóteses é coletar uma amostra de cada população treinada com cada uma das técnicas e verificar se as estimativas dos parâmetros são estatisticamente diferentes. Ou melhor, a diferença entre as estimativas é muito grande a ponto de não ser considerada ter vindo da hipótese nula, aquela que diz que ambos os treinamentos são iguais?

Quando dizemos que faremos o teste a partir de estimativas é por que não temos acesso à população, consequentemente desconhecemos os parâmetros populacionais. Caso conhecêssemos não precisaríamos realizar o teste, e sim somente verificar os parâmetros populacionais.

Somente como critério pedagógico vamos apresentar as populações subjacentes (porém assuma que não conhecemos nada a respeito dela).

performance_A = rnorm(100000,mean=12,sd=2.7)
performance_B = rnorm(100000,mean=13,sd=2.8)
hist(performance_A, freq=FALSE, breaks=100, col=rgb(0,0,1,1/4), xlim = c(0,20), ylim = c(0,0.3), main=expression(paste("População das performances de  A(",mu,'=12, ',~ sigma^{2},'=2.7) '," B(",mu,'=13, ',~ sigma^{2},'=2.8)')), xlab = "A     e     B")
hist(performance_B, freq=FALSE, breaks=100, col=rgb(1,0,0,1/4), xlim = c(0,20), add=TRUE)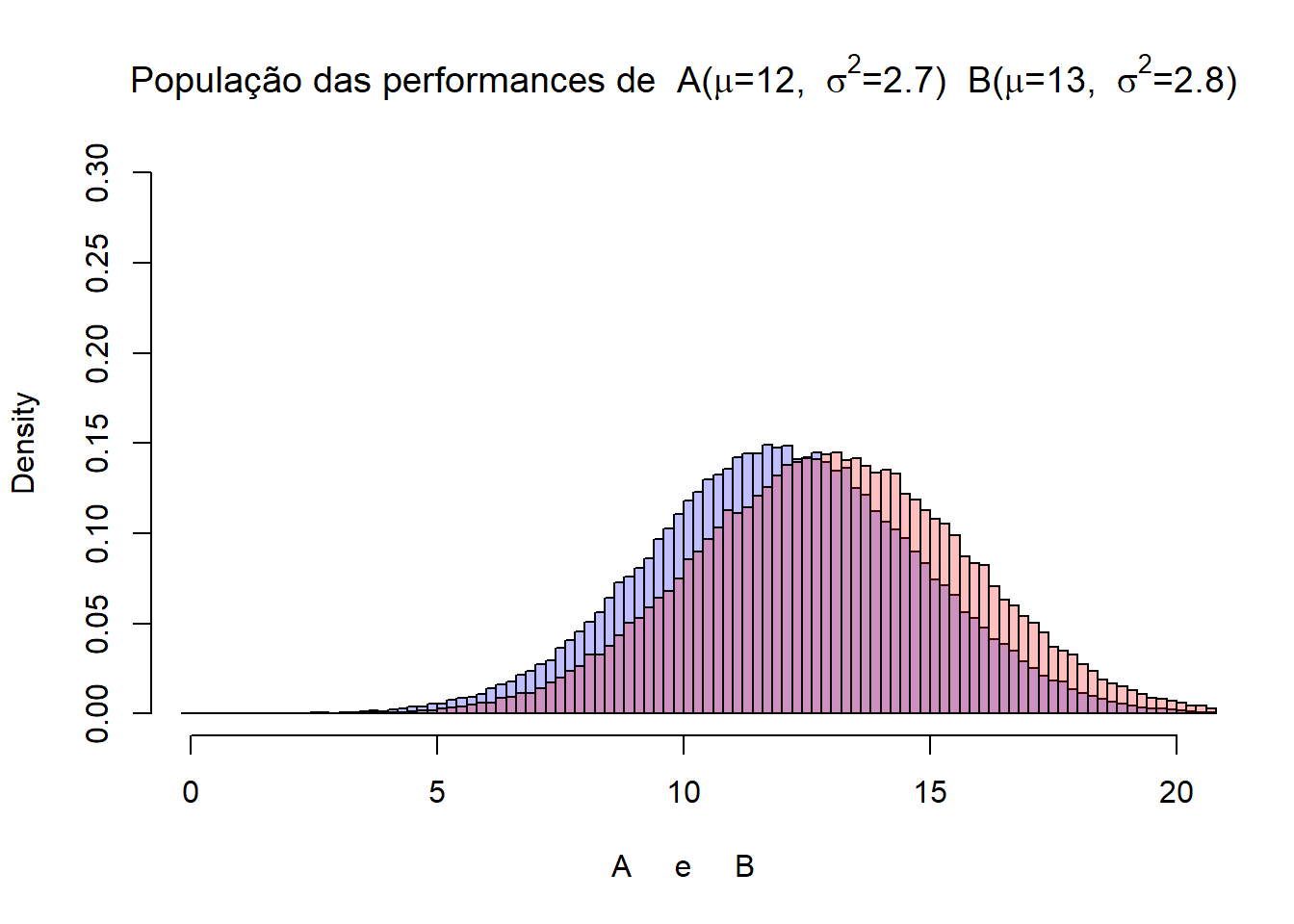

Agora tomaremos a nossa amostra de cada uma das populações, treinamento A e B, ambas com parâmetros desconhecidos (\(\mu_A\), \(\mu_B\), \(\sigma^2_A\) e \(\sigma^2_B\)). Para o presente caso tomaremos uma amostra aleatória de tamanho \(n = 15\) para cada treinamento. Uma vez com as amostras calcularemos as estatísticas amostrais (estimadores de parâmetros) e testaremos a hipótese nula para a diferença das médias.

n_A = 15
n_B = 15
amostra_A = rnorm(n_A,mean=12,sd=2.7)
amostra_B = rnorm(n_B,mean=13,sd=2.8)
#cat("média A = ", mean(amostra_A), "\ndes. padrão A = ", sd(amostra_A))
#cat("\nmédia B = ", mean(amostra_B), "\ndes. padrão B = ", sd(amostra_B))

\(\overline{x}_A =\) 11.8751483
\(\overline{x}_B =\) 13.2034837
\(S^2_A =\) 7.3349517
\(S^2_B =\) 8.3419714
\(S_A =\) 2.7083116
\(S_B =\) 2.8882471

Para este caso faremos um Teste-T (t-student), pois não conhecemos as variâncias populacionais (\(\sigma_A^2, \sigma_B^2\)), dessa forma calculamos uma estimativa da mesma (\(S_A^2,S_B^2\)), sendo essas variáveis aleatórias com uma distribuição aproximada pela \(\chi^2_{n-1}\). Considerando que \(\sigma_A^2 = \sigma_B^2 = \sigma^2\), utilizaremos ambas as informações para calcular uma estimativa única de \(\sigma^2\) que chamaremos de \(S_p^2\) (essa abordagem é explicada nos exemplos que seguem na próxima seção).

\[ T = \frac{(x_A - x_B) - (\mu_A - \mu_B)}{S_p \sqrt{\frac{1}{n_A} + \frac{1}{n_A}}} \]

# medias amostrais
x_A = mean(amostra_A)
x_B = mean(amostra_B)
# tamanos das amostras
n_A = 15
n_B = 15
# desvio padrão amostral
S_A = sd(amostra_A)
S_B = sd(amostra_B)
# variância amostral
S2_A = var(amostra_A)
S2_B = var(amostra_B)
# variancia combinada, onde o peso da amostra influência na combinação
S2_D = ((n_A - 1)/(n_A + n_B - 2))*S2_A + ((n_B - 1)/(n_A + n_B - 2))*S2_B
S_D = sqrt(S2_D)
# Calculando a diferença entre as duas amostras
t = (x_A - x_B)/(S_D*sqrt(1/n_A + 1/n_B))
t                      # estatística do teste

[1] -1.299341

T = t.test(amostra_A,amostra_B,alternative = "less")

Observe que a estatística diferença entre as médias \(\overline{x}_A - \overline{x}_B = -1.3283\) é tranformada na estatística \(t = -1.2993\) na distribuição \(H_0\). Dessa forma podemos calcular a probabilidade de um valor de diferença entre as médias ser igual a esse valor ou um valor mais extremo que esse (\(Valor-P\)).

Note que o \(Valor-P\) é 0.1022338, o que indica a probabilidade de cometermos o erro do tipo I a partir das evidências, ou seja a nossa amostra.

library(Plothtests)
plot_T_test(alpha = 0.05,
            alternative = "less",
            var.equal = "equal",
            m1 = x_A,
            m2 = x_B,
            v1 = S2_A,
            v2 = S2_B,
            n1 = 15,
            n2 = 15)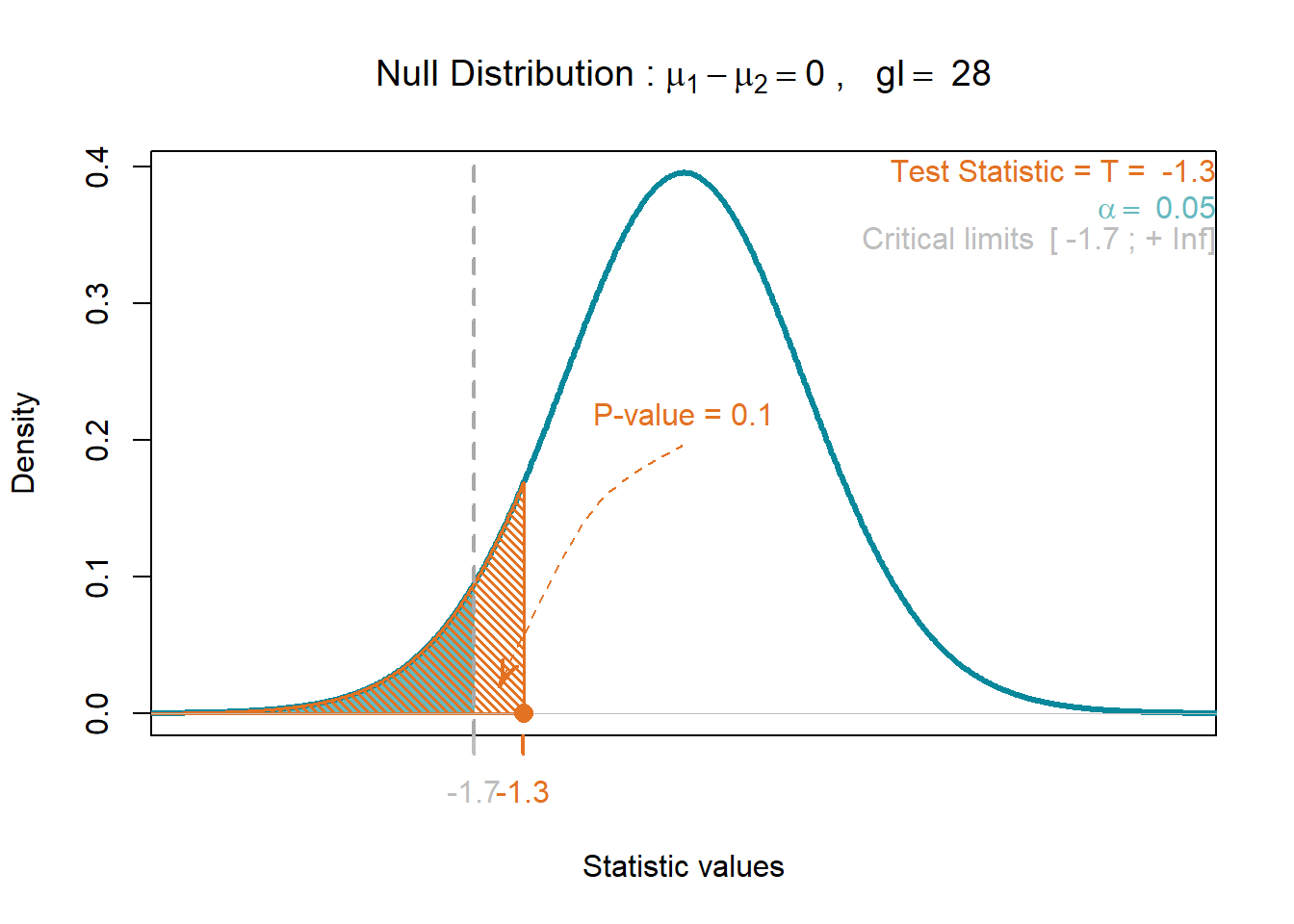

$test.statistic
[1] -1.299341

$df
[1] 28

$p.value
[1] 0.1022122

Para testar se de fato as variâncias são iguais ou não recorremos ao teste F, também como conhecido como razão de variâncias (pois nunca tomamos a diferença dessas quantidades).

Testando a hipótese da igualdade entre as variâncias

Primeiramente precisariamos estimar as variâncias, a partir desse ponto precisamos saber se as variâncias (estimadas) são iguais ou diferentes. O método para determinar o tamanho da relação de uma variância com a outra é dada pela razão de variâncias.

Dessa forma nosso primeiro passo será determinar se as variâncias são iguais ou não.

Vamos então realizar na verdade um teste de hipóteses para a variância.

A variância amostral (ou seja a variável aleatória variância amostral) possui uma distribuição de densidade de probabilidade, que é aproximadamente uma qui-quadrado \(\chi^2\), ou seja a variável aleatória variância amostral (\(S^2\)) possui uma distribuição qui-quadrado.

Na verdade o que podemos provar é que a quantidade \(\big(\frac{n-1}{\sigma^2}\big)S^2 \sim \chi^2_{n-1}\), e ainda assim desde que a variável aleatória em questão tenha distribuição normal.

Um vez que pretendemos testar a razão de duas variáveis aleatórias (variâncias amostrais) que se distribuiem dessa forma aproximada a (\(\chi^2_{n-1}\)), qual será a distribuição dessa nova variável aleatória?

Temos que essa razão de variâncias é nada mais é do que uma função de variáveis aleatórias.

Existe uma distribuição, desenvolvida por Ronald A. Fischer, distribuição F, que é uma função de duas variáveis aleatórias, ou seja a variável aleatória F é dada por:

\[ F = \frac{Q_1/gl_1}{Q_2/gl_2}\\ \\ Q_1 \sim \chi^2_{n_1-1}\\ \\ Q_2 \sim \chi^2_{n_2-1} \] Ou seja a distribuição F é a razão de duas variáveis aleatórias independentes com distribuição de qui-quadrado divido pelos seus resectivos graus de liberdade (\(gl\)). A distribuição possui dois parâmetros, que são os graus de liberdade do numerador e denominador, \(F_{gl_1,gl_2}\)

George W. Snedecor em seu livro Statisical Methods (1937) descreveu o teste de razão de variâncias, chamando de Teste-F em homenagem a Ronald A. Fischer.

Utilando as quantidades amostrais \(\big(\frac{n-1}{\sigma^2}\big)S^2\) que seguem uma distribuição de qui-quadrado com \(n-1\) graus de liberdade temos.

\[ F = \frac{\big(\frac{n_A-1}{\sigma_A^2}\big)S_A^2 / n_A-1}{\big(\frac{n_B-1}{\sigma_B^2}\big)S_B^2 / n_B-1}\\ \\ F = \frac{S_A^2}{S_B^2} \frac{\sigma_B^2}{\sigma_A^2} \sim F_{gl_A,gl_B}\\ \]

Sabemos, que \(F \sim F_{(gl_A,gl_B)}\) é uma distribuição F (Fischer) com graus de liberdade \(gl_A\) do numerador e \(gl_B\) do denominador, e essa distribuição é uma razão de duas variáveis aleatórias \(\chi^2_{n-1}\).

Abaixo segue uma simulação do resultado da razão de duas distribuições \(\chi^2_{n-1}\) e uma verificação da distribuição aproximada dessa variável aleatória, para fins didáticos. Ainda, o teste de Kolmogorov-Smirnov foi aplicado para verificar a adequação desses dados (\(F\)) à uma distribuição F. O resultado da estatística do teste foi \(D = 0.00061\), indicando que não pode ser rejeitado que esses dados vieram de uma distribuição F com os respectivos graus de liberdade.

S2_A = rchisq(1000000,df=8)# variância A - v.a. chi-quadrado, gl = 8
S2_B = rchisq(1000000,df=8)# variância A - v.a. chi-quadrado, gl = 8

par(mfrow=c(2,2))
hist(S2_A, freq=FALSE, breaks = 100, main=expression(S^2[A]))
hist(S2_B, freq=FALSE, breaks = 100, main=expression(S^2[B]))

F = (S2_A/8)/(S2_B/8)
hist(F, freq=FALSE, breaks = 100,xlim = c(0,70))

Fischer = rf(100000,df1 = 8, df=8)
hist(Fischer, freq=FALSE, breaks = 100, xlim = c(0,70))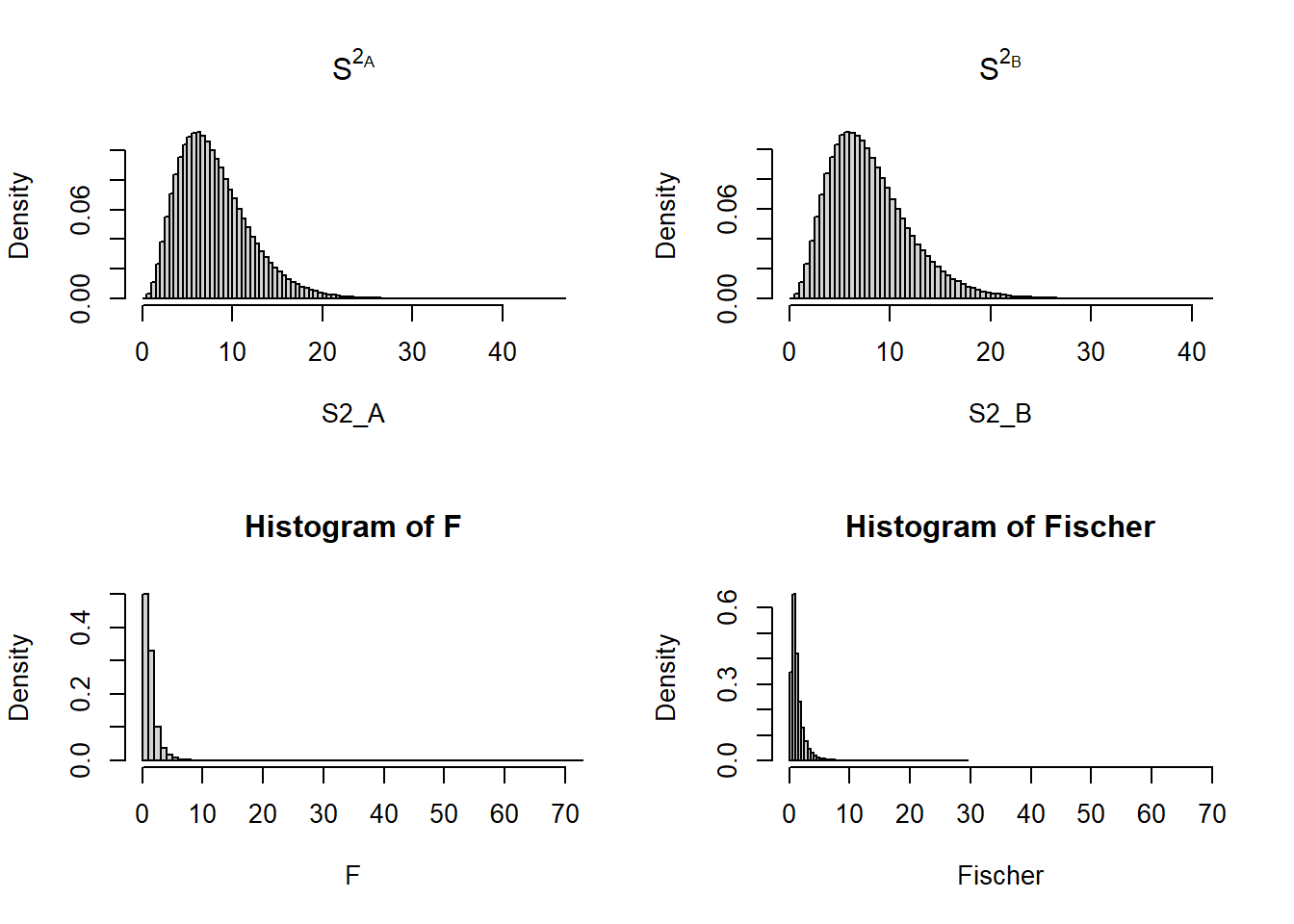

Note que a simulação não foi apresentada aqui, porém o codigo se encontra abaixo.

# code para verificar o ajuste dos dados da razao de chi-quadrados com a distribuição F
library(fitdistrplus)
fmle = fitdist(F, "f", start=list(8, 8)) # graus de liberdade df1=8 e df2=8
summary(fmle)
plot(fmle)
gofstat(fmle) # Goodness-of-fit

Para se verificar se as variâncias são iguais ou não é necessário recorrer ao teste F (inferência para duas variâncias de populações normais).

\[ H_0: \sigma_A^2 = \sigma_A^2 \\ H_1: \sigma_A^2 \ne \sigma_A^2 \\ \]

ou seja, a hipótese nula frente à uma hipótese alternativa, que pode ser, da diferença, ou seja a razão de variâncias ser diferente de 1, ou superior ou inferior à unidade,

\[ H_0: \sigma_A^2 = \sigma_A^2 \\ \]

sendo a hipótese alternativa uma das seguintes opções:

\[ H_1: \sigma_A^2 \ne \sigma_A^2 \\ \space \\ H_1: \sigma_A^2 > \sigma_A^2 \\ \space \\ H_1: \sigma_A^2 < \sigma_A^2 \\ \space \\ \] que são equivalentes às hipóteses:

\[ H_1: \frac{\sigma_A^2}{\sigma_A^2} \ne 1 \\ \space \\ H_1: \frac{\sigma_A^2}{\sigma_A^2} > 1 \\ \space \\ H_1: \frac{\sigma_A^2}{\sigma_A^2} < 1 \\ \space \\ \]

A estatística do teste é dada por:

Teste para diferença de variâncias

O teste de hipóteses para a diferença de variâncias de duas distribuições normais.

Hipótese nula: hipótese de nulidade, onde não há diferença entre as variâncias.

\(H_0: \frac{\sigma_A^2}{\sigma_B^2} = 1 \\\)

Estatística do teste: o quão a razão de variâncias se afastam da unidade \[ F = \frac{S_A^2}{S_B^2}\\ \]

Hipóteses alternativas disponíveis a testar:

\(H_1: \frac{\sigma_A^2}{\sigma_B^2} \ne 1\\\)
\(H_1: \frac{\sigma_A^2}{\sigma_B^2} > 1\\\)
\(H_1: \frac{\sigma_A^2}{\sigma_B^2} < 1\\\)

Voltando ao caso das amostras recolhidas A e B, testaremos a hipótese que as variâncias são diferentes entre si.

\(S^2_A =\) 7.3349517
\(S^2_B =\) 8.3419714

Hipóteses

Parâmetro de interesse a ser testado: Se \({\sigma_A^2}\ne {\sigma_B^2}\), consequentemente \(\frac{\sigma_A^2}{\sigma_B^2} = 1\)
Hipótese nula: \(H_0: \frac{\sigma_A^2}{\sigma_B^2} = 1\)
Hipótese alternativa: \(H_1: \frac{\sigma_A^2}{\sigma_B^2} \ne 1\)
Estatística do teste:

Note que por simplicidade no uso das probabilidades da F tabelada opta-se por obter o maior valor de F calculado, neste caso utilizando no numerador a maior variância amostral da comparação.

\[ F = \frac{S_A^2}{S_B^2}\\ \]

Decisão do teste: Rejeita-se \(H_0\) se o \(Valor-P\) (probabilidade de cometer o erro do Tipo I) for menor que \(\alpha\).

Erro do Tipo I: é a probabilidade em rejeitar a \(H_0\) sendo ela verdadeira.

Cálculos:

\[ F = \frac{S_A^2}{S_B^2} = \frac{8.3419}{7.3349} = 1.1372 \\ \]

library(Plothtests)
plot_F_test(alpha = 0.05,alternative = "two.sided", 
            df1 = 14,
            v1 = 8.3419,
            df2 = 14,
            v2 = 7.3349)

$test.statistic
[1] 1.137289

$df.num
[1] 14

$df.den
[1] 14

$p.value
[1] 0.8131681

Interpretação

Note que o \(Valor-P\) obtido foi de aproximadamente \(0.8131681\) (área hachurada), teste bilateral, devido a \(H_1\) ser postulada como a diferença. O \(Valor-P\) indica a probabilidade de comentermos o Erro do Tipo I com base na amostra, ou seja, rejeitarmos a \(H_0\) sendo ela verdadeira. Dessa forma a probabilidade de cometermos tal erro na tomada de decisão é demasiado elevado, superior ao valor arbitrário \(\alpha = 0.05\). Podemos dizer que não temos evidência nos dados que demonstrem diferença significativa entre as variâncias das amostras de preparações A e B.

Testando a hipótese da diferença de médias (\(\mu_A - \mu_B\)) de populações com variâncias desconhecidas

Voltando ao teste de médias …

Vamos considerar agora o teste de hipóteses para a diferença de duas médias populacionais, de populações normais com suas variâncias (\(\sigma^2_A,\sigma^2_B\)) desconhecidas. Para esses casos trocamos as variâncias populacionais por variâncias estimadas a partir das amostras (\(S^2_A, S^2_B\)).

Para tal situação poderiamos ter os seguintes casos: onde as variâncias são iguais, \(\sigma^2_A = \sigma^2_B\), e onde são diferentes \(\sigma^2_A \ne \sigma^2_B\).

Caso 1: Variâncias iguais \(\sigma^2_A = \sigma^2_B\)

Para se verificar se as variâncias são iguais ou não é necessário recorrer ao teste F (inferência para duas variâncias de populações normais).

Dessa forma suponha que tenhamos duas populações normais independentes com médias desconhecidas e variâncias desconhecidas porém iguais, e desejamos testar as seguintes hipóteses:

\[ H_0: \mu_A - \mu_B =\Delta_0 \\ H_1: \mu_A - \mu_B \ne \Delta_0 \\ \]

ou seja, a hipótese nula frente à uma hipótese alteranativa, que pode ser, da diferença entre as médias, ou da superioridade ou inferioridade de uma das médias,

\[ H_0: \mu_A - \mu_B = 0 \\ \]

sendo a hipótese alternativa uma das seguintes opções:

\[ H_1: \mu_A - \mu_B \ne 0\\ \space \\ H_1: \mu_A - \mu_B > 0\\ \space \\ H_1: \mu_A - \mu_B < 0\\ \space \\ \] Sabemos que a variância da diferença entre as variáveis aleatórias \(\overline{X}_A - \overline{X}_B\) é dada por:

\[ V(\overline{X}_A - \overline{X}_B) = \frac{\sigma^2}{n_A} + \frac{\sigma^2_B}{n_B}\\ \]

Sendo as variâncias iguais \(\sigma^2_A = \sigma^2_B = \sigma^2\), temos que:

\[ V(\overline{X}_A - \overline{X}_B) = \frac{\sigma^2}{n_A} + \frac{\sigma^2_B}{n_B} = \sigma^2(\frac{1}{n_A}+\frac{1}{n_B})\\ \]

Dessa forma combinar as duas estimativas (\(S^2_A, S^2_B\)) em uma única (\(S^2\)) parece razoável. O estimador combinado das duas variâncias estimadas é também chamado de pooled estimator,\(S^2_p\), e é dado por:

\[ S^2_p = \frac{n_A - 1}{n_A + n_B - 2}\cdot S^2_A + \frac{n_B - 1}{n_A + n_B - 2}\cdot S^2_B \]

Note que o estimador combinado nada mais é do que uma média das variâncias ponderada pelos tamanhos das amostras.

Assim a grandeza,

\[ t = \frac{\overline{X}_A -\overline{X}_B - (\mu_A - \mu_B)}{S_p \sqrt{\frac{1}{n_A} + \frac{1}{n_B}}} \] possui uma distribuição \(t\) com \(n_A + n_B - 2\) graus de liberadade.

A estatística do teste é dada por:

Teste para diferença de médias, variâncias desconhecidas e iguais

O teste de hipóteses para a diferença de médias de duas distribuições normais, variâncias desconhecidas e iguais.

Hipótese nula: hipótese de nulidade, onde não há diferença entre as médias, as médias seriam iguais.

\(H_0: \mu_A - \mu_B =\Delta_0 \\\)

Estatística do teste: o quão diferentes são as médias (diferença padronizada) \[ t_0 = \frac{\overline{X}_A -\overline{X}_B - \Delta_0}{S_p \sqrt{\frac{1}{n_A} + \frac{1}{n_B}}} \]

Hipóteses alternativas disponíveis a testar:

\(H_1: \mu_A - \mu_B \ne \Delta_0\\\)
\(H_1: \mu_A - \mu_B < \Delta_0\\\)
\(H_1: \mu_A - \mu_B > \Delta_0\\\)

Exemplo 1 - teste bilateral (\(\ne\))

Ensaios aplicados à amostra a duas preparações de concreto tem como objetivo verificar se existe diferença significativa na resistência entre os dois preparos. Para isso foram obtidas e testadas amostras de ambos os casos.

Tem se interesse em testar a hipótese de que existe diferença entre a resistência mecânica do preparo do \(A\) frente ao preparo \(B\). Foram retiradas 15 amostras do preparo \(A\) e 10 amostras do preparo \(B\). Os resultados obtidos a partir das amostras são apresentados na tabela abaixo.

Considere as variâncias iguais, e um \(\alpha = 0.05\).

Preparo	Média (\(\overline{x}\))	Desvio Padrão (\(s\))	Amostra (\(n\))
Preparo \(A\)	28 Mpa	4.1 MPa	15
Preparo \(B\)	26 Mpa	3.8 MPa	10

Hipóteses

Parâmetro de interesse a ser testado: Se \(\mu_A = \mu_B\), consequentemente \(\mu_A - \mu_B = 0\)
Hipótese nula: \(H_0: \mu_A - \mu_B = 0\)
Hipótese alternativa: \(H_1: \mu_A - \mu_B \ne 0\)
Estatística do teste:

\[ t_0 = \frac{\overline{X}_A -\overline{X}_B - 0}{S_p \sqrt{\frac{1}{n_A} + \frac{1}{n_B}}} \\ \space \\ \space \\ t_0 = \frac{\overline{X}_A -\overline{X}_B}{S_p \sqrt{\frac{1}{n_A} + \frac{1}{n_B}}} \\ \space \\ \space \\ t_0 = \frac{\overline{x}_A -\overline{x}_B}{s_p \sqrt{\frac{1}{n_A} + \frac{1}{n_B}}} \\ \]

Decisão do teste: Rejeita-se \(H_0\) se o \(Valor-P\) (probabilidade de cometer o erro do Tipo I) for menor que \(\alpha\).

Erro do Tipo I: é a probabilidade em rejeitar a \(H_0\) sendo ela verdadeira.

Cálculos:

\[ \begin{align} s^2_p &= \frac{15 - 1}{15 + 10 - 2}\cdot 4.1^2 + \frac{10 - 1}{15 + 10 - 2}\cdot 3.8^2 \\ \space \\ s^2_p &= (0.6087)\cdot 4.1^2 + (0.3913)\cdot 3.8^2 = 15.8826\\ \space \\ s_p &= 3.9853\\ \end{align} \]

n_A = 15
n_B = 10
s_A = 4.1
s_B = 3.8
s2_p = ((n_A - 1)/(n_A + n_B - 2))*s_A^2 + ((n_B - 1)/(n_A + n_B - 2))*s_B^2 
s_p  = sqrt(s2_p)
s_p

[1] 3.985299

\[ t_0 = \frac{\overline{x}_A -\overline{x}_B}{s_p \sqrt{\frac{1}{n_A} + \frac{1}{n_B}}} \\ \space \\ t_0 = \frac{28 -26}{3.9853 \sqrt{\frac{1}{15} + \frac{1}{10}}} \\ \space \\ t_0 = 1.23\\ \]

x_A = 28
x_B = 26
n_A = 15
n_B = 10
s_p = 3.9853
t0 = (x_A - x_B)/(s_p*sqrt(1/n_A + 1/n_B))
t0

[1] 1.229262

#
library(Plothtests)
plot_T_test(alpha = 0.05,
            alternative = "two.sided",
            var.equal = "equal",
            n1 = 15,
            m1 = 28,
            v1 = 4.1^2,
            n2 = 10, 
            m2 = 26,
            v2 = 3.8^2)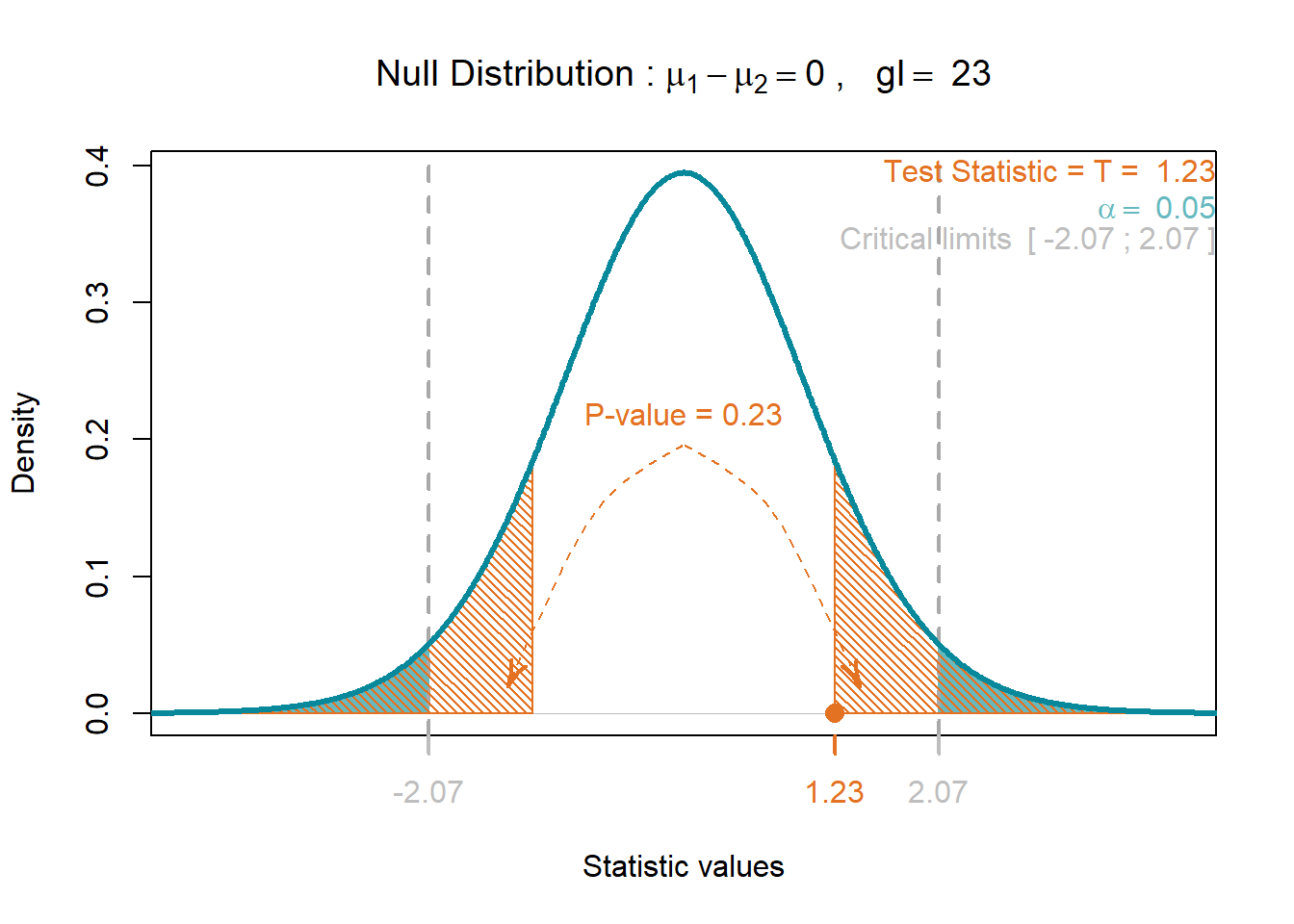

$test.statistic
[1] 1.229263

$df
[1] 23

$p.value
[1] 0.2314014

Interpretação

Note que o \(Valor-P\) obtido foi de aproximadamente \(Valor-P = 2*0.116 = 0.231\) (área hachurada), onde temos um teste bilateral, devido a \(H_1\) ser postulada como a diferença. O \(Valor-P\) indica a probabilidade de comentermos o Erro do Tipo I, ou seja, rejeitarmos a \(H_0\) sendo ela verdadeira. Dessa forma a probabilidade de cometermos tal erro na tomada de decisão é demasiado elevado, \(Valor-P\) = 0.231, superior ao valor de \(\alpha = 0.05\). Podemos dizer que não temos evidência nos dados que demonstrem diferença significativa entre as preparações A e B.

Exemplo 2 - teste unilateral (\(<\) ou \(>\))

Suponha agora que temos o interesse em verificar a hipótese de que a adição de um determinado aditivo em um dos preparados implica no aumento da sua resistência mecânica. Sendo assim o tratamento foi adicionar tal aditivio ao preparo \(A\) e testar frente ao preparo \(B\), sem aditivo. Para o referido teste foram retiradas 17 amostras do preparo \(A\) e 17 amostras do preparo \(B\). Os resultados obtidos a partir das amostras são apresentados na tabela abaixo.

Considere as variâncias iguais, e um \(\alpha = 0.05\).

As variâncias podem ser testadas para igualdade utilizando um Teste F (Fischer).

Preparo	Média (\(\overline{x}\))	Desvio Padrão (\(s\))	Amostra (\(n\))
Preparo com aditivo \(A\)	29 Mpa	3.7 MPa	17
Preparo sem aditivo \(B\)	26 Mpa	3.8 MPa	17

Hipóteses

Parâmetro de interesse a ser testado: Se \(\mu_A = \mu_B\), consequentemente \(\mu_A - \mu_B = 0\)
Hipótese nula: \(H_0: \mu_A - \mu_B = 0\)
Hipótese alternativa: \(H_1: \mu_A - \mu_B > 0\)
Estatística do teste:

\[ t_0 = \frac{\overline{x}_A -\overline{x}_B}{s_p \sqrt{\frac{1}{n_A} + \frac{1}{n_B}}} \\ \] - Decisão do teste: Rejeita-se \(H_0\) se o \(Valor-P\) (probabilidade de cometer o erro do Tipo I) for menor que \(\alpha\).

Erro do Tipo I: é a probabilidade em rejeitar a \(H_0\) sendo ela verdadeira.

Cálculos:

\[ \begin{align} s^2_p &= \frac{17 - 1}{17 + 17 - 2}\cdot 3.7^2 + \frac{17 - 1}{17 + 17 - 2}\cdot 3.8^2 \\ \space \\ s^2_p &= (0.5)\cdot 3.7^2 + (0.5)\cdot 3.8^2 = 14.065\\ \space \\ s_p &= 3.75\\ \end{align} \]

n_A = 17
n_B = 17
s_A = 3.7
s_B = 3.8
s2_p = ((n_A - 1)/(n_A + n_B - 2))*s_A^2 + ((n_B - 1)/(n_A + n_B - 2))*s_B^2
s_p  = sqrt(s2_p)
s_p

[1] 3.750333

\[ t_0 = \frac{\overline{x}_A -\overline{x}_B}{s_p \sqrt{\frac{1}{n_A} + \frac{1}{n_B}}} \\ \space \\ t_0 = \frac{29 -26}{3.75 \sqrt{\frac{1}{17} + \frac{1}{17}}} \\ \space \\ t_0 = 2.33\\ \]

x_A = 29
x_B = 26
n_A = 17
n_B = 17
s_p = 3.75
t0 = (x_A - x_B)/(s_p*sqrt(1/n_A + 1/n_B))
t0

[1] 2.332381

#
library(Plothtests)
plot_T_test(alpha = 0.05,
            alternative = "greater",
            var.equal = "equal",
            n1 = 17,
            m1 = 29,
            v1 = 3.7^2,
            n2 = 17, 
            m2 = 26,
            v2 = 3.8^2)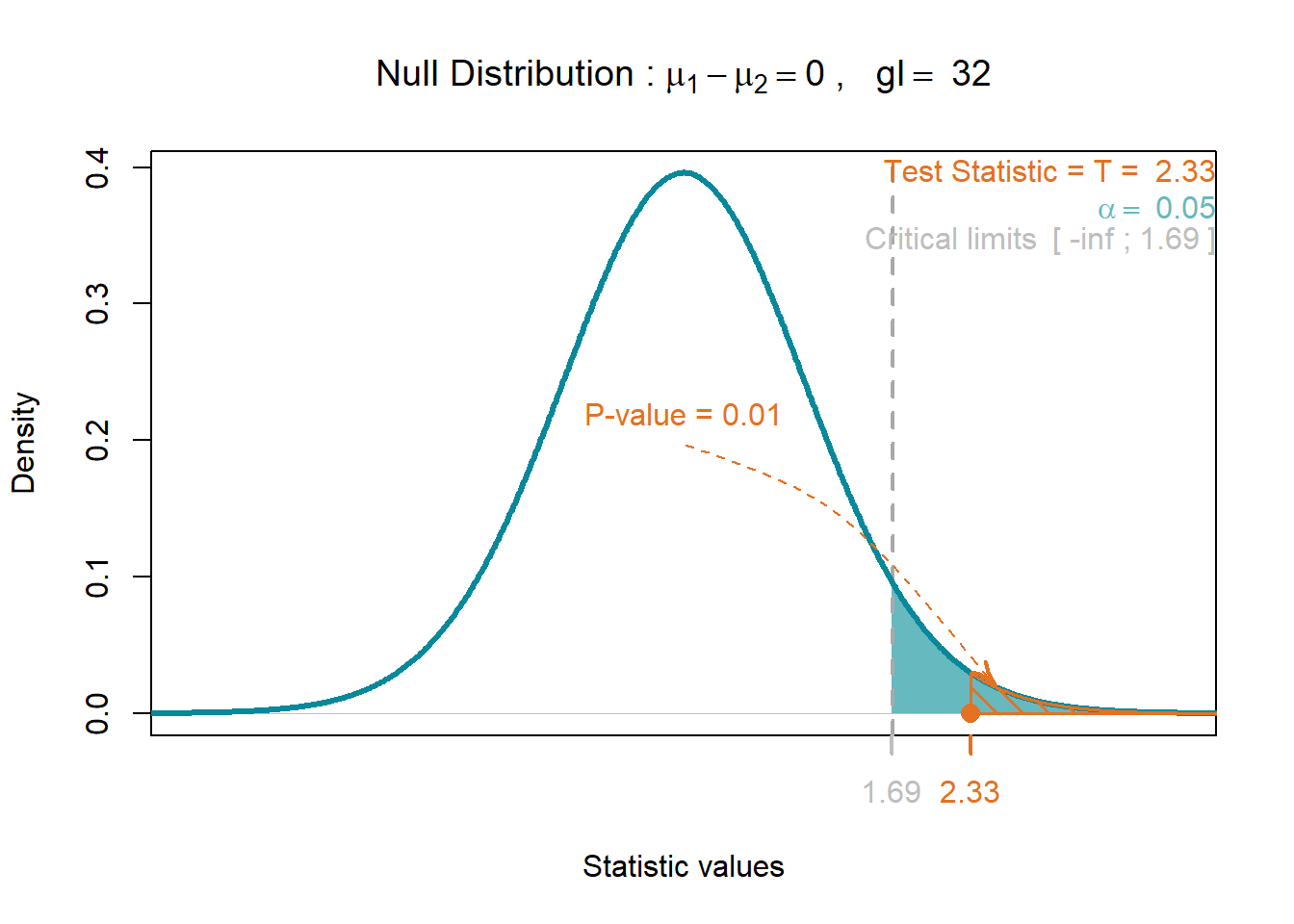

$test.statistic
[1] 2.332173

$df
[1] 32

$p.value
[1] 0.01307213

Interpretação

Note que o \(Valor-P\) obtido foi de aproximadamente \(Valor-P = 0.0131\), onde temos um teste unilateral, devido a \(H_1\) ser postulada como a a superioridade de uma das médias. O \(Valor-P\) indica a probabilidade de comentermos o Erro do Tipo I, ou seja, rejeitarmos a \(H_0\) sendo ela verdadeira. Dessa forma a probabilidade de cometermos tal erro na tomada de decisão é inferior ao valor de \(\alpha = 0.05\), \(Valor-P = 0.0131\). Podemos dizer que temos evidência nos dados que demonstrem um diferença estatísticamente significativa entre as preparações A e B. Em outras palavras o erro que estaria sendo cometido ao rejeitarmos \(H_0\) é algo em torno de 1.3 %.

Caso 2: Variâncias diferentes \(\sigma^2_A \ne \sigma^2_B\)

Para se verificar se as variâncias são iguais ou não é necessário recorrer ao teste F (inferência para duas variâncias de populações normais).

Dessa forma suponha que tenhamos duas populações normais independentes com médias desconhecidas e variâncias desconhecidas porém diferentes, e desejamos testar as hipóteses \(H_0\) versus uma \(H_1\).

Sabemos que a variância da diferença entre as variáveis aleatórias \(\overline{X}_A - \overline{X}_B\) é dada por:

\[ V(\overline{X}_A - \overline{X}_B) = \frac{\sigma^2}{n_A} + \frac{\sigma^2_B}{n_B}\\ \]

Assim a grandeza,

\[ t = \frac{\overline{X}_A -\overline{X}_B - (\mu_A - \mu_B)}{\sqrt{\frac{S^2_A}{n_A} + \frac{S^2_B}{n_B}}} \] possui uma distribuição \(t\) com \(v\) graus de liberadade. Para esse caso os graus de liberdade não serão mais \(n_A + n_B - 2\) e sim, calculados pela seguinte expressão:

\[ v = \frac{ \left( \frac{S^2_A}{n_A} + \frac{S^2_B}{n_B} \right)^2}{\frac{ \left( \frac{S^2_A}{n_A} \right)^2}{n_A - 1} + \frac{ \left( \frac{S^2_B}{n_B} \right)^2}{n_B - 1}} \]

A estatística do teste é dada por:

Teste para diferença de médias, variâncias desconhecidas e diferentes

O teste de hipóteses para a diferença de médias de duas distribuições normais, variâncias desconhecidas e diferentes.

Hipótese nula: hipótese de nulidade, onde não há diferença entre as médias, as médias seriam iguais.

\(H_0: \mu_A - \mu_B =\Delta_0 \\\)

Estatística do teste: o quão diferentes são as médias (diferença padronizada) \[ t_0 = \frac{\overline{X}_A -\overline{X}_B - \Delta_0}{\sqrt{\frac{S^2_A}{n_A} + \frac{S^2_B}{n_B}}} \]

Hipóteses alternativas disponíveis a testar:

\(H_1: \mu_A - \mu_B \ne \Delta_0\\\)
\(H_1: \mu_A - \mu_B < \Delta_0\\\)
\(H_1: \mu_A - \mu_B > \Delta_0\\\)

Exemplo 3 - teste bilateral (\(\ne\))

Um psicólogo estava interessado em explorar se os estudantes universitários do sexo masculino e feminino têm ou não diferentes comportamentos de condução. Havia uma série de maneiras que ela poderia quantificar comportamentos de condução. Ela optou por se concentrar na velocidade mais rápida já dirigida por um indivíduo. Portanto, a questão estatística em particular que ele formulou foi a seguinte:

Seria a maior velocidade média conduzida por estudantes universitários do sexo masculino diferente da maior velocidade média conduzida por estudantes universitários do sexo feminino?

Ele realizou um levantamento de uma amostra aleatória \(n_A = 34\) estudantes universitários do sexo masculino e \(n_B = 29\) estudantes universitários do sexo feminino.

Existe evidência suficiente no nível \(\alpha = 0.05\) para concluir que a maior velocidade média conduzida por estudantes universitários do sexo masculino difere da maior velocidade média de estudantes universitários do sexo feminino?

Considere as variâncias diferentes.

O resumo descritivo dos resultados de sua pesquisa:

Grupo	Média (\(\overline{x}\))	Desvio Padrão (\(s\))	Amostra (\(n\))
Masculino \(A\)	105.5	20.1	34
Feminino \(B\)	90.9	12.2	29

Hipóteses

Parâmetro de interesse a ser testado: Se \(\mu_A = \mu_B\), consequentemente \(\mu_A - \mu_B = 0\)
Hipótese nula: \(H_0: \mu_A - \mu_B = 0\)
Hipótese alternativa: \(H_1: \mu_A - \mu_B \ne 0\)
Estatística do teste:

\[ t_0 = \frac{\overline{x}_A -\overline{x}_B}{\sqrt{\frac{S^2_A}{n_A} + \frac{S^2_B}{n_B}}}\\ \]

Decisão do teste: Rejeita-se \(H_0\) se o \(Valor-P\) (probabilidade de cometer o erro do Tipo I) for menor que \(\alpha\).

Erro do Tipo I: é a probabilidade em rejeitar a \(H_0\) sendo ela verdadeira.

Cálculos:

Suposições: Vamos assumir que as variáveis aleatórias maiores velocidades (masculino e feminino) são normalmente distribuidas e que cada amostra é independente.

Calculando os graus de liberdade, \(v\):

\[ v = \frac{ \left( \frac{20.1^2}{34} + \frac{12.2^2}{29} \right)^2}{\frac{ \left( \frac{20.1}{34} \right)^2}{34 - 1} + \frac{ \left( \frac{12.2^2}{29} \right)^2}{29 - 1}} = 55.5 = 55 \]

Calculando a estatística do teste:

\[ t_0 = \frac{105.5 - 90.9}{\sqrt{\frac{20.1^2}{34} + \frac{12.2^2}{29}}} \\ \space \\ t_0 = 3.54\\ \]

x_A = 105.5
x_B = 90.9
n_A = 34
n_B = 29
t0 = (x_A - x_B)/(sqrt(20.1^2/n_A + 12.2^2/n_B))
t0

[1] 3.539453

#
library(Plothtests)
plot_T_test(alpha = 0.05,
            alternative = "two.sided",
            var.equal = "notequal",
            n1 = 34,
            m1 = 105.5,
            v1 = 20.1^2,
            n2 = 29, 
            m2 = 90.9,
            v2 = 12.2^2)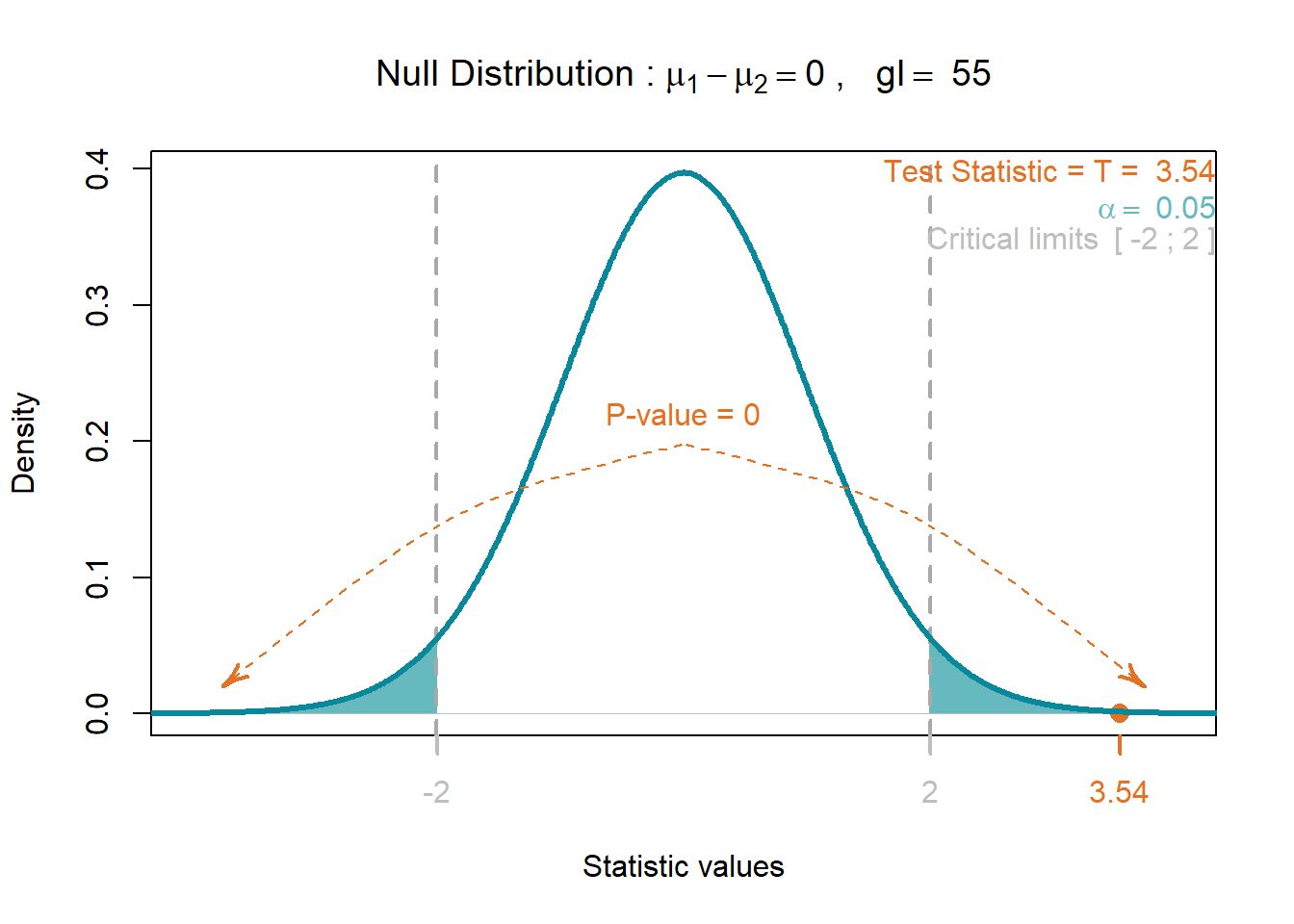

$test.statistic
[1] 3.539453

$df
[1] 55

$p.value
[1] 0.0008242127

Interpretação

O valor crítico para rejeição da hipótese nula \(H_0\) em favor da hipótese alternativa \(H_1\) é:

\[ t_0 > t_{0.025,55} = 2.004 \] Esse valor crítico pode ser obtido na tabela da distribuição t para \(\alpha/2 = 0.05/2 = 0.025\) pois é um teste bilateral, na curva com graus de liberadade igual a \(55\).

Note que o \(Valor-P\) obtido foi de aproximadamente \(p = 2*0.000412 = 0.000824\) (área hachurada), onde temos um teste bilateral, devido a \(H_1\) ser postulada como a diferença. O \(Valor-P\) indica a probabilidade de comentermos o Erro do Tipo I, ou seja, rejeitarmos a \(H_0\) sendo ela verdadeira. Dessa forma a probabilidade de cometermos tal erro na tomada de decisão é bastante pequeno, \(Valor-P\) = 0.000824, inferior ao valor de \(\alpha = 0.05\). Podemos dizer que temos evidência nos dados que demonstram diferença significativa entre as velocidades médias do grupo \(A\) e \(B\).

Este conteúdo está disponível por meio da Licença Creative Commons 4.0