Distribuição Normal

A distribuição normal é um modelo bastante útil na estatística, e não seria uma surpresa pois a soma de efeitos independentes (ou efeitos não muito correlacionados) deveriam, se houvesse muitos desses, se distribuir normalmente (sempre sujeito a certos pressupostos).

Nos séculos dezoito e dezenove, alguns matemáticos e físicos desenvolveram uma função densidade de probabilidade que descrevia os erros experimentais obtidos em medidas físicas Caire, 2012. De certa forma todo e qualquer processo de mensuração está sujeito a um erro de medida. Esse erro pode ter diferentes fontes, desde a variação de tempertura, tempo, entre inúmeras outras características não identificáveis.

Na época (século dezoito) a sua aplicação inicial era apenas como uma conveniente aproximação da distribuição binomial, mais tarde no século XIX a distribuição normal ganhou importância com os trabalhos de Abraham de Moivre (em The Doctrine of Chances), Pierre Simon Laplace e Carl Friedrich Gauss.

A grande utilidade dessa distribuição (função densidade de probabilidade) está associada ao fato de que aproxima de forma bastante satisfatória as curvas de frequências de medidas físicas, essa curva é conhecida como distribuição normal ou gaussina.

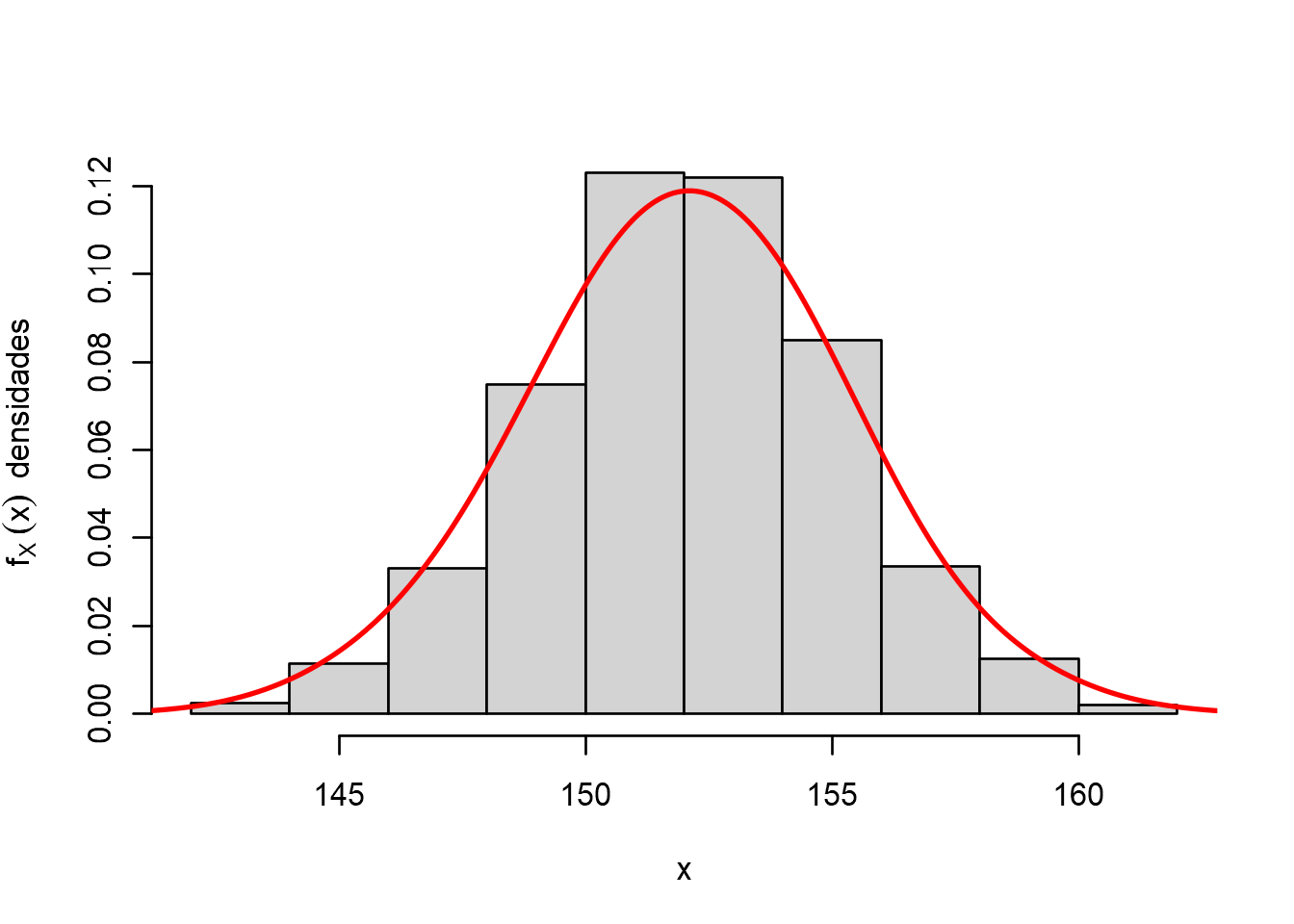
A distribuição normal possui dois parâmetros, a média \((\mu)\), ou seja onde está centralizada e a variância \((\sigma^2 > 0)\) que descreve o seu grau de dispersão. Ainda, é comum se referir a dispersão em termos de unidades padrão, ou seja desvio padrão \((\sigma)\). Cabe salientar que como qualquer outro modelo, dependendo dos parâmetros, teremos diferentes distribuições normais.

É importante lembrar que a variável \(X\) se distribui de forma contínua (variável contínua) de \(-\infty<x<+\infty\) e a área total sob a curva do modelo é unitária (ou seja 1).

Parâmetros

\(\mu\) é a média da distribuição
\(\sigma^2\) é a varância da distribuição
\(\sigma\) é o desvio padrão da distribuição, note que \(\sqrt{\sigma^2} = \sigma\)

Observe na figura abaixo uma distribuição normal com parâmetros \(\mu = 20,\sigma^2 = 4\) ou \((\sigma = 2)\).

x   = seq(10,30, by = 0.01)
media = 20       # média
var   = 4         # variância
dp    = sqrt(var) # desvio padrão 
# função de densidade
dx  = dnorm(x, mean = media, sd = sqrt(var))
#plot da função de densidade
plot(x,dx,type = "l", col = "red", ylab = bquote(f[X]~(x)~~"densidades"), xlab = "x", main =  bquote("N"~(mu==.(media)~","~sigma^2 == .(var))))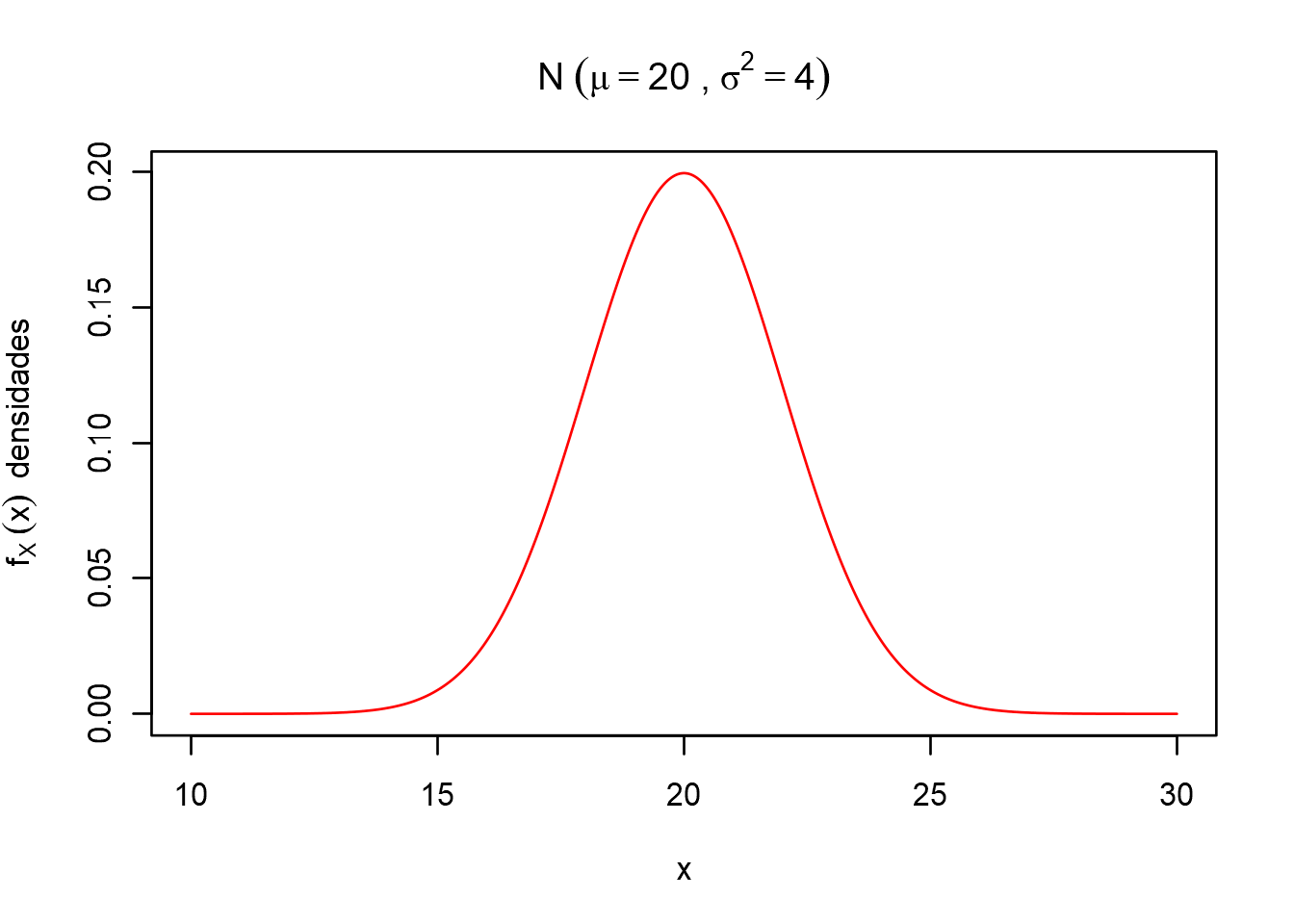

Exemplo de uma normal com parâmetros \(\mu = -15,\sigma^2 = 6\) ou \((\sigma = 2.44949)\).

x   = seq(-40,10, by = 0.01)
media = -15       # média
var   = 6         # variância
dp    = sqrt(var) # desvio padrão 
# função de densidade
dx  = dnorm(x, mean = media, sd = sqrt(var))
#plot da função de densidade
plot(x,dx,type = "l", col = "blue", ylab = bquote(f[X]~(x)~~"densidades"), xlab = "x", main =  bquote("N"~(mu==.(media)~","~sigma^2 == .(var))))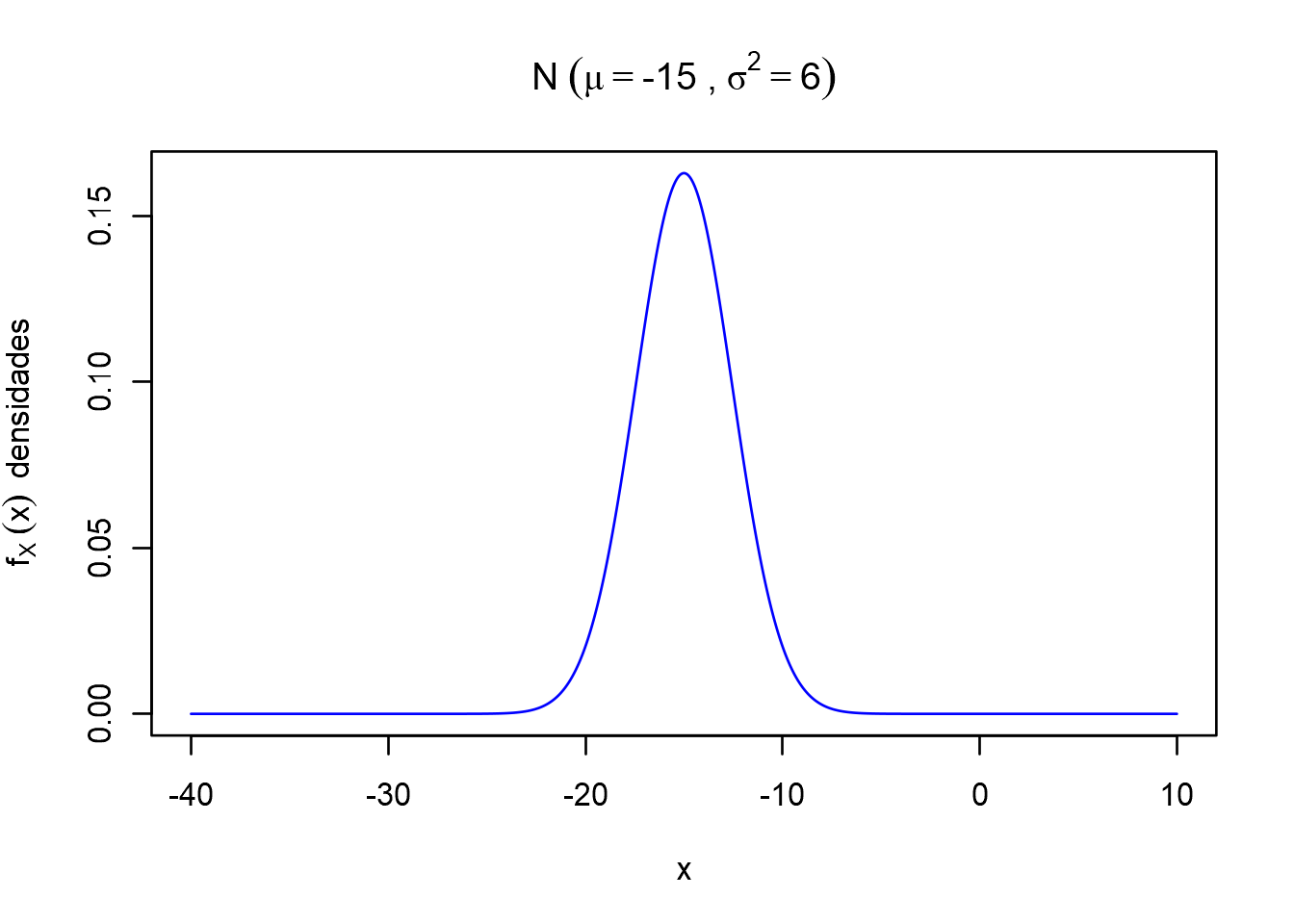

O modelo da função normal pode se expresso matemáticamente da seguinte forma:

Variável Aleatória Generalizada

Seja \(X\) uma variável aleatória contínua com média \(\mu\) em que \(-\infty < x < \infty\), e \(\sigma > 0\).

Função Densidade de Probabilidade

\[ f_X(x) = \frac{1}{{\sqrt {2\pi \sigma^2} }}e^{ - \frac{1}{2}\big(\frac{{x - \mu}}{\sigma}\big)^2} \quad -\infty< x < \infty \]

Podemos dizer que \(X\) possui uma distribuição normal e escrever \(X \sim N(\mu,\sigma^2)\).

Valor Esperado e variância

\[ E[X] = \mu \\ V(X) = \sigma^2 \]

Cálculo da Probabilidade

\[ \mathbb{P}(a < X < b) = \int\limits_a^b {{\frac{1}{{\sqrt {2\pi \sigma^2} }}e^{ - \frac{1}{2}\big(\frac{{x - \mu}}{\sigma}\big)^2}}}dx \]

Cabe notar que a integral da função densidade de probabilidade normal não possui solução analítica, sendo neste caso o seu cálculo deve ser realizado por uma aproximação, método numérico.

Por exemplo, pode-se utilizar o método numérico (regra de Newton-cotes, ponto-médio, trapezoidal, Simpson, etc..) ou outros métodos de aproximação.

Seja a área sob a curva no intervalo \([a,b]\) a probabilidade de algo ocorrer entre os valores de \(a\) até \(b\). É importante salientar que o valor da densidade, ou seja os valores de \(f_X(x)\) representam as densidades, enquanto que a área sob essas densidades é a probabilidade.

Caclulando as probabilidades de uma distribuição normal

Para uma distribuição normal dada por \(X \sim N(\mu=10,\sigma^2=4)\) ou \((\sigma = 2)\), podemos calcular as seguintes probabilidades, ou seja, as áreas sob a curva da distribuição normal utilizando o R (é só clicar em code). Logo mais, veremos como calcular utilizando a tabela da normal padrão.

Exemplo: a probabilidade entre os valores de \(X\) no intervalo \([8, 12]\)

#utilizando o graphics (pacote nativo)
x   = seq(0,20, by =0.01)
media = 10
var   = 4
# função de densidade
dx  = dnorm(x, mean = media, sd = sqrt(var))
#plot da função de densidade
plot(x,dx,type = "l", col = "blue", ylab = bquote(f[X]~(x)~~"densidades"), xlab = "x", main =  bquote("N"~(mu==.(media)~","~sigma^2 == .(var))))
# poligono para representar a área sob a curva
a = 8 # Limite inferior
b = 12 # Limite superior
da = dnorm(a,mean = media, sd = sqrt(var))   # Densidade no Limite inferior crítico
db = dnorm(b,mean = media, sd = sqrt(var))   # Densidade no Limite superior crítico

polygon(x = c(a, a  , x[a<x & x<b], b), # X = conjunto dos valores de a até b
        y = c(0, da , dx[a<x & x<b], 0),          # Y = conjunto das Density de a até b
        col = "red",
        density = c(20),
        angle = c(-45))

# cálculo da probabilidade de uma variável aleatória normal utilizando a função do R "pnorm"
# pnorm é a função cumulativa de probabilidade de uma distribuição normal
prob = pnorm(b,mean = media, sd = sqrt(var)) - pnorm(a,mean = media, sd = sqrt(var)) 

# legendas para o gráfico
legenda <- list( bquote( "Probabilidade =" ~ .(round(prob,4)) )  )
mtext(side = 3, do.call(expression, legenda), line=-2:-2, adj=1, col=c("red"))

# adicionado valores no eixo x
Map(axis, side=1, at = round(c(a,b),2),
    col.axis = c("red" , "red"),
    col.ticks = c("red", "red"),
    lwd=0, las=1,
    lwd.ticks = 2)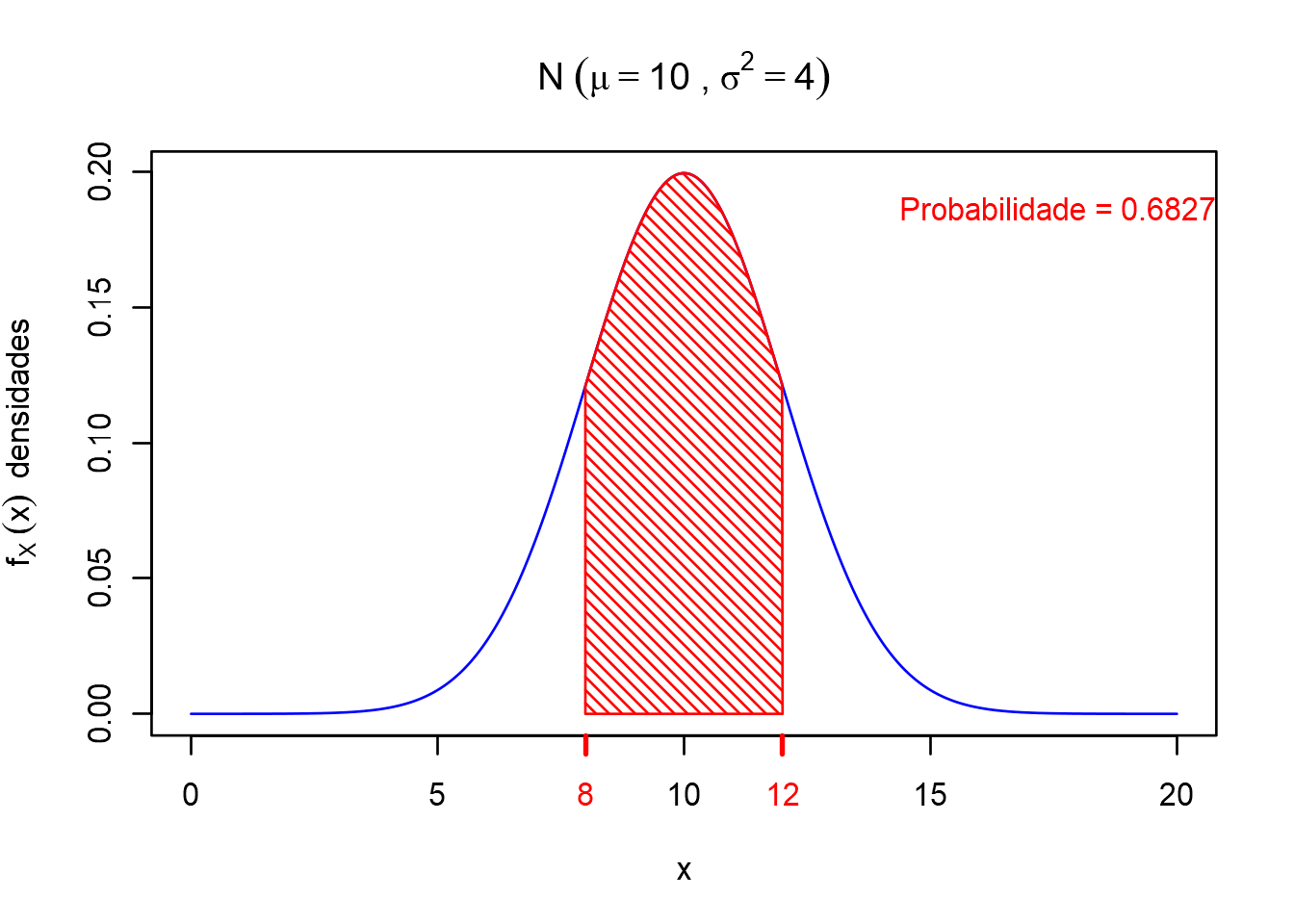

Exemplo: a probabilidade entre os valores de \(X\) no intervalo \([6, 14]\)

#utilizando o graphics (pacote nativo)
x   = seq(0,20, by =0.01)
media = 10
var   = 4
# função de densidade
dx  = dnorm(x, mean = media, sd = sqrt(var))
#plot da função de densidade
plot(x,dx,type = "l", col = "blue", ylab = bquote(f[X]~(x)~~"densidades"), xlab = "x", main =  bquote("N"~(mu==.(media)~","~sigma^2 == .(var))))
# poligono para representar a área sob a curva
a = 6 # Limite inferior
b = 14 # Limite superior
da = dnorm(a,mean = media, sd = sqrt(var))   # Densidade no Limite inferior crítico
db = dnorm(b,mean = media, sd = sqrt(var))   # Densidade no Limite superior crítico

polygon(x = c(a, a  , x[a<x & x<b], b), # X = conjunto dos valores de a até b
        y = c(0, da , dx[a<x & x<b], 0),          # Y = conjunto das Density de a até b
        col = "red",
        density = c(20),
        angle = c(-45))

# cálculo da probabilidade de uma variável aleatória normal utilizando a função do R "pnorm()"
# pnorm() é a função cumulativa de probabilidade de uma distribuição normal
prob = pnorm(b,mean = media, sd = sqrt(var)) - pnorm(a,mean = media, sd = sqrt(var))

# legendas para o gráfico
legenda <- list( bquote( "Probabilidade =" ~ .(round(prob,4)) )  )
mtext(side = 3, do.call(expression, legenda), line=-2:-2, adj=1, col=c("red"))

# adicionado valores no eixo x
Map(axis, side=1, at = round(c(a,b),2),
    col.axis = c("red" , "red"),
    col.ticks = c("red", "red"),
    lwd=0, las=1,
    lwd.ticks = 2)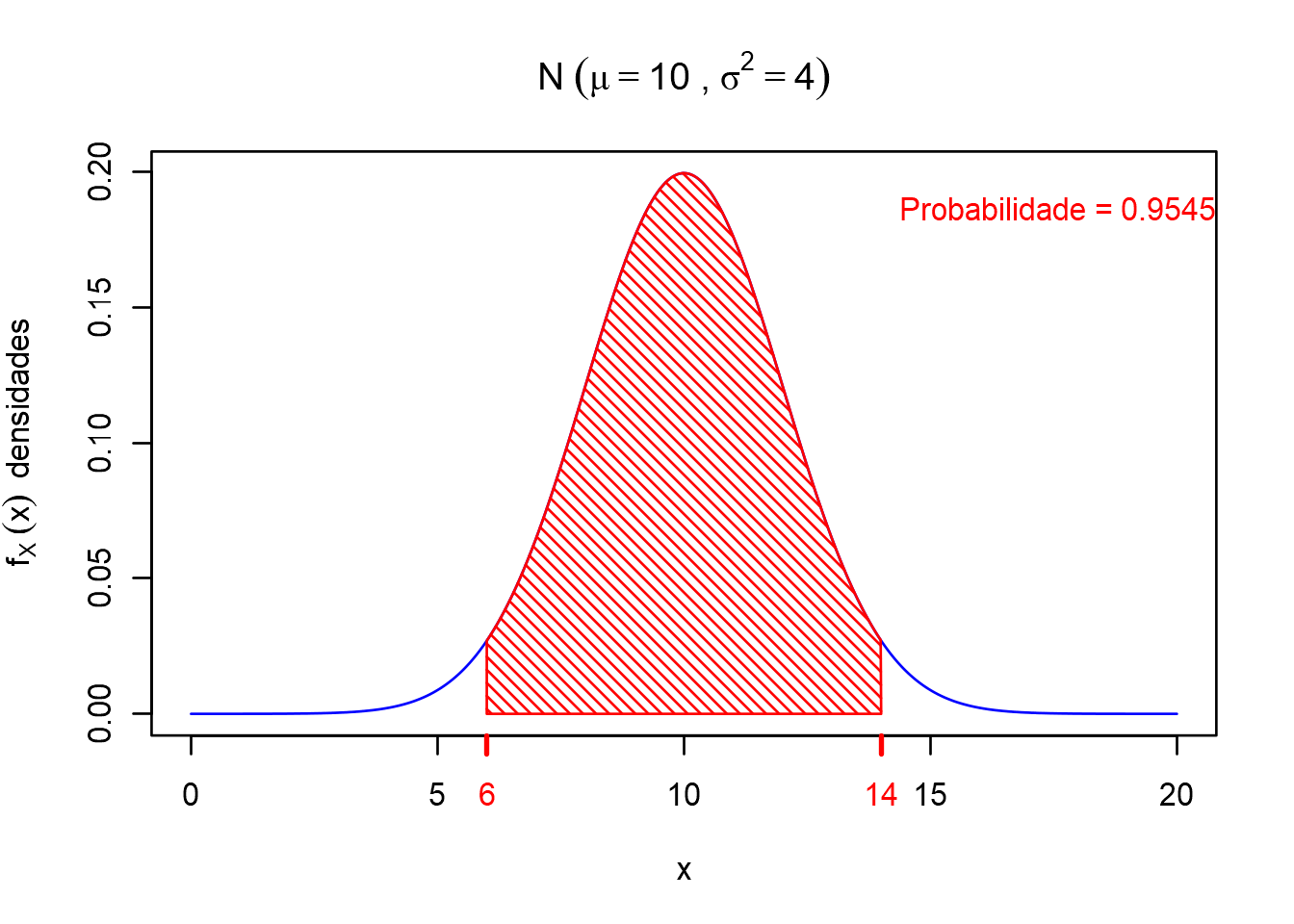

Exemplo: a probabilidade entre os valores de \(X\) no intervalo \([4, 16]\)

#utilizando o graphics (pacote nativo)
x   = seq(0,20, by =0.01)
media = 10
var   = 4
# função de densidade
dx  = dnorm(x, mean = media, sd = sqrt(var))
#plot da função de densidade
plot(x,dx,type = "l", col = "blue", ylab = bquote(f[X]~(x)~~"densidades"), xlab = "x", main =  bquote("N"~(mu==.(media)~","~sigma^2 == .(var))))
# poligono para representar a área sob a curva
a = 4 # Limite inferior
b = 16 # Limite superior
da = dnorm(a,mean = media, sd = sqrt(var))   # Densidade no Limite inferior crítico
db = dnorm(b,mean = media, sd = sqrt(var))   # Densidade no Limite superior crítico

polygon(x = c(a, a  , x[a<x & x<b], b), # X = conjunto dos valores de a até b
        y = c(0, da , dx[a<x & x<b], 0),          # Y = conjunto das Density de a até b
        col = "red",
        density = c(20),
        angle = c(-45))

# cálculo da probabilidade de uma variável aleatória normal utilizando a função do R "pnorm()"
# pnorm() é a função cumulativa de probabilidade de uma distribuição normal
prob = pnorm(b,mean = media, sd = sqrt(var)) - pnorm(a,mean = media, sd = sqrt(var))

# legendas para o gráfico
legenda <- list( bquote( "Probabilidade =" ~ .(round(prob,4)) )  )
mtext(side = 3, do.call(expression, legenda), line=-2:-2, adj=1, col=c("red"))

# adicionado valores no eixo x
Map(axis, side=1, at = round(c(a,b),2),
    col.axis = c("red" , "red"),
    col.ticks = c("red", "red"),
    lwd=0, las=1,
    lwd.ticks = 2)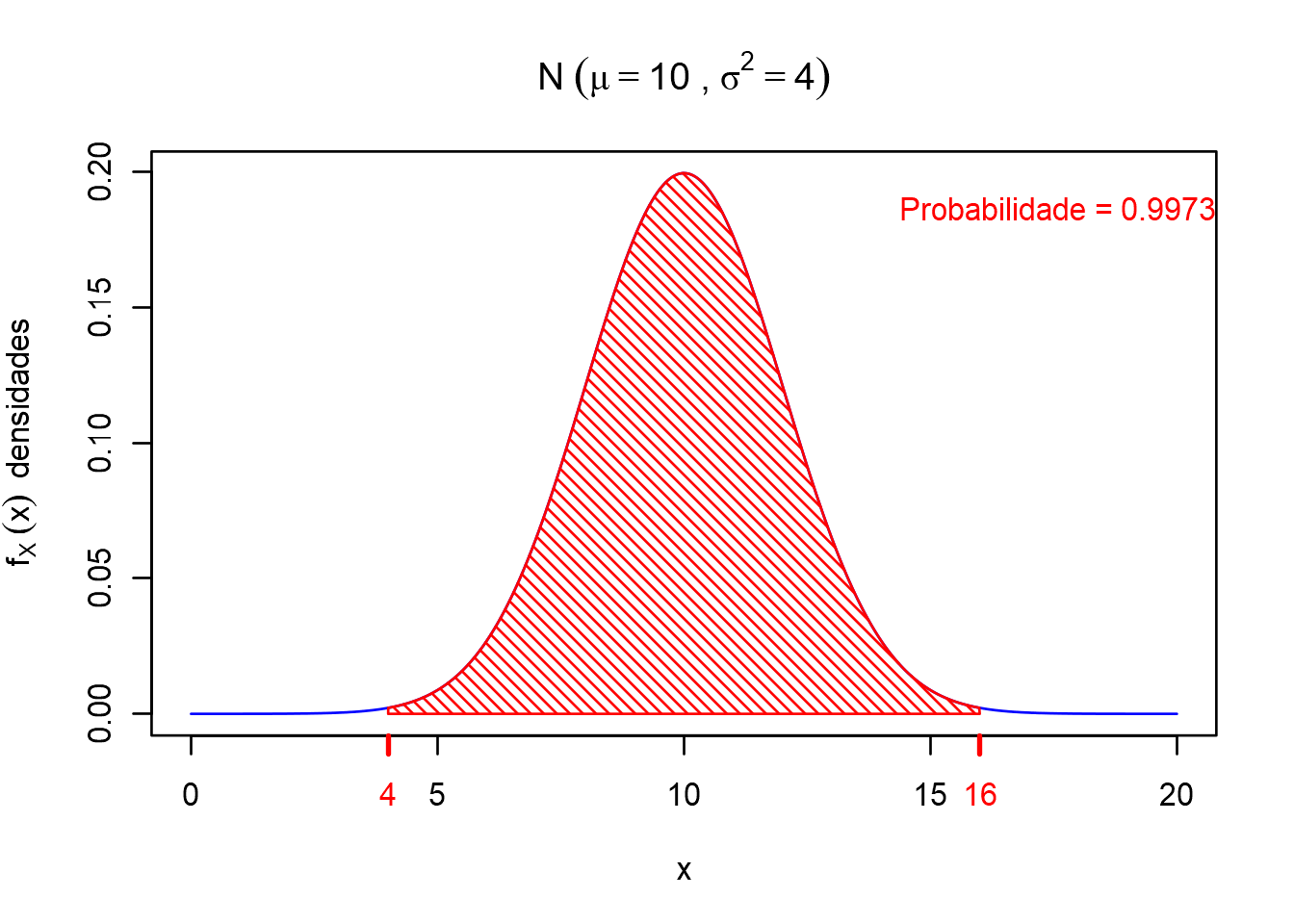

Resumindo, na distribuição normal acima onde \(X \sim N(\mu=10,\sigma^2=4)\) ou \((\sigma = 2)\), as probabilidades obtidas (numéricamente, utilizando o R) foram:

\[ \mathbb{P}(8 < X < 12) \approx 0.68 \] \[ \mathbb{P}(6 < X < 14) \approx 0.95 \] \[ \mathbb{P}(4 < X < 16) \approx 0.99 \]

Ou seja,

\[ \mathbb{P}(\mu - \sigma < X < \mu + \sigma) \approx 0.68 \] \[ \mathbb{P}(\mu - 2\sigma < X < \mu + 2\sigma) \approx 0.95 \] \[ \mathbb{P}(\mu - 3\sigma < X < \mu + 3\sigma) \approx 0.99 \]

Note que para uma distribuição normal isso é válido, sejam quais forem os parâmetros \((\mu, \sigma^2)\). Observe na figura abaixo a mesma situação com diferentes distribuições normais.

funcao_plot = function(media,var,a,b){
  #utilizando o graphics (pacote nativo)
  li  = media - 4.5*sqrt(var)
  ls  = media + 4.5*sqrt(var)
  x   = seq(li,ls, by =0.01) # limites de x e plot
  # função de densidade
  dx  = dnorm(x, mean = media, sd = sqrt(var))
  #plot da função de densidade
  plot(x,dx,type = "l", col = "blue", ylab = bquote(f[X]~(x)~~"densidades"), xlab = "x", main =  bquote("N"~(mu==.(media)~","~sigma^2 == .(var))))
  # poligono para representar a área sob a curva
  da = dnorm(a,mean = media, sd = sqrt(var))   # Densidade no Limite inferior crítico
  db = dnorm(b,mean = media, sd = sqrt(var))   # Densidade no Limite superior crítico
  
  polygon(x = c(a, a  , x[a<x & x<b], b), # X = conjunto dos valores de a até b
          y = c(0, da , dx[a<x & x<b], 0),          # Y = conjunto das Density de a até b
          col = "red",
          density = c(20),
          angle = c(-45))
  
  # Legendas
  prob = pnorm(b,mean = media, sd = sqrt(var)) - pnorm(a,mean = media, sd = sqrt(var)) 
  legenda <- list( bquote(~ .(round(prob,4)) )  )
  mtext(side = 3, do.call(expression, legenda), line=-2:-2, adj=1, col=c("red"))
  
  # adicionado valores no eixo x
  Map(axis, side=1, at = round(c(a,b),2),
      col.axis = c("red" , "red"),
      col.ticks = c("red", "red"),
      lwd=0, las=1,
      lwd.ticks = 2)
}

# plots
par(mfrow=c(2,3))
funcao_plot(30,4,30-1*sqrt(4),30+1*sqrt(4)) # plot 1,1
funcao_plot(30,4,30-2*sqrt(4),30+2*sqrt(4)) # plot 1,2
funcao_plot(30,4,30-3*sqrt(4),30+3*sqrt(4)) # plot 1,3
funcao_plot(100,15,100-1*sqrt(15),100+1*sqrt(15)) # plot 1,1
funcao_plot(100,15,100-2*sqrt(15),100+2*sqrt(15)) # plot 1,2
funcao_plot(100,15,100-3*sqrt(15),100+3*sqrt(15)) # plot 1,3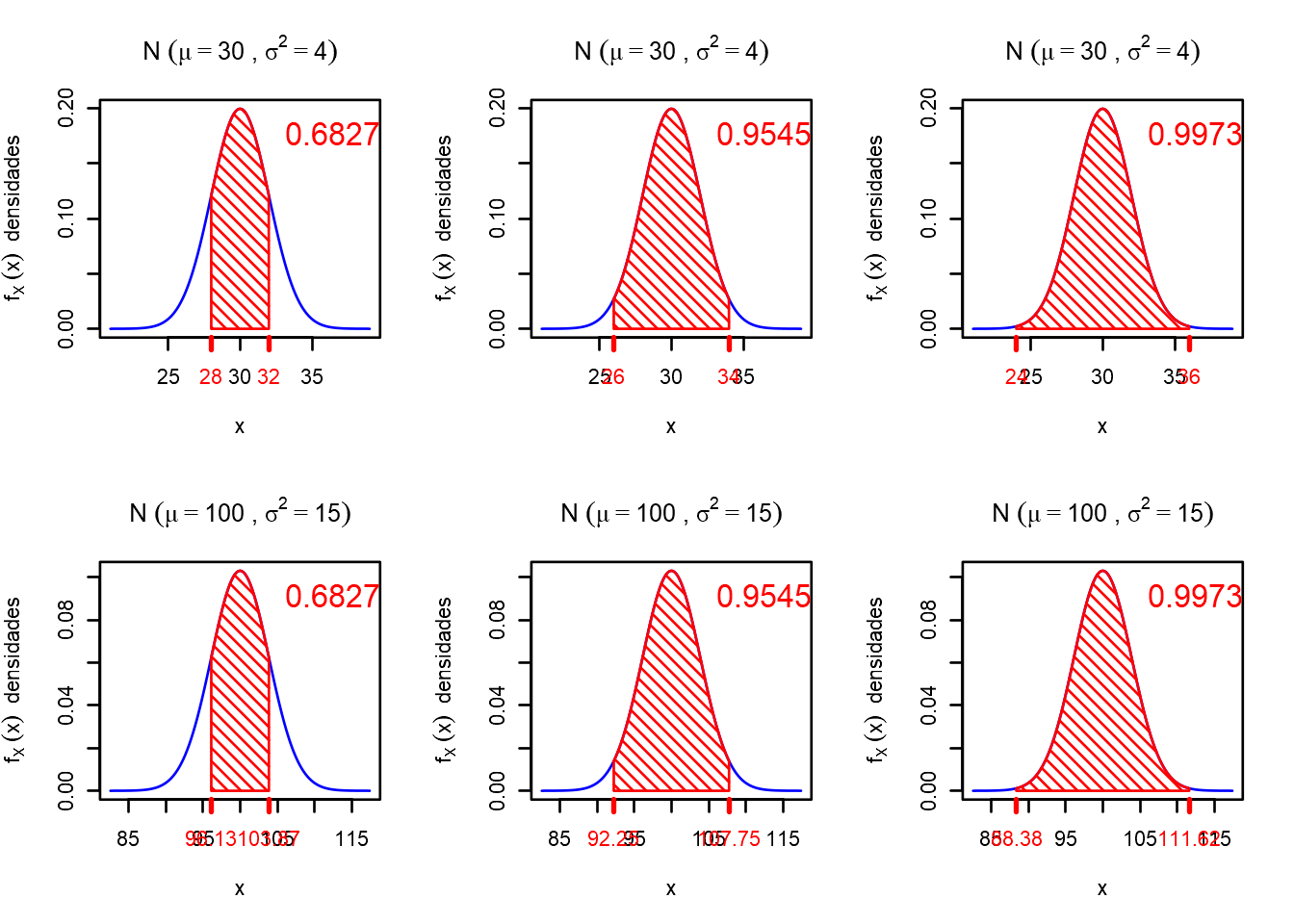

funcao_plot(0,1,0-1*sqrt(1),0+1*sqrt(1)) # plot 1,1
funcao_plot(0,1,0-2*sqrt(1),0+2*sqrt(1)) # plot 1,2
funcao_plot(0,1,0-3*sqrt(1),0+3*sqrt(1)) # plot 1,3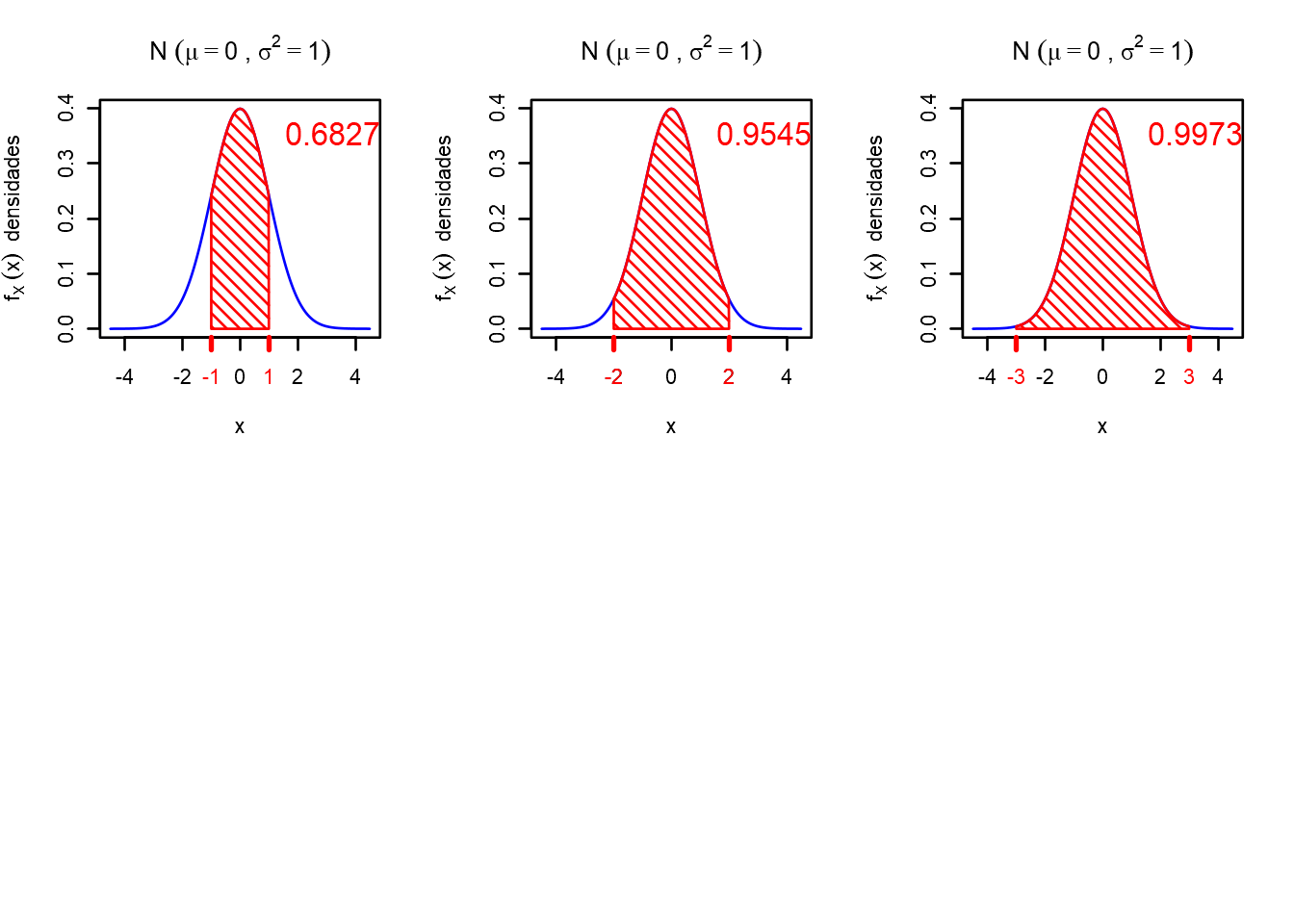

Agora a pergunta é, como podemos calcular a probabilidade de uma distribuição normal sem o auxílio do computador? Podemos utilizar a normal padronizada e uma tabela de probabilidades.

Distribuição Normal Padronizada

O que é a distribuição normal padronizada afinal?

É nada mais que uma distribuição normal sempre com os mesmos parâmetros, que são \(\mu=0,\sigma^2=1\).

Uma vez que essa distribuição possui sempre esses mesmos parâmetros significa dizer que sempre que desejar calcular uma probabilidade pode-se recorrer a uma tabela, onde valores de probabilidade já foram previamente calculados para essa única distribuição.

Note que o método para transformar uma normal qualquer \(X \sim N(\mu,\sigma^2)\) em uma normal padrão \(N(\mu=0,\sigma^2=1)\) é muito simples. Bastaria pensar da seguinte forma: como posso transformar uma normal com \(\mu=10\) em \(0\), bastaria pegar todos os valores de \(X\) e reduzir \(10\), ou seja \(X - \mu\), e para o desvio padrão (\(\sigma\)) se tornar \(1\), poderíamos, seja qual for o valor de \(\sigma\) dividir por ele mesmo.

Assim, qualquer distribuição normal pode ser padronizada, de forma que no processo de padronização dos valores da variável aleatória \((X)\) os parâmetros se tornem \(\mu = 0\) e \(\sigma^2 = 1\). Essa abordagem é dada pela definição de uma nova variável aleatória \(Z\), chamada de variável aleatória normal padronizada, dada pela função linear \(Z\).

\[ Z = \frac{X-\mu}{\sigma} \] onde \(X\) é uma variável aleatória normal com média \((\mu, \sigma^2>0)\).

Padronizando uma variável aleatória Normal

Se \(X\) for uma variável aleatória normal com \(E[X] = \mu\) e \(V(X) = \sigma^2\), a variável aleatória \(Z\) \[ Z = \frac{X-\mu}{\sigma} \] será uma variável aleatória normal, com \(E[Z]=0\) e \(V(Z)=1\). Ou seja, \(Z\) é uma variável aleatória normal padrão.

Como exemplo vamos transformar uma variável aleatória normal em uma normal padronizada, para isso todos os valores de \(X\) irão ser transformados linearmente em \(Z\).

Exemplo: para alguns valores da \(X \sim N(\mu=100,\sigma^2=25)\), vamos manualmente converter \(X = 85,90,95,100,105,110,115\) em valores \(Z\).

\[ \begin{aligned} X \quad &\rightarrow \quad Z = \frac{X -\mu}{\sigma}\\ \\ X=85 \quad &\rightarrow \quad Z = \frac{85 -100}{5} = -3\\ \\ X=90 \quad &\rightarrow \quad Z = \frac{90 -100}{5} = -2\\ \\ X=95 \quad &\rightarrow \quad Z = \frac{95 -100}{5} = -1\\ \\ X=100 \quad &\rightarrow \quad Z = \frac{100 -100}{5} = 0\\ \\ X=105 \quad &\rightarrow \quad Z = \frac{105 -100}{5} = 1\\ \\ X=110 \quad &\rightarrow \quad Z = \frac{110 -100}{5} = 2\\ \\ X=115 \quad &\rightarrow \quad Z = \frac{115 -100}{5} = 3\\ \end{aligned} \]

Os valores de \(Z\) também podem ser interpretados como o número de desvios padrão afastados da média, em uma distribuição normal padrão.

par(mfrow=c(1,2))
media = 100       # média
var   = 25         # variância
li    = media - 4.5*sqrt(var)
ls    = media + 4.5*sqrt(var)
x     = seq(li,ls, by =0.01) # limites de x e plot
# função de densidade
dx  = dnorm(x, mean = media, sd = sqrt(var))
#plot da função de densidade
plot(x,dx,type = "l", col = "blue", ylab = bquote(f[X]~(x)~~"densidades"), xlab = "x", main =  bquote("X~ N"~(mu==.(media)~","~sigma^2 == .(var))))

# transformando em Z
z = (x-media)/sqrt(var)
dz  = dnorm(z, mean = 0, sd = 1)
plot(z,dz,type = "l", col = "gray", ylab = bquote(f[Z]~(z)~~"densidades"), xlab = "z", main =  bquote("Z~ N"~(mu==0~","~sigma^2 == 1)))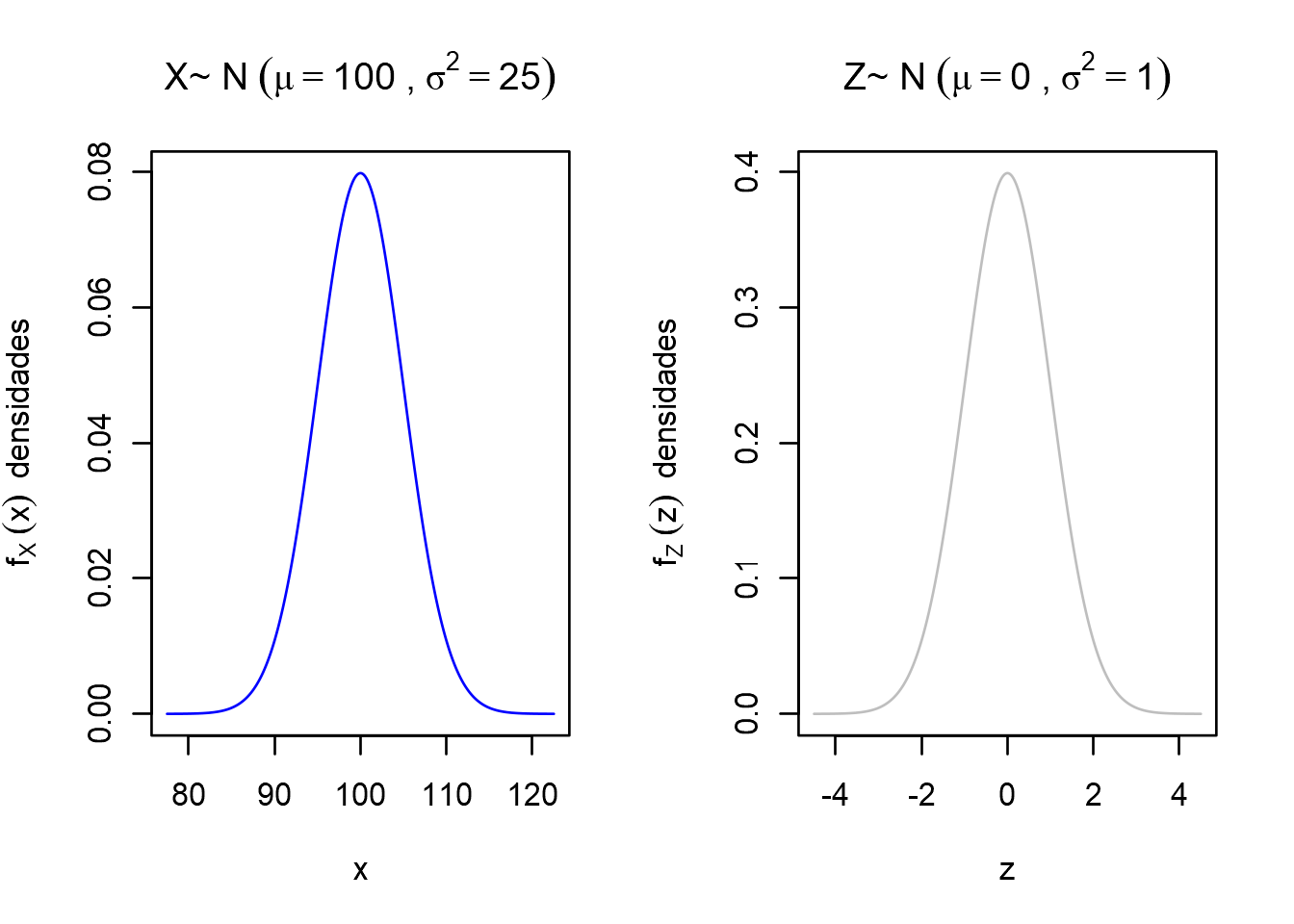

Dessa forma, é possível uma única vez obter a área sob a curva da normal padrão. Assim uma vez que a v.a. \(X\) é padronizada em \(Z\) é possível obter a área entre dois pontos sob a curva diretamente com o uso de uma tabela, e essa área representa uma probabilidade.

Exemplo - Normal 1

Os dados de uma pesquisa mostram algumas informações sobre o tempo de cirurgias para recostrução ACL em hospitais com alto volume de cirurgia. A partir dos dados foram calculados, o tempo médio de 129 minutos com um desvio padrão de 14 minutos.

Qual é a probabilidade de uma cirurgia ACL, em um hospital com alto volume de cirurgias, requerer um tempo maior do que dois desvios-padrão acima da média?
Qual é a probabilidade de uma cirurgia ACL, em um hospital com alto volume de cirurgias ser completada em menos de 100 minutos?
Em qual tempo a probabilidade de uma cirurgia ACL em um hospital com alto volume de cirurgias é igual a 0.95?
Se uma cirurgia requer 199 minutos, o que você conclui sobre o volume de tais cirurgias em um hospital? Explique.

Solução

Qual é a probabilidade de uma cirurgia ACL, em um hospital com alto volume de cirurgias, requerer um tempo maior do que dois desvios-padrão acima da média?

\[ 1 - \mathbb{P}(Z < 2) = 1 - \phi(2) = 0.0228 \]

1 - pnorm(2)

[1] 0.02275013

Qual é a probabilidade de uma cirurgia ACL, em um hospital com alto volume de cirurgias ser completada em menos de 100 minutos?

Seja \(X\) o tempo, onde \(X \sim N(129,14^2)\)

\[ Z = \frac{X-\mu}{\sigma} = \frac{100-129}{14} = -2.0714 \]

\[ \mathbb{P}(X < 100) =\phi(-2.0714) = 0.01916072 \]

pnorm(-2.0714)

[1] 0.01916072

Em qual tempo a probabilidade de uma cirurgia ACL em um hospital com alto volume de cirurgias é igual a 0.95?

z = qnorm(0.95) # fornece o valor de z para a probabilidade de 0.95
z

[1] 1.644854

x = z*14 + 129
x

[1] 152.028

O tempo em que 95 % das cirurgias irão acabaram é dentro de 152.028 minutos.

Se uma cirurgia requer 199 minutos, o que você conclui sobre o volume de tais cirurgias em um hospital? Explique.

De acordo com a distribuição sabemos que menos de 5 % das cirurgias irão demandar tal quantidade de tempo. Observe a figura abaixo e conclua.

x  = seq(70,220,length.out = 200)
dx = dnorm(x,mean = 129, sd=14)
xdx = data.frame(x, dx)

ggplot(xdx, aes(x = x,y = dx)) + 
  geom_line() + 
  xlab("x") + 
  ylab("Densidade") +  
  ggtitle("N"~(mu==129~~sigma == 14)) +
  geom_vline(xintercept = 199, colour="red")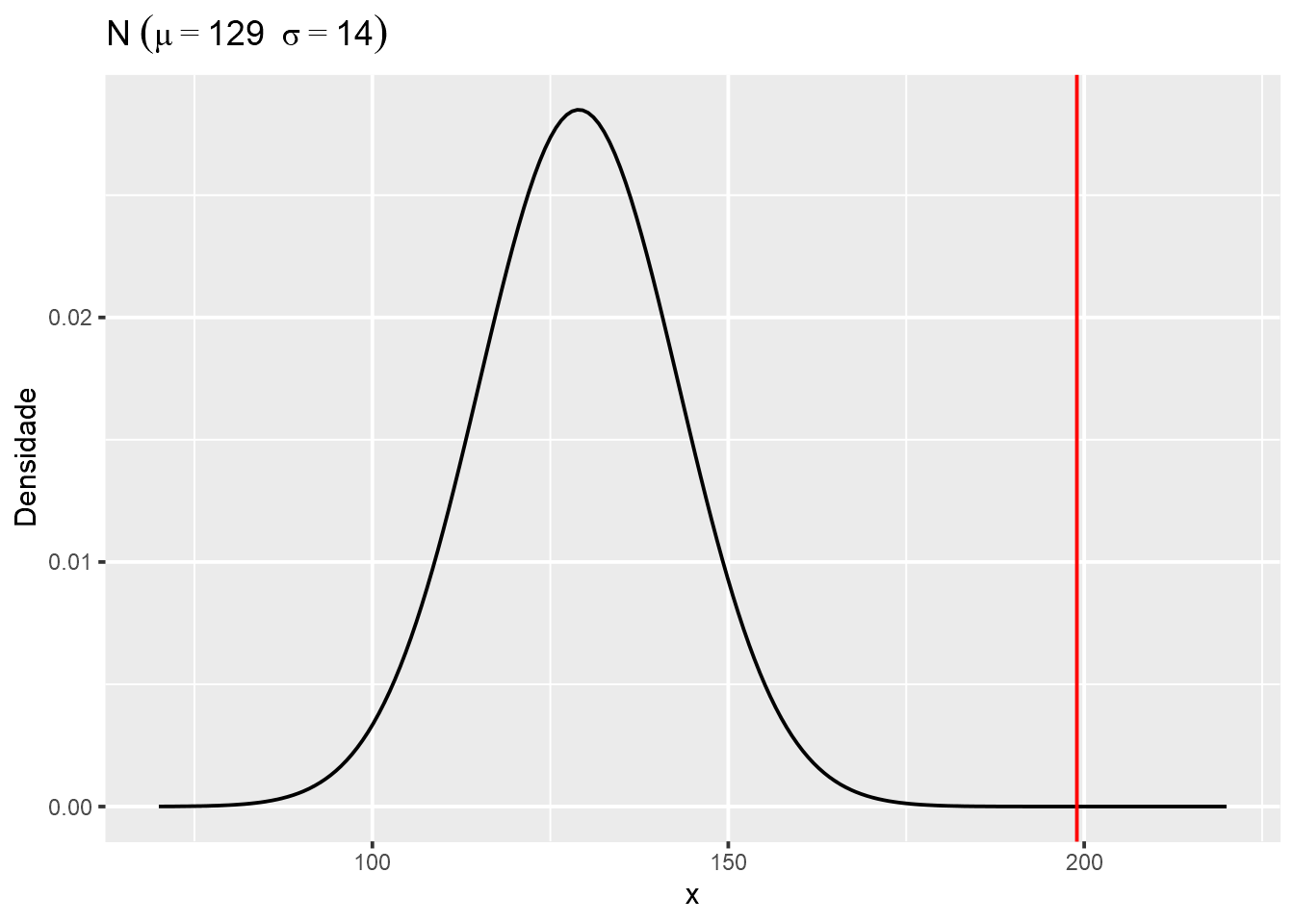

Exemplo - Normal 2

Numa ilha existem três modelos de automóveis disponíveis para compra, um de cada uma das seguintes marcas: A, B e C. Segundo os fabricantes, e tendo em conta as características da rede de estradas local, o consumo dos referidos automóveis (em litros aos cem km) é caracterizado pelas seguintes distribuições:

\(A \sim N(10,1^2)\)
\(B \sim N(11,1.5^2)\)
\(C \sim N(8,1.25^2)\)

Um determinado Senhor, residente da ilha, possui um automóvel da marca C, dois da marca A e três da marca B. O referido Senhor tem por costume escolher na segunda-feira de manhã o automóvel que vai utilizar ao longo da semana.

Sabendo que na última semana o automóvel utilizado gastou em média mais de 10 litros (aos cem km), calcule a probabilidade de ter sido um automóvel da marca A o escolhido.
Qual a probabilidade de o consumo de um automóvel da marca C ser pelo menos 1 litro inferior ao consumo de um automóvel da marca A?

Solução

a - Sabendo que na última semana o automóvel utilizado gastou em média mais de 10 litros (aos cem km), calcule a probabilidade de ter sido um automóvel da marca A o escolhido.

A questão pode ser respondida utilizando o teorema de Bayes. Imagine o espaço amostral particionado com eventos mutuamente exclusivos (carros), agora suponha o evento de interesse ocorrendo neste espaço amostral (\(X > 10\)), onde \(X = consumo\), v.a. contínua com distribuição normal. Podemos representar esse cenário (partições) de acordo com a figura abaixo e suas probabilidades.

\[ \mathbb{P}(A) = \frac{2}{6} \\ \mathbb{P}(B) = \frac{3}{6} \\ \mathbb{P}(C) = \frac{1}{6} \\ \]

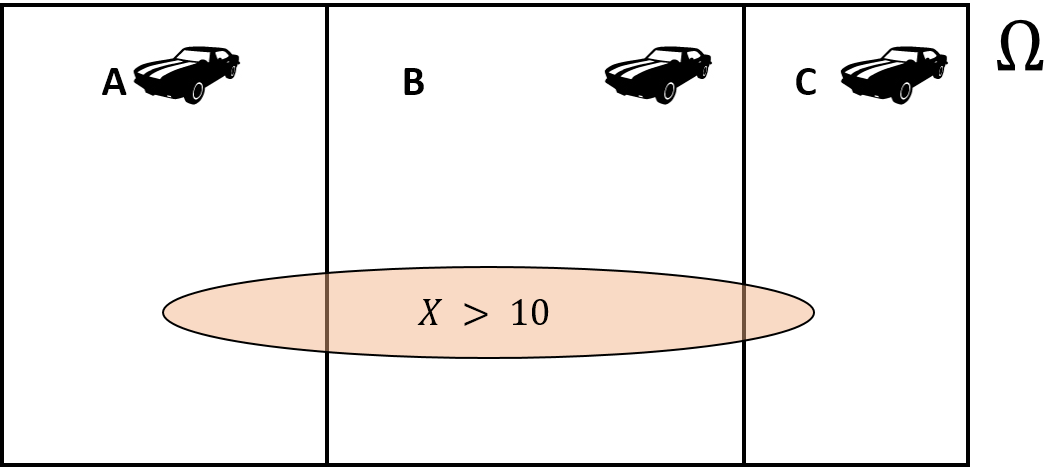
Dado que o consumo foi maior do que 10 litros/100 km, \(X > 10\), qual é a probabilidade de ter sido o carro A o escolhido, ou seja,

\[ \mathbb{P}(A | X > 10) = \frac{\mathbb{P}(A).\mathbb{P}(X > 10|A)}{\mathbb{P}(X > 10)} \\ \\ \mathbb{P}(A | X > 10) = \frac{\mathbb{P}(A).\mathbb{P}(X > 10|A)}{\mathbb{P}(A).\mathbb{P}(X > 10|A) + \mathbb{P}(B).\mathbb{P}(X > 10|B) +\mathbb{P}(C).\mathbb{P}(X > 10|C)} \\ \] Para calcularmos as probabilidades condicionais temos,

library(ggplot2)
ggplot(data.frame(x=c(0,20)),aes(x=x)) +
  stat_function(fun=dnorm,geom = "line",size=1,col="blue",args = c(mean=10,sd=1)) +
  stat_function(fun=dnorm,geom = "line",size=1,col="green",args = c(mean=11,sd=1.5)) +
  stat_function(fun=dnorm,geom = "line",size=1,col="red",args = c(mean=8,sd=1.25)) +
  geom_vline(xintercept = 10, colour="black") +
  scale_y_continuous(name = expression(f[X](x)))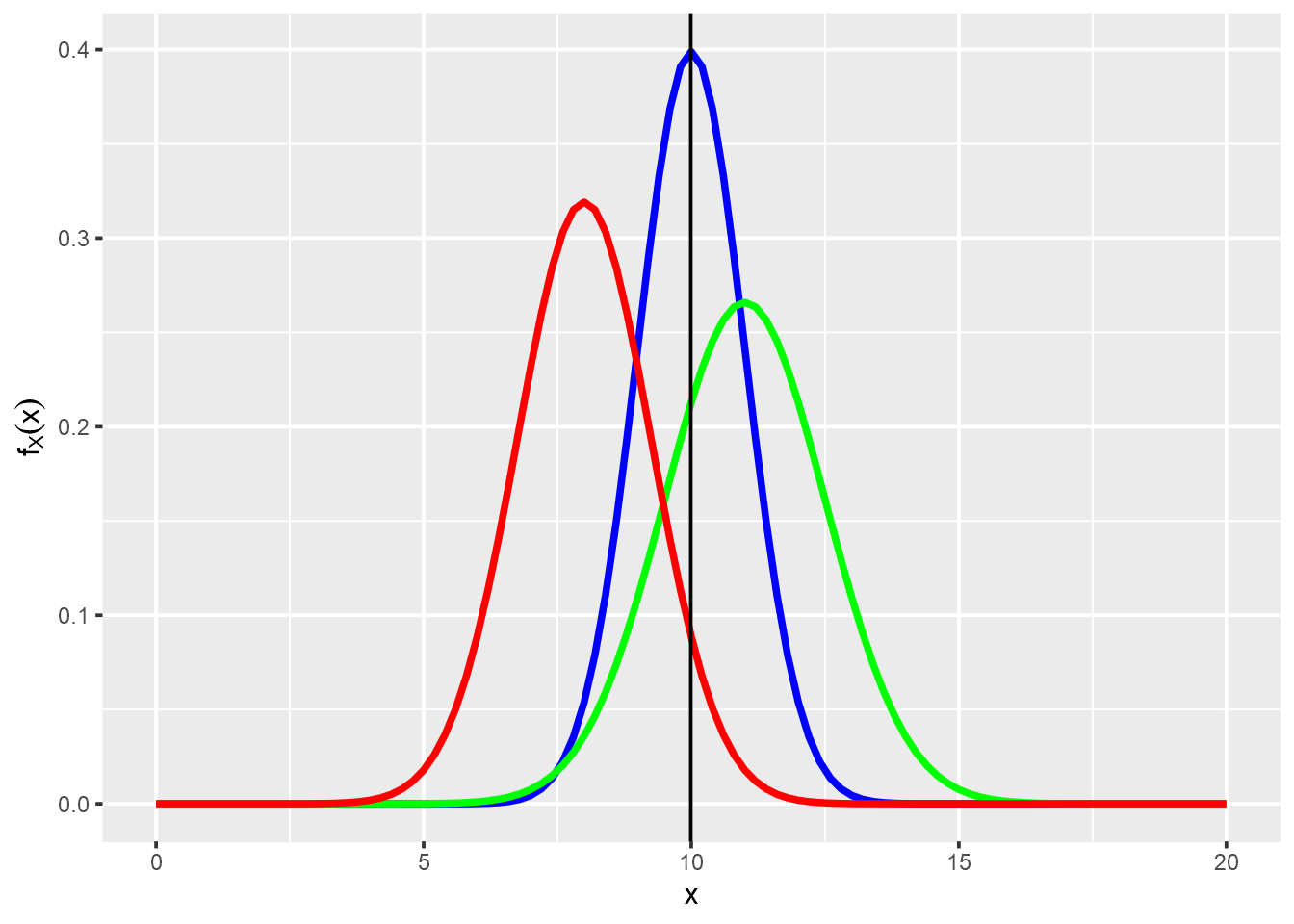

\[ \mathbb{P}(X > 10 | A) = 0.50\\ \] \[ \mathbb{P}(X > 10 | B) = 0.7475075\\ \] \[ \mathbb{P}(X > 10 | C) = 0.05479929\\ \]

mu_A = 10 # média A
sd_A = 1  # desvio padrão A 
mu_B = 11
sd_B = 1.5
mu_C = 8
sd_C = 1.25

# 1 - phi(x) = 1 - F(x) = 1 - função cumulativa normal
pxA = 1 - pnorm(10,mu_A,sd_A) 
pxB = 1 - pnorm(10,mu_B,sd_B)
pxC = 1 - pnorm(10,mu_C,sd_C)

# utilizando cat como print de var e texto.
cat("P(X>10|A) = ", pxA, "\n")

P(X>10|A) =  0.5

cat("P(X>10|B) = ", pxB, "\n")

P(X>10|B) =  0.7475075

cat("P(X>10|C) = ", pxC)

P(X>10|C) =  0.05479929

Assim temos que,

\[ \mathbb{P}(A | X > 10) = \frac{\mathbb{P}(A).\mathbb{P}(X > 10|A)}{\mathbb{P}(X > 10)} = \frac{(2/6)(0.5)}{(2/6)(0.5) + (3/6)(0.748)+(1/6)(0.0548)} = 0.303 \\ \] A probabilidade de ter sido escolhido o carro A, dado que \(X>10\) ocorreu é de \(0.303\) ou 30.3 %.

b - Qual a probabilidade de o consumo de um automóvel da marca C ser pelo menos 1 litro inferior ao consumo de um automóvel da marca A?

Nesta questão vamos que utilizar a distribuição da diferença entre variáveis aleatórias, ou seja a distribuição da diferença entre o consumo do carro C e A. Como consequência teremos uma nova distribuição normal, sendo C e A normais, e aplicaremos a propriedade da linearidade do valor esperado e da variância para determinar os parâmetros desta nova distribuição.

Assim temos que a nova variável aleatória é \(D\) onde,

\[ D = C - A \] Sabemos que \(D\) possui distribuição normal, com média e variância / desvio padrão.

Calculando os parâmetros,

\[ E[C - A] = E[C] - E[A] \\ V(C -A) = V(C) + V(A) \\ \] Substituindo,

\[ E[D] = E[C] - E[A] = 8 - 10 = -2 \\ V(D) = V(C) + V(A) = (1)^2 + (1.25)^2 = 2.5625 \\ DP(D) = 1.60 \\ \]

Dessa forma a distribuição da v.a. \(D\) representa a diferença no consumo do carro C em relação ao carro A.

library(ggplot2)
ggplot(data.frame(x=c(-8,4)),aes(x=x)) +
  stat_function(fun=dnorm,geom = "line",size=1,col="green",args = c(mean=-2,sd=1.60)) +
  scale_x_continuous(name = "d",breaks = seq(-8,4,2)) +
  scale_y_continuous(name = expression(f[D](d)))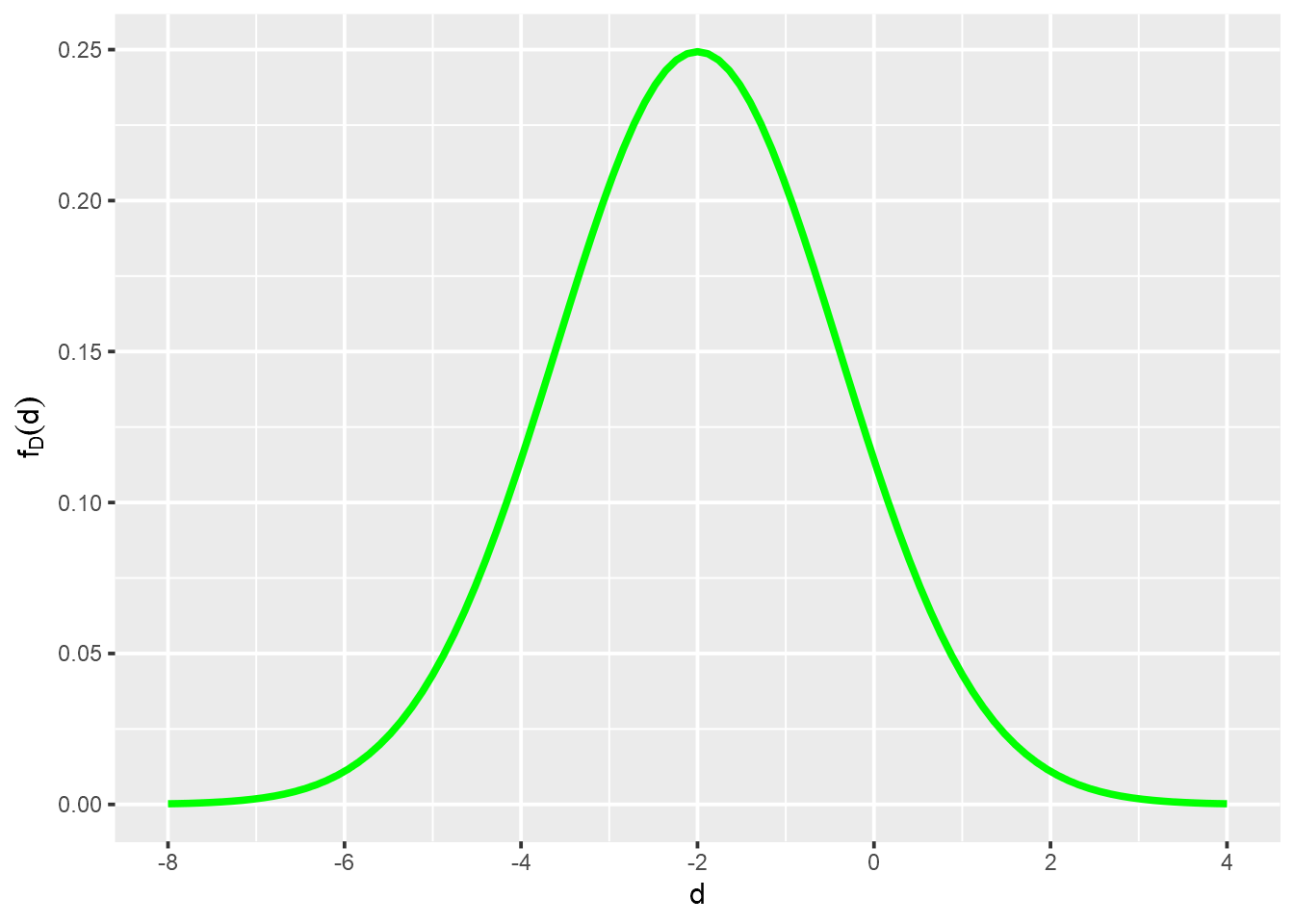

Para calcularmos a probabilidade de o consumo de um automóvel da marca C ser pelo menos 1 litro inferior ao consumo de um automóvel da marca A,

\[ \mathbb{P}(D < -1) = 0.7340145\\ \]

Intepretação:

Considere o seguinte,

se \(D = 0\) significa que o consumo dos dois automóveis C e A não se diferenciam
se \(D = 1\) significa que o consumo de C é 1 litro superior ao de A
se \(D = -1\) significa que o consumo de C é 1 litro inferior ao de A
na média o consumo de D é de 2 litros inferior ao de A (\(\mu = -2\))

Assim,

mu_D = -2 # média D
sd_D = 1.60  # desvio padrão D 

# phi(x) = F(x) = função cumulativa normal
pxD = pnorm(-1,mu_D,sd_D) 

# utilizando cat como print de var e texto.
cat("P(D < -1) = ", pxD, "\n")

P(D < -1) =  0.7340145

funcShaded <- function(x) {
    y <- dnorm(x, mean = -2, sd = 1.6)
    y[ x > -1] = NA
    return(y)
}

ggplot(data.frame(x=c(-8,4)),aes(x=x)) +
  stat_function(fun=dnorm,geom = "line",size=1,col="green",args = c(mean=-2,sd=1.60)) +
  stat_function(fun=funcShaded, geom="area", fill="#84CA72", alpha=0.2) +
  scale_x_continuous(name = "d",breaks = seq(-8,4,1)) +
  scale_y_continuous(name = expression(f[D](d)))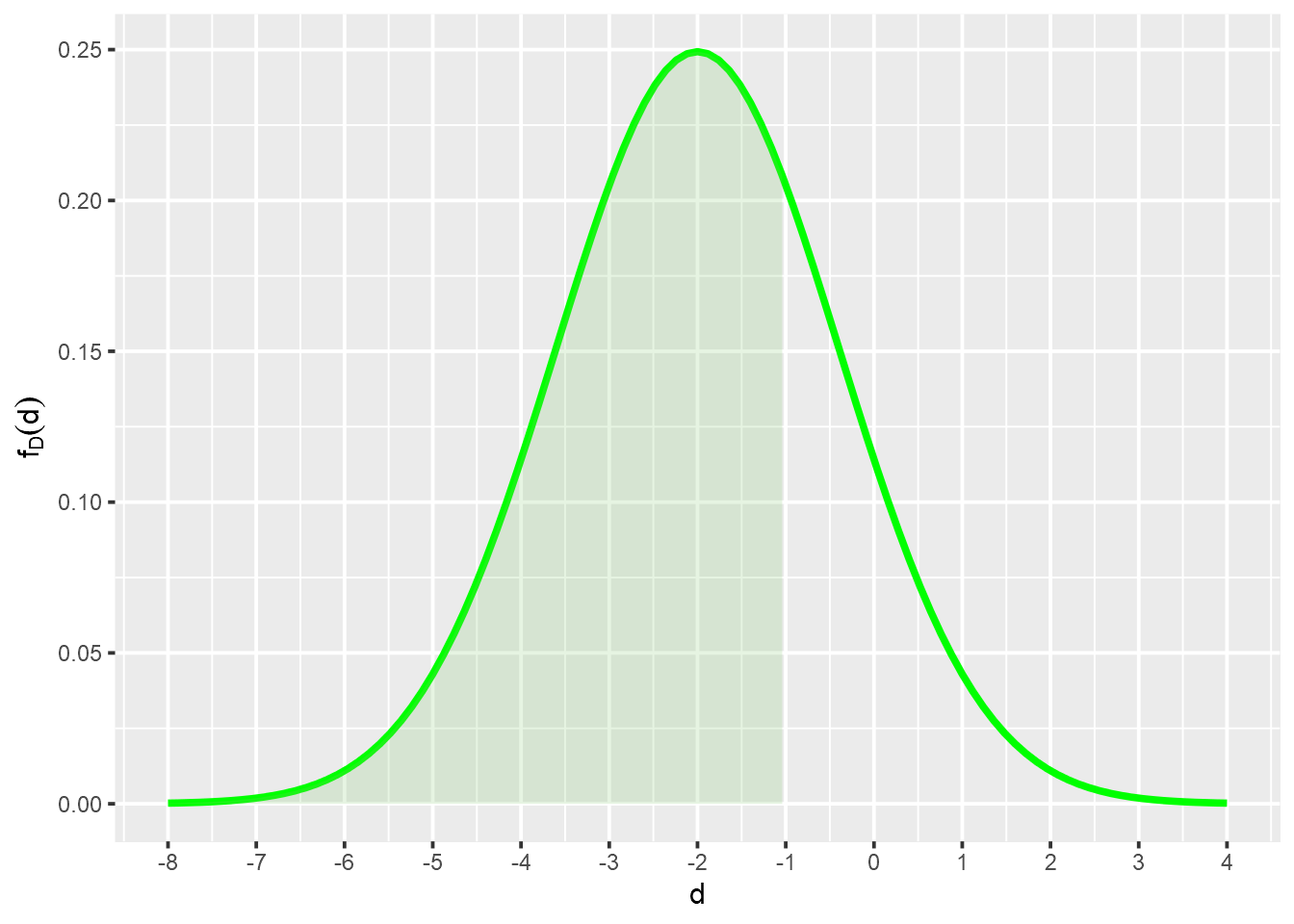

Este conteúdo está disponível por meio da Licença Creative Commons 4.0

Distribuição Normal (Gaussiana)