Em 1733 Abraham De Moivre representou um resultado extramente importante dentro da teoria da probabilidade que era a distribuição das médias extraídas de uma população tendem à uma distribuição normal, na medida em que mais réplicas desse experimento forem ocorrendo. No mesmo sentido, De Moivre verificou que a distribuição normal aproximava muito bem as probabilidades de uma variável aleatória binomial a medida em que \(n\) aumentava.

Tal aproximação se torna bastante útil na medida em que de fato \(n\) tende a aumentar, o que faz com seja extremamente tedioso o cálculo de fatoriais e combinações para tais casos. Dessa forma uma aproximação, ou forma simplificada de cálculo das probabilidades se faz necessário.

Imagine o caso em que se tenha \(n = 500\) repetições de um experimento, em que a probabilidade de sucesso é de \(p = 0.50\). Calcule a probabilidade do valor de \(350 < X < 478\). Na atualidade faríamos uso de um computador para tal cálculo.

Só para se ter uma ideia, o valor de uma combinação, de \(350\) sucessos em \(500\) tentativas é de:

choose(500,350)
[1] 1.727989e+131

Agora imagine realizar tal tarefa, calcular essa combinação, em 1733… Bem, até mesmo o cálculo do fatorial \(n!\) era complexo e demorado. Tanto que James Stirling desenvolveu uma equação para aproximar o fatorial, chamada de fórmula de Stirling:

\[ n! = \sqrt{2\pi n}\left(\frac{n}{e}\right)^n \]

Diante disso, o cálculo das probabilidades de uma v.a. binomial pode ser aproximado pela distribuição normal, no mesmo sentido outras distribuições discretas que dependendo dos seus parâmetros resultarem em uma forma simétrica, podem também, serem aproximadas por essa mesma distribuição.

Para isso algumas restrições são necessárias, para a aproximação seja feita de forma acurada.

Aproximação da Distribuição Binomial pela Distribuição Normal

A aproximação da distribuição binomial pela normal é realizada calculando os parâmetros que descrevem uma variável aleatória, como valor esperado ou média \(E[X]\) e variância \(V(X)\).

Assim temos que,

Valor Esperado e Variância de uma v.a. Binomial
\[ E[X] = \mu = np\\ V(X) = \sigma^2 = np(1-p) \]

Observe o seguinte, onde temos uma v.a. binomial com \(n=10\) e \(p=0.5\)

library(ggplot2)
library(grid)

n = 10
p = 0.5
x  = seq(0,n,1)
px = dbinom(x, n, p)
dat = data.frame(x, px)
# Aproximação
media = n*p # media
desvp = sqrt(n*p*(1-p)) # desvio padrao

ggplot(dat, aes(x = x, y = px)) + 
  geom_bar(stat = "identity", col = "pink", fill = "pink") + 
  geom_point(aes(x = x, y = px), colour = "black", size = 4) +
  scale_y_continuous(expand = c(0.01, 0)) + 
  xlab("x") + 
  ylab("px e fx") +
  stat_function(aes(x=x),fun=dnorm,geom = "line",size=1,col="green",args = c(mean = media, sd = desvp))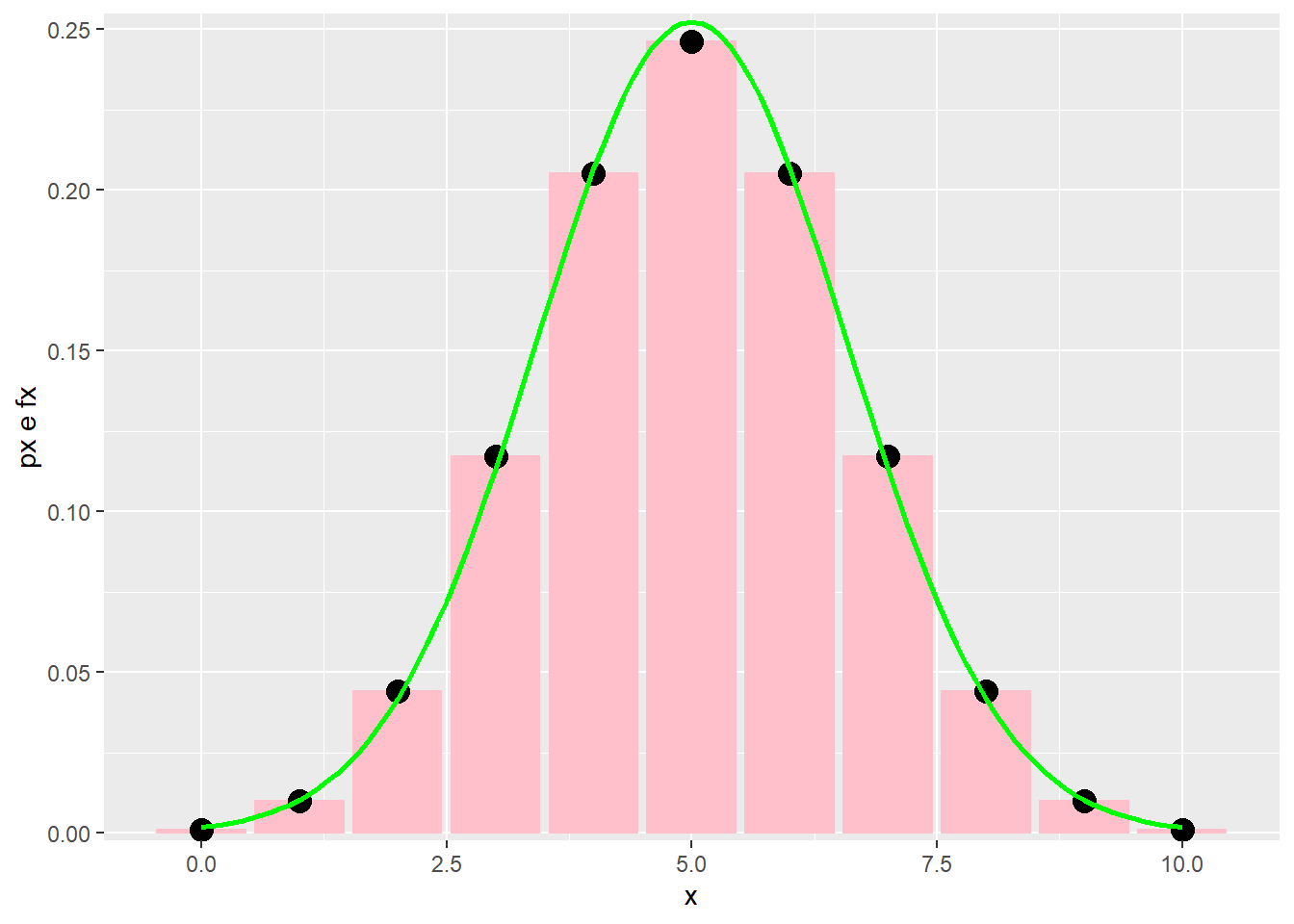

Como aproximação da normal temos,

\[ E[X] = \mu = np = 5\\ V(X) = \sigma^2 = np(1-p) = 1.58 \] Outras situações em que a aproximação resultante não é muito boa, exemplo:

\[ n=10\\ p=0.1 \]

require(ggplot2)
require(grid)

n = 10
p = 0.1
x  = seq(0,n,1)
px = dbinom(x, n, p)
dat = data.frame(x, px)
# Aproximação
media = n*p # media
desvp = sqrt(n*p*(1-p)) # desvio padrao

ggplot(dat, aes(x = x, y = px)) + 
  geom_bar(stat = "identity", col = "pink", fill = "pink") + 
  geom_point(aes(x = x, y = px), colour = "black", size = 4) +
  scale_y_continuous(expand = c(0.01, 0)) + 
  xlab("x") + 
  ylab("px e fx") +
  stat_function(aes(x=x),fun=dnorm,geom = "line",size=1,col="green",args = c(mean = media, sd = desvp))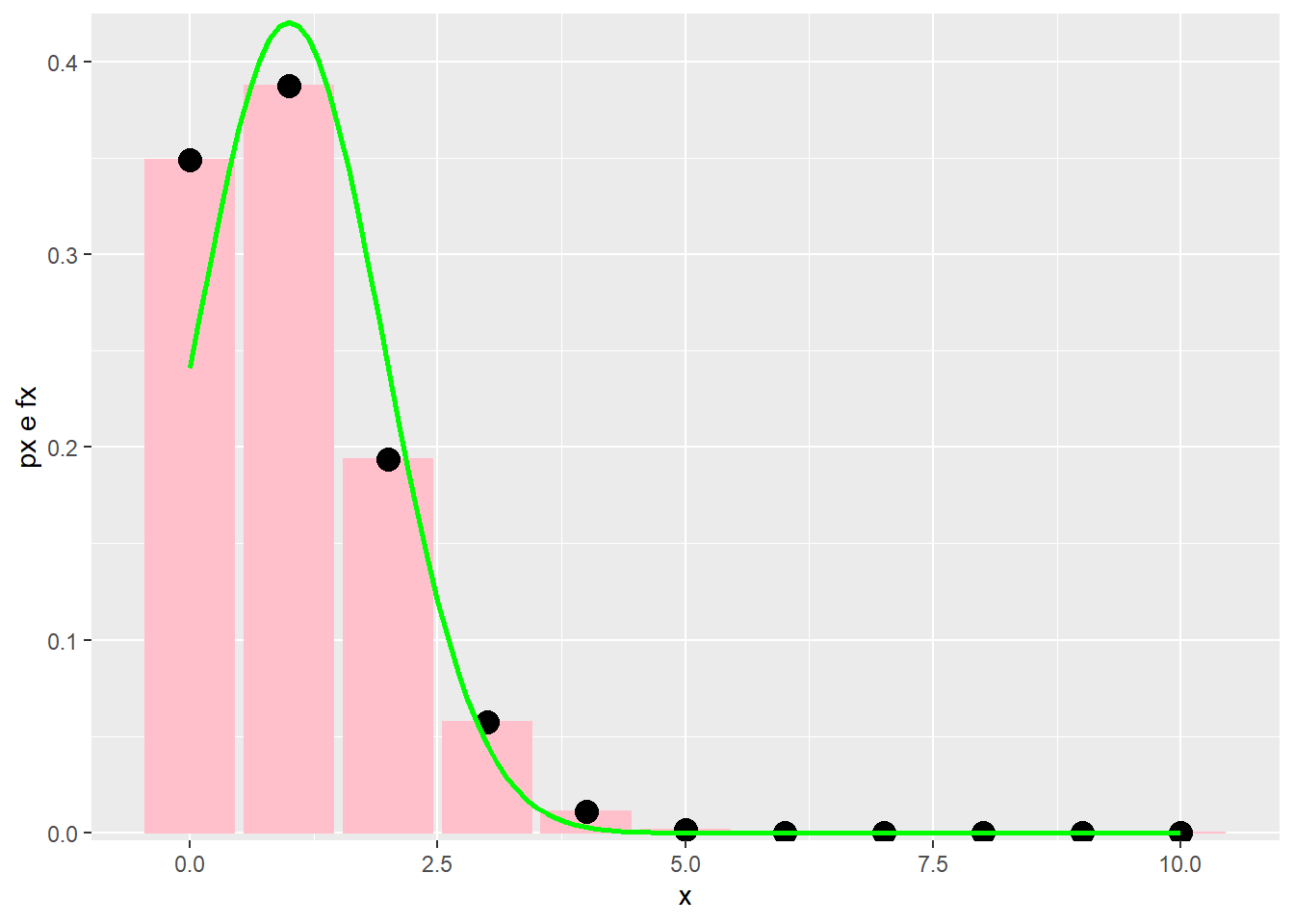

\[ n=10\\ p=0.9 \]

require(ggplot2)
require(grid)

n = 10
p = 0.9
x  = seq(0,n,1)
px = dbinom(x, n, p)
dat = data.frame(x, px)
# Aproximação
media = n*p # media
desvp = sqrt(n*p*(1-p)) # desvio padrao

ggplot(dat, aes(x = x, y = px)) + 
  geom_bar(stat = "identity", col = "pink", fill = "pink") + 
  geom_point(aes(x = x, y = px), colour = "black", size = 4) +
  scale_y_continuous(expand = c(0.01, 0)) + 
  xlab("x") + 
  ylab("px e fx") +
  stat_function(aes(x=x),fun=dnorm,geom = "line",size=1,col="green",args = c(mean = media, sd = desvp))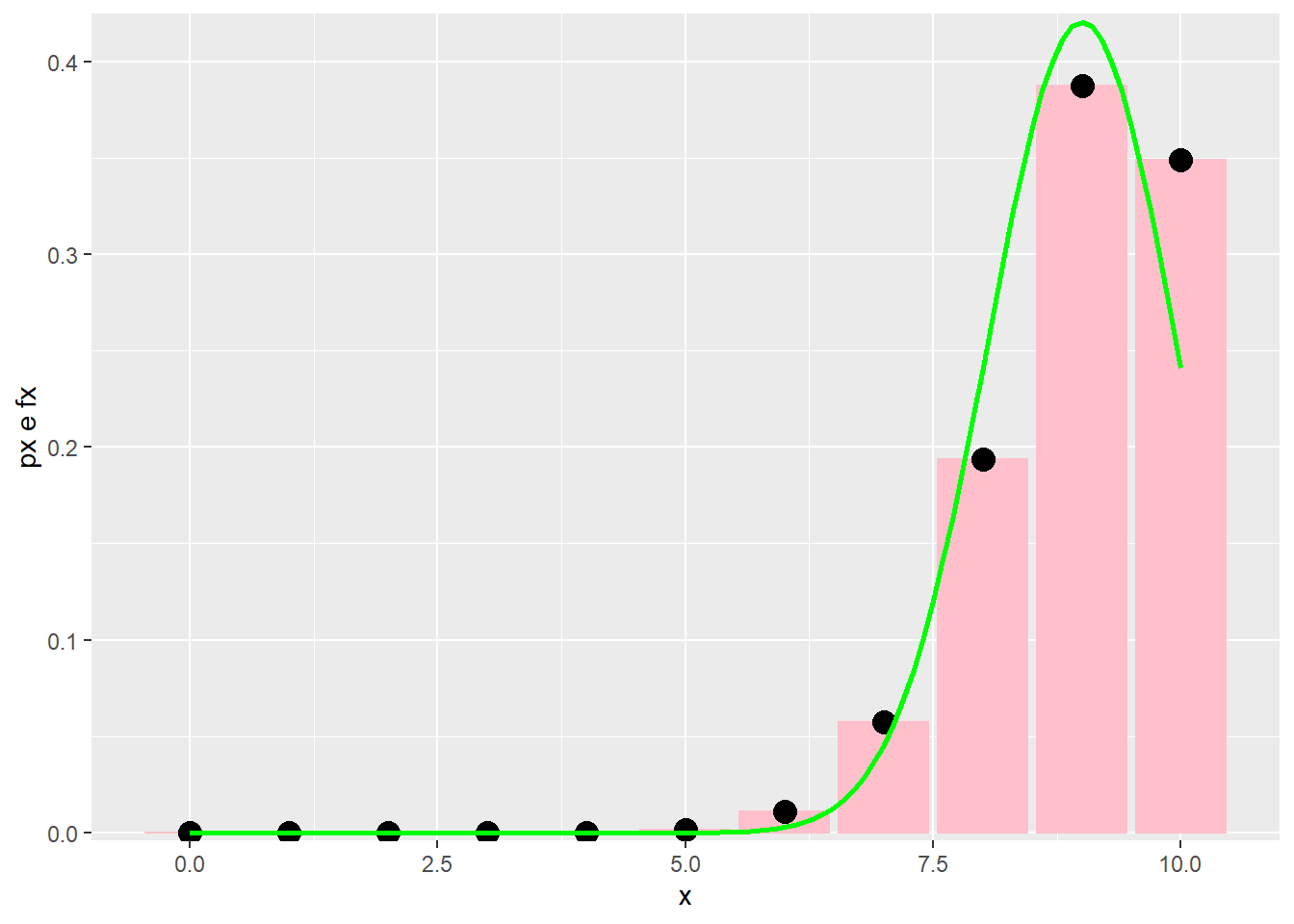

Situações em que a aproximação é boa
A aproximação será boa quando: \[ np > 5\\ ou \\ n(1-p) > 5 \]

Aproximação da Distribuição Poisson pela Distribuição Normal

Da mesma forma que é possível aproximar a distribuição de Poisson pela distribuição Normal, para isso os parâmetros da normal são,

Valor Esperado e Variância de uma v.a. Poisson
\[ E[X] = \mu = \lambda\\ V(X) = \sigma^2 = \lambda \]

No caso dessa aproximação é necessária outra restrição, no caso, a aproximação será boa quando,

Situações em que a aproximação da Poisson pela normal é boa
A aproximação será boa quando: \[ \lambda > 5 \]

Exemplos:

\[ \lambda = 5 \]

require(ggplot2)
require(grid)

lambda = 5
n = 30 # tende ao infinito

x  = seq(0,n,1)
px = dpois(x, lambda)
dat = data.frame(x, px)

# Aproximação
media = lambda # media
desvp = sqrt(lambda) # desvio padrao

ggplot(dat, aes(x = x, y = px)) + 
  geom_bar(stat = "identity", col = "pink", fill = "pink") + 
  geom_point(aes(x = x, y = px), colour = "black", size = 4) +
  scale_y_continuous(expand = c(0.01, 0)) + 
  xlab("x") + 
  ylab("px e fx") +
  stat_function(aes(x=x),fun=dnorm,geom = "line",size=1,col="green",args = c(mean = media, sd = desvp))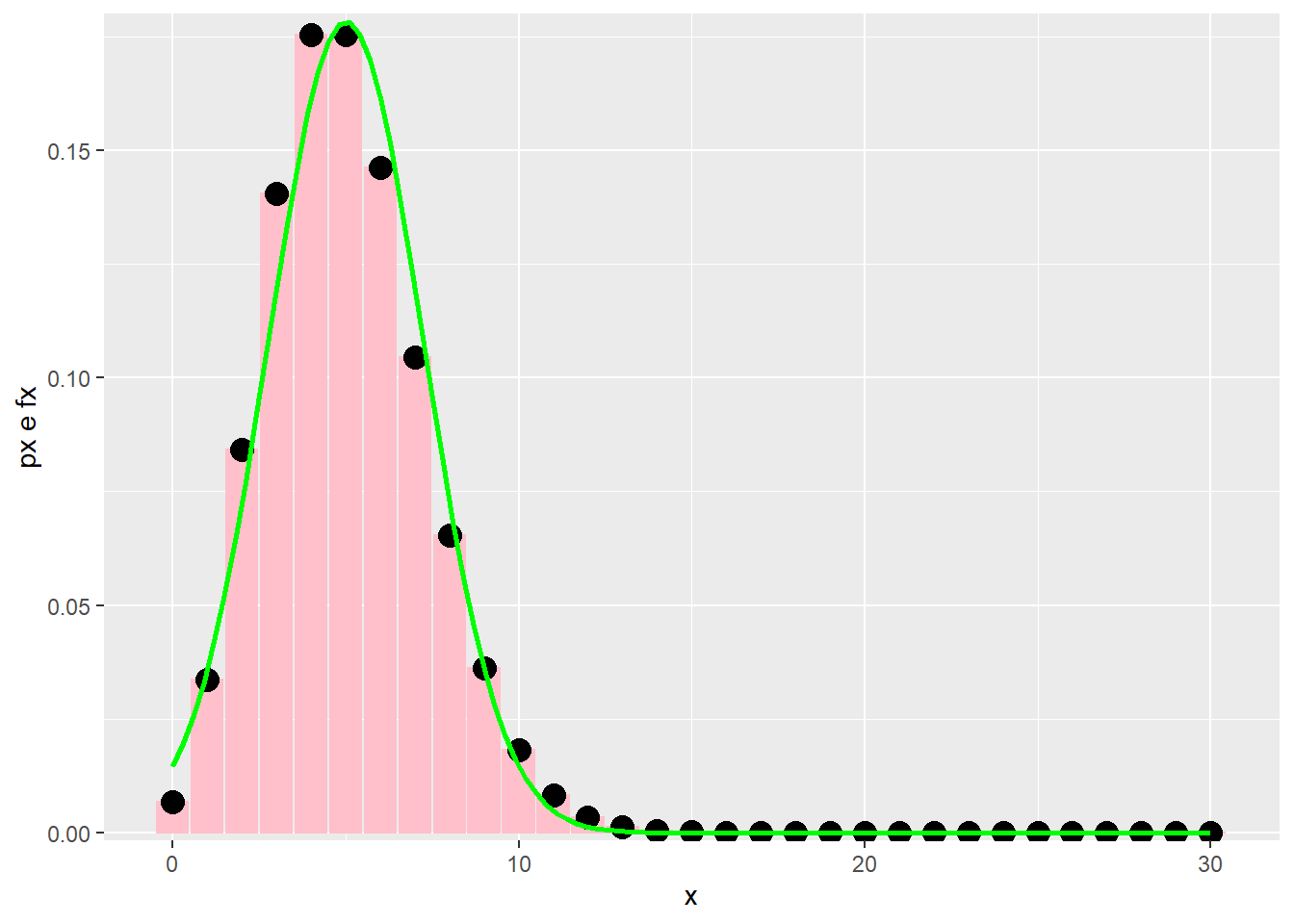

\[ \lambda = 8 \]

require(ggplot2)
require(grid)

lambda = 8
n = 30 # tende ao infinito

x  = seq(0,n,1)
px = dpois(x, lambda)
dat = data.frame(x, px)

# Aproximação
media = lambda # media
desvp = sqrt(lambda) # desvio padrao

ggplot(dat, aes(x = x, y = px)) + 
  geom_bar(stat = "identity", col = "pink", fill = "pink") + 
  geom_point(aes(x = x, y = px), colour = "black", size = 4) +
  scale_y_continuous(expand = c(0.01, 0)) + 
  xlab("x") + 
  ylab("px e fx") +
  stat_function(aes(x=x),fun=dnorm,geom = "line",size=1,col="green",args = c(mean = media, sd = desvp))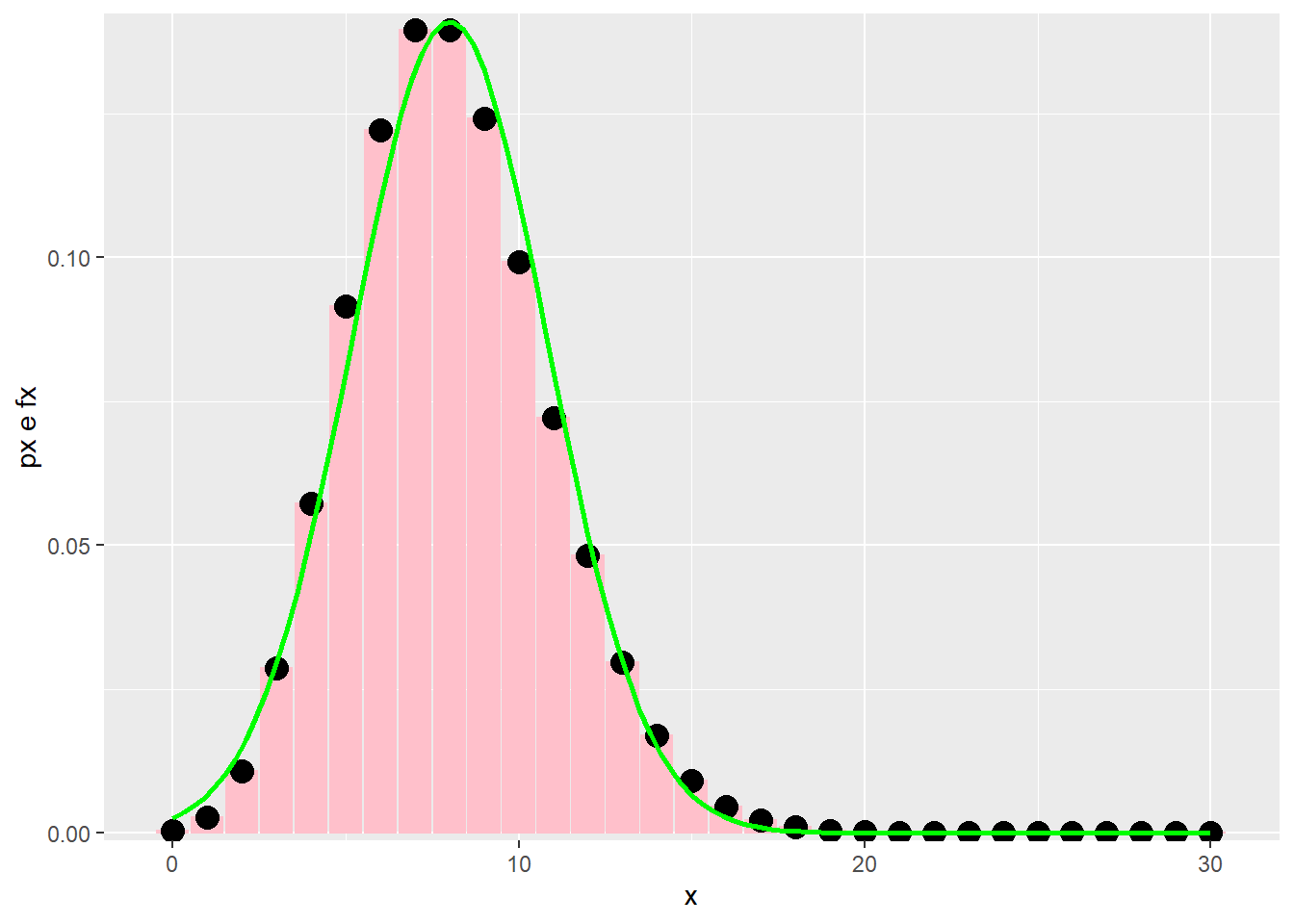

Situação em que a aproximação não é boa,

\[ \lambda = 2 \]

library(ggplot2)
library(grid)

lambda = 2
n = 30 # tende ao infinito

x  = seq(0,n,1)
px = dpois(x, lambda)
dat = data.frame(x, px)

# Aproximação
media = lambda # media
desvp = sqrt(lambda) # desvio padrao

ggplot(dat, aes(x = x, y = px)) + 
  geom_bar(stat = "identity", col = "pink", fill = "pink") + 
  geom_point(aes(x = x, y = px), colour = "black", size = 4) +
  scale_y_continuous(expand = c(0.01, 0)) + 
  xlab("x") + 
  ylab("px e fx") +
  stat_function(aes(x=x),fun=dnorm,geom = "line",size=1,col="green",args = c(mean = media, sd = desvp))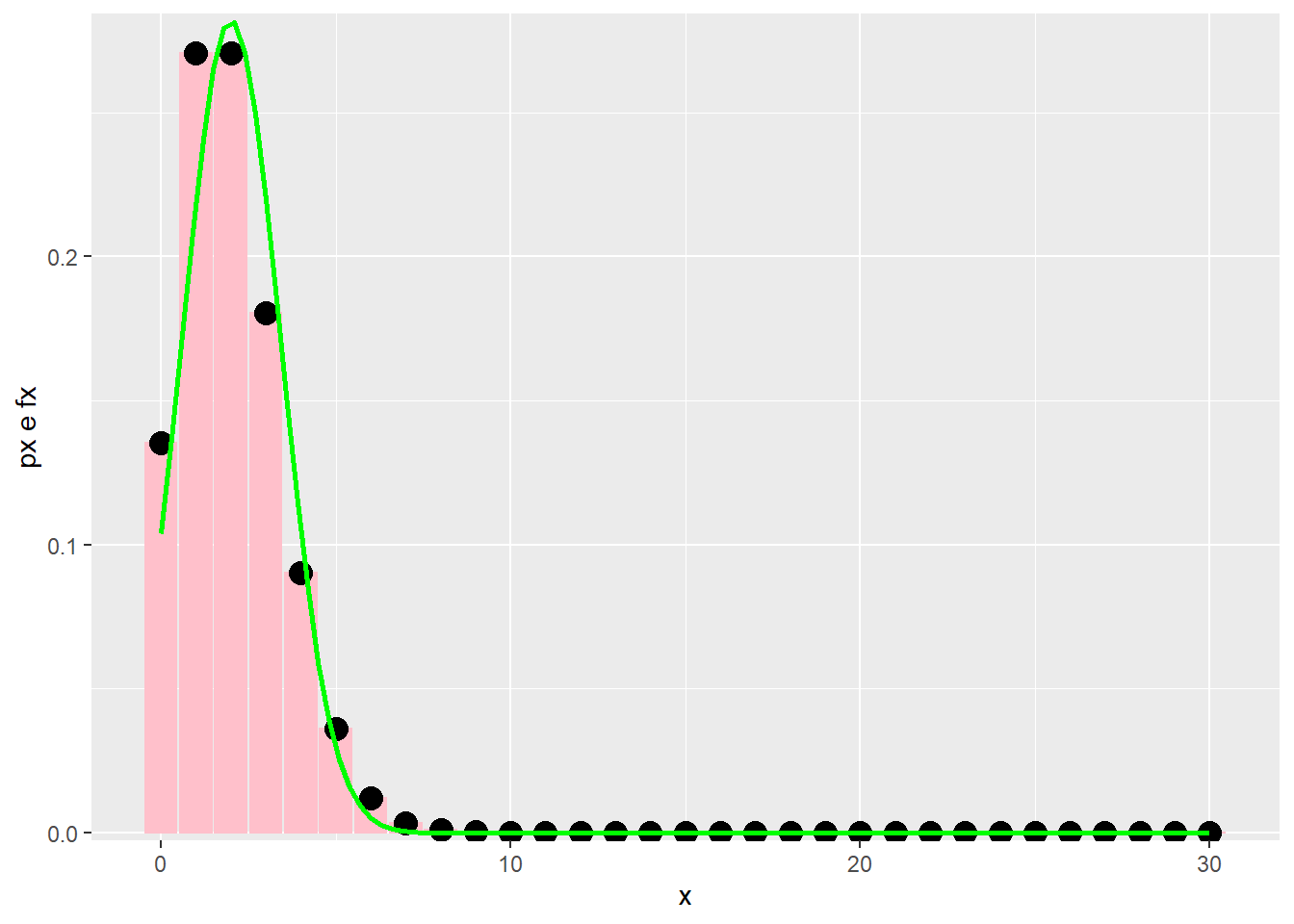

Calculando as probabilidades e correção da continuidade

Para se calcular as probabilidades de uma distribuição discreta utilizando uma distribuição contínua é necessário realizar a correção da continuidade. Para facilitar o entendimento observe os exemplos gráficos abaixo.

Suponha que se tenha interesse em calcular a probabilidade de \(3 \le X \le 5\), ou seja \(\mathbb{P}(3 \le X \le 5)\), deve se recorrer à correção da continuidade, adicionado e removendo \(0.5\) do valor da v.a. \(X\), neste caso, calculando pela distribuição contínua \(\mathbb{P}(2.5 \le X \le 5.5)\).

Licença Creative Commons 4.0

Este conteúdo está disponível por meio da Licença Creative Commons 4.0