Cadeias de Markov
Introdução
Neste tópico vamos introduzir as cadeias de Markov, que são processos aleatórios que satisfazem a propriedade de Markov. Nomeado por Andrey Markov, talvez o membro mais conhecido de uma família de famosos matemáticos russos do final do século XIX ao início do século XX.
Um processo aleatório que satisfaz a propriedade Markov possui a seguinte característica interessante. Pode-se fazer previsões em seu futuro com base somente em seu estado atual independentemente do que aconteceu no passado até esse estado atual. Em outras palavras, condicional ao estado atual do processo, suas evoluções futuras e passadas são independentes. Como tal, as cadeias de Markov são bastante gerais e desfrutam de uma ampla gama De aplicações.
Nestes tópicos abordaremos as cadeias de Markov, uma classe geral de processo estocástico (aleatórios) com muitas aplicações que lidam com a evolução de sistemas dinâmicos. Ao contrário dos processos de Bernoulli e Poisson, que são sem memória, no sentido de que o futuro não depende do passado. Já as cadeias de Markov são mais elaboradas, pois permitem alguma dependências entre diferentes períodos de tempo.
No entanto, essas dependências são de natureza simples e restrita, capturadas pela chamada propriedade de Markov. Condicionada ao estado atual da cadeia de Markov, suas evoluções futuras e passadas são independentes. Conforme mencionado na visão geral da unidade, consideramos apenas cadeias de Markov de tempo discreto que evoluem em espaços de estados finitos. Isso nos permite concentrar-nos nos principais conceitos sem ter que lidar com alguns detalhes técnicos necessários necessários para estudar os processos gerais de Markov em tempo contínuo e espaços de estado gerais, possivelmente incontáveis.
Definição
Se tivermos uma sequência de variáveis aleatórias \(X_1,X_2, ...X_n\) onde os índices \(1 ,2 ,... ,n\) representar pontos sucessivos no tempo, podemos usar a regra da cadeia de probabilidade para calcular a probabilidade de toda a sequência:
\[ p(X_1, X_2, \ldots X_n) = p(X_1) \cdot p(X_2 | X_1) \cdot p(X_3 | X_2, X_1) \cdot \ldots \cdot p(X_n | X_{n-1}, X_{n-2}, \ldots, X_2, X_1) \, . \]
As cadeias de Markov simplificam essa expressão usando a suposição de Markov . A suposição é que, dado todo o histórico anterior, a distribuição de probabilidade para a variável aleatória na próxima etapa de tempo depende apenas da variável atual. Matematicamente, a suposição é escrita assim:
\[ p(X_{t+1} | X_t, X_{t-1}, \ldots, X_2, X_1 ) = p(X_{t+1} | X_t) \, \]
para todos \(t = 2 , ... , n\). Partindo desse pressuposto, podemos escrever a primeira expressão como
\[ p(X_1, X_2, \ldots X_n) = p(X_1) \cdot p(X_2 | X_1) \cdot p(X_3 | X_2) \cdot p(X_4 | X_3) \cdot \ldots \cdot p(X_n | X_{n-1}) \, \]
que é muito mais simples do que o original. Consiste em uma distribuição inicial para a primeira variável, \(p(X1)\), e \(n - 1\) probabilidades de transição. Normalmente fazemos mais uma suposição: que as probabilidades de transição não mudam com o tempo. Portanto, a transição do tempot para o tempo \(t + 1\) depende apenas do valor de \(X_t\).
Exemplos de cadeias de Markov
Cadeia discreta de Markov
Suponha que você tenha um número secreto (torne-o um inteiro) entre 1 e 5. Vamos chamá-lo de seu número inicial na etapa 1. Agora, para cada etapa de tempo, seu número secreto mudará de acordo com as seguintes regras:
- Jogue uma moeda.
- Se a moeda der cara, aumente o seu número secreto em um (5 aumenta para 1).
- Se a moeda der coroa, diminua seu número secreto em um (1 diminui para 5).
- Repetir n vezes e registre a história em evolução de seu número secreto.
Antes do experimento, podemos pensar na sequência de números secretos como uma sequência de variáveis aleatórias, cada uma assumindo um valor em \(\{ 1 , 2 , 3 , 4 , 5 \}\). Suponha que a moeda seja justa, de modo que, a cada lance, a probabilidade de cara e coroa seja de \(0.5\).
Este jogo se qualifica como uma verdadeira cadeia de Markov? Suponha que seu número secreto seja atualmente 4 e que o histórico de seus números secretos seja \((2, 1 , 2 , 3 )\). Qual é a probabilidade de que, na próxima etapa, seu número secreto seja \(5\)? E quanto às outras quatro possibilidades? Por causa das regras deste jogo, a probabilidade da próxima transição dependerá apenas do fato de que seu número atual é \(4\). Os números mais antigos de seu histórico são irrelevantes, então esta é uma cadeia de Markov.
Este é um exemplo de uma cadeia de Markov discreta, onde os valores possíveis das variáveis aleatórias vêm de um conjunto discreto. Esses valores possíveis (números secretos neste exemplo) são chamados de estados da cadeia. Os estados geralmente são números, como neste exemplo, mas podem representar qualquer coisa. Em um outro exemplo, os estados descrevem o clima em um determinado dia, que pode ser rotulado como 1 - bom, 2 - ruim.
Caminhada aleatória (random walk) - estado contínuo
Agora vamos dar uma olhada em um exemplo contínuo de uma cadeia de Markov. Dizer \(X_t= 0\) e temos o seguinte modelo de transição: \(p(X_{t + 1}|X_t=x_t) = N (x_t, 1 )\). Ou seja, a distribuição de probabilidade para o próximo estado é uma Normal com variância \(1\) e média (valor esperado) igual ao estado atual. Isso costuma ser chamado de “caminhada aleatória”. Claramente, é uma cadeia de Markov porque a transição para o próximo estado \(X_{t + 1}\) só depende do estado atual \(X_t\).
Este é exemplo simples para implementarmos em R:
n = 100
x = numeric(n)
for (i in 2:n) {
x[i] = rnorm(1, mean=x[i-1], sd=1.0)
}
#plot.ts(x)
plot(x, type = "l", xlab = "tempo")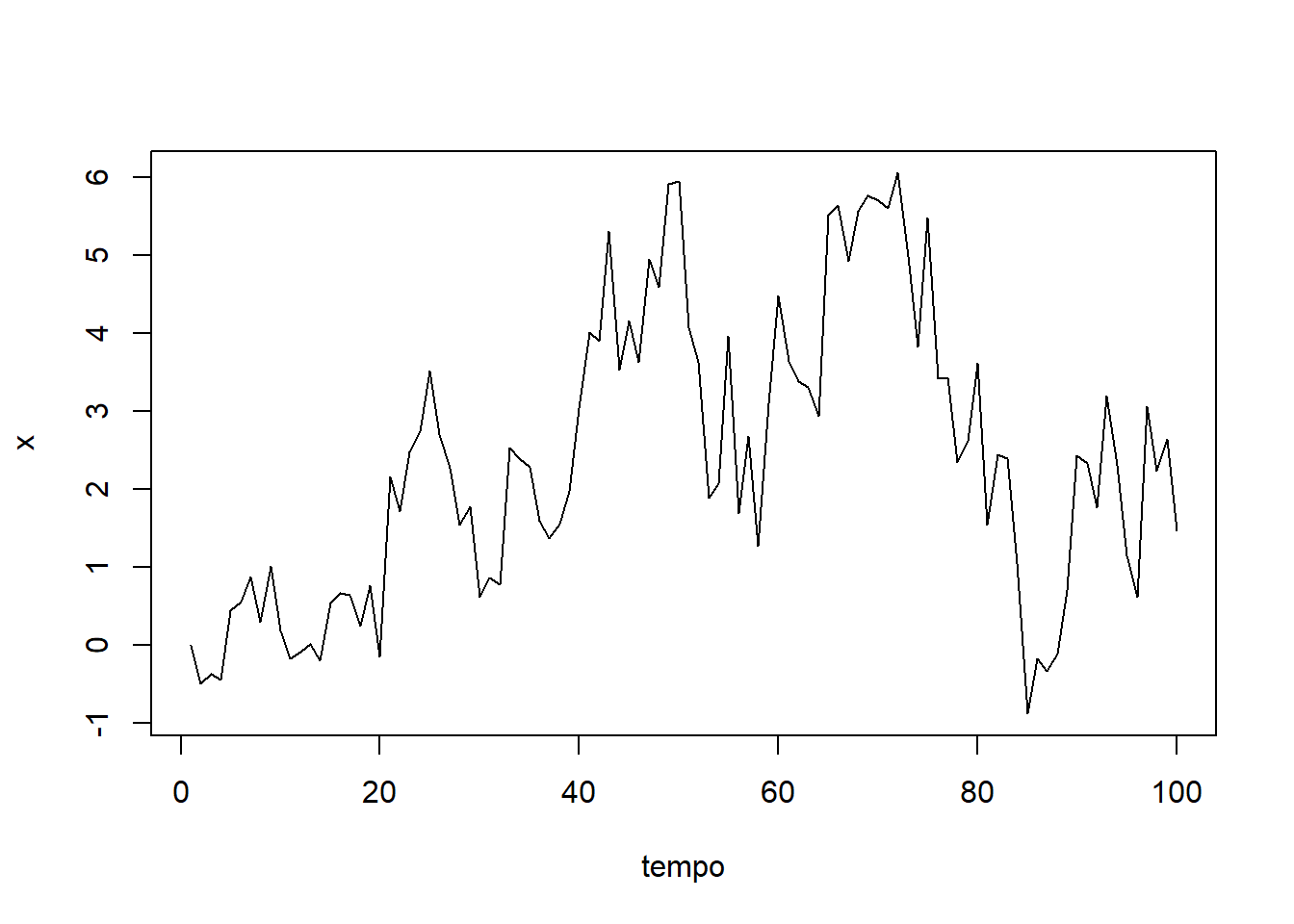
Matriz de transição
Voltemos ao nosso exemplo da cadeia de Markov de estado discreto. Se assumirmos que as probabilidades de transição não mudam com o tempo, então há um total de \(25(5^2)\) potenciais probabilidades de transição. As potenciais probabilidades de transição seriam do estado \(1\) para o estado \(2\), do estado \(1\) para o estado \(3\) e assim por diante. Essas probabilidades de transição podem ser organizadas em uma matriz que chamaremos de \(Q\):
\[ Q = \begin{pmatrix} 0 & .5 & 0 & 0 & .5 \\ .5 & 0 & .5 & 0 & 0 \\ 0 & .5 & 0 & .5 & 0 \\ 0 & 0 & .5 & 0 & .5 \\ .5 & 0 & 0 & .5 & 0 \\ \end{pmatrix} \]
onde as transições do Estado \(1\) estão na primeira linha, ex: probabilidade de se manter no estado \(1\) em um passo de tempo, \(p_{11}=0\), probabilidade de sair do estado \(1\) para o \(2\) em um passo de tempo, \(p_{12}=0.5\). As transições do Estado \(2\) estão na segunda linha, etc. Por exemplo, a probabilidade \(p_{15} = p(X_{t + 1} = 5| X_t = 4) = 0.5\) pode ser encontrada na quarta linha, quinta coluna.
A matriz de transição é especialmente útil se quisermos encontrar as probabilidades associadas a várias etapas da cadeia. Por exemplo, podemos querer saber \(p(X_{t + 2} = 3 | X_t = 1)\), a probabilidade de seu número secreto ser de \(3\) em duas etapas a partir de agora, dado que seu número atualmente é \(1\). Podemos calcular isso como
\[ \sum_{k=1}^5 p(X_{t+2}=3 \mid X_{t+1}=k) \cdot p(X_{t+1}=k \mid X_t=1) \] que se encontra convenientemente na primeira linha e na terceira coluna de \(Q^2\).
Podemos realizar essa multiplicação de matriz facilmente em R:
Q = matrix(c(0.0, 0.5, 0.0, 0.0, 0.5,
0.5, 0.0, 0.5, 0.0, 0.0,
0.0, 0.5, 0.0, 0.5, 0.0,
0.0, 0.0, 0.5, 0.0, 0.5,
0.5, 0.0, 0.0, 0.5, 0.0),
nrow=5, byrow=TRUE)
Q %*% Q # operador % para multiplicação de matrizes em R, = Q^2. [,1] [,2] [,3] [,4] [,5]
[1,] 0.50 0.00 0.25 0.25 0.00
[2,] 0.00 0.50 0.00 0.25 0.25
[3,] 0.25 0.00 0.50 0.00 0.25
[4,] 0.25 0.25 0.00 0.50 0.00
[5,] 0.00 0.25 0.25 0.00 0.50(Q %*% Q)[1,3][1] 0.25Portanto, se o seu número secreto for atualmente 1, a probabilidade de que o número seja 3 em duas etapas a partir de agora é 0.25.
\(p(X_{t + 2} = 3 | X_t = 1) = 0.25\)
Distribuição estacionária
Suponha que queremos saber a distribuição de probabilidade do seu número secreto em um futuro distante, digamos \(p(X_{t + h} | X_t)\). Onde \(h\) é um grande número. Vamos calcular isso para alguns valores diferentes de \(h\).
\(h = 5\) passos futuros
Q5 = Q %*% Q %*% Q %*% Q %*% Q # h = 5 passos futuros
round(Q5, 3) [,1] [,2] [,3] [,4] [,5]
[1,] 0.062 0.312 0.156 0.156 0.312
[2,] 0.312 0.062 0.312 0.156 0.156
[3,] 0.156 0.312 0.062 0.312 0.156
[4,] 0.156 0.156 0.312 0.062 0.312
[5,] 0.312 0.156 0.156 0.312 0.062\(h = 10\) passos futuros
Q10 = Q %*% Q %*% Q %*% Q %*% Q %*% Q %*% Q %*% Q %*% Q %*% Q # h = 10 passos futuros
round(Q10, 3) [,1] [,2] [,3] [,4] [,5]
[1,] 0.248 0.161 0.215 0.215 0.161
[2,] 0.161 0.248 0.161 0.215 0.215
[3,] 0.215 0.161 0.248 0.161 0.215
[4,] 0.215 0.215 0.161 0.248 0.161
[5,] 0.161 0.215 0.215 0.161 0.248\(h = 50\) passos futuros
Q50 = Q
for (i in 2:50) {
Q50 = Q50 %*% Q
}
round(Q50, 3) # h=30 steps in the future [,1] [,2] [,3] [,4] [,5]
[1,] 0.2 0.2 0.2 0.2 0.2
[2,] 0.2 0.2 0.2 0.2 0.2
[3,] 0.2 0.2 0.2 0.2 0.2
[4,] 0.2 0.2 0.2 0.2 0.2
[5,] 0.2 0.2 0.2 0.2 0.2Observe que, à medida que o horizonte futuro fica mais distante (\(h \rightarrow \infty\)), as distribuições de transição parecem convergir. O estado em que você se encontra torna-se menos importante na determinação de um futuro mais distante. Se deixarmos \(h\) ficar realmente grande e levarmos ao limite, todas as linhas da matriz de transição de longo prazo se tornarão iguais a \(( 0.2 , 0.2 , 0.2 , 0.2 , 0.2 )\). Ou seja, se você executar a cadeia de Markov por um longo tempo, a probabilidade de você acabar em qualquer estado particular é de \(1 / 5 = 0.2\) para cada um dos cinco estados. Essas probabilidades de longo prazo são iguais ao que é chamado de distribuição estacionária da cadeia de Markov.
A distribuição estacionária de uma cadeia é a distribuição de estado inicial para a qual realizar uma transição não mudará a probabilidade de terminar em qualquer estado dado. Isso é,
\[ [\text{estado inicial}] \times Q = \begin{pmatrix} 0.2 & 0.2 & 0.2 & 0.2 & 0.2 \\ \end{pmatrix} \times \begin{pmatrix} 0 & .5 & 0 & 0 & .5 \\ .5 & 0 & .5 & 0 & 0 \\ 0 & .5 & 0 & .5 & 0 \\ 0 & 0 & .5 & 0 & .5 \\ .5 & 0 & 0 & .5 & 0 \\ \end{pmatrix} = \begin{pmatrix} 0.2 & 0.2 & 0.2 & 0.2 & 0.2 \\ \end{pmatrix} \] Uma consequência dessa propriedade é que, uma vez que uma cadeia atinge sua distribuição estacionária, a distribuição estacionária continuará sendo a distribuição dos estados daí em diante.
Também podemos demonstrar a distribuição estacionária simulando uma longa cadeia a partir deste exemplo.
n = 5000
x = numeric(n)
x[1] = 1 # fixando o estado 1 para o tempo 1
for (i in 2:n) {
# amostra aleatoriamente o próximo estado (de valores inteiros de 1 a 5) com probabilidades oriundas da matriz de transição Q, baseado no valor anterior de X.
x[i] = sample.int(5, size=1, prob=Q[x[i-1],]) # 5 na função `sample.int` representa valores de 1:5 = {1,2,3,4,5}
}
table(x) / nx
1 2 3 4 5
0.2044 0.2026 0.1996 0.1960 0.1974 A distribuição geral das visitas aos estados é aproximadamente igual à distribuição estacionária.
Como acabamos de ver, se você simular uma cadeia de Markov com muitas iterações, as amostras podem ser usadas como uma amostra de Monte Carlo da distribuição estacionária. Como exemplo de aplicação no ramo da estatística é exatamente assim que as cadeias de Markov podem ser usadas em inferência bayesiana. Nesse caso para simular a partir de uma distribuição posterior complicada, configuraremos e executaremos uma cadeia de Markov cuja distribuição estacionária é a distribuição posterior.
É importante notar que a distribuição estacionária nem sempre existe para uma determinada cadeia de Markov. A cadeia de Markov deve ter certas propriedades, que não discutiremos aqui. No entanto, os algoritmos da cadeia de Markov que usaremos em lições futuras para a estimativa de Monte Carlo têm garantia de produzir distribuições estacionárias.
Exemplo: estado contínuo
O exemplo do caminho aleatório contínuo que demos anteriormente não tem uma distribuição estacionária. No entanto, podemos modificá-lo para que tenha uma distribuição estacionária.
Deixe a distribuição de transição ser \(p(X_{t+1} | X_t=x_t) = \text{N}(\phi x_t, 1)\) Onde \(-1 < \phi < 1\). Ou seja, a distribuição de probabilidade para o próximo estado é Normal com variância \(1\) e média igual a \(\phi\) vezes o estado atual. Enquanto \(\phi\) está entre \(- 1\) e \(1\), então a distribuição estacionária existirá para este modelo.
Vamos simular esta cadeia para \(\phi = - 0.6\)
n = 1500
x = numeric(n)
phi = -0.6
for (i in 2:n) {
x[i] = rnorm(1, mean=phi*x[i-1], sd=1.0)
}
plot(x, type = "l", xlab = "tempo")
A distribuição estacionária teórica para esta cadeia é normal com média \(0\) e variância \(1 / ( 1 -\phi^2)\), que em nosso exemplo é aproximadamente igual a \(1.562\). Vamos olhar um histograma de nossa cadeia e compará-lo com a distribuição estacionária
hist(x, freq=FALSE)
curve(dnorm(x, mean=0.0, sd=sqrt(1.0/(1.0-phi^2))), col="red", add=TRUE)
legend("topright", legend="Distribuição estacionária teórica", col="red", lty=1, bty="n")
Parece que a cadeia atingiu a distribuição estacionária. Portanto, poderíamos tratar esta simulação da cadeia como uma amostra de Monte Carlo da distribuição estacionária, uma normal com média \(0\) e variância \(1.562\).
Como a maioria das distribuições posteriores que veremos são contínuas, nossas simulações de Monte Carlo com cadeias de Markov serão semelhantes a este exemplo.
Este conteúdo está disponível por meio da Licença Creative Commons 4.0
