Os teoremas limites clássicos de probabilidade se referem à sequencias de variáveis aleatórias independentes e identicamente distribuídas (i.i.d.). Se \(X_1,X_2,...\) é uma sequência de variáveis aleatórias com uma média comum, \(E[X]=\mu < \infty\), e seja a v.a. \(S_n = X_1 + ... + X_n\).

A Lei dos Grandes Números informa que a sequência das médias \(S_n/n\) converge para \(\mu\), quando \(n \to \infty\).

Existem duas versões da Lei, a fraca e a forte

Lei Fraca dos Grandes Números

A Lei Fraca dos Grandes Números é um resultado em Teoria da Probabilidade também conhecido como Teorema de Bernoulli’s. De acordo com a lei, a média dos resultados obtidos por um grande número de tentativas é próximo a média da população.

Seja \(X_i ... X_n\) uma sequência de variáveis aleatórias identicamente distribuídas e independentes \(iid\), cada uma possuindo média \(\mu\) e variância \(\sigma^2\). E a variável aleatória \(\overline{X}\), definida como,

\[\overline{X}= \frac{X_{1} + \ \ldots\ + X_{n}}{n} = \frac{S_n}{n}\]

Então o valor esperado da variável aleatória \(\overline{X}\) é,

\[ E[\overline{X}]=E\left[\frac{X_{1} + \ldots + X_{n}}{n}\right]\\ E[\overline{X}]=\frac{1}{n}(E[X_1] + \ldots\ + E[X_n])\\ E[\overline{X}]= \frac{n \mu}{n}= \mu \]

E a variância é,

\[ V(\overline{X})= V\left(\frac{X_{1} + \ldots + X_{n}}{n}\right)\\ V(\overline{X})= \frac{1}{n^{2}}[V(X_{1}) + \ldots + V(X_{n})]\\ V(\overline{X})= \frac{1}{n^{2}}[\sigma^{2} + \ldots + \sigma^{2}]\\ V(\overline{X})= \frac{\sigma^{2}}{n}\\ \]

Valor Esperado e Variância

Seja \(\overline{X}\) uma variável aleatória definida como, \[ \overline{X} = \frac{S_n}{n} = \frac{X_{1} + \ldots + X_{n}}{n} \] o valor esperado e a variância são, \[ E[\overline{X}] = \mu\\ V(\overline{X})= \frac{\sigma^{2}}{n}\\ \]

Pela desigualdade de Chebyshev temos que,

\[ \lim_{n\to\infty} \mathbb{P}\left(|\frac{X_{1} + \ldots + X_{n}}{n} - \mu| \ge \epsilon\right) \le \frac{\sigma^2}{n\epsilon^2} \]

De forma simplificada significa dizer que quando \(n \to \infty\) a v.a. \(\overline{X}\) que é a média amostral será igual a média populacional \(\mu\). Ou seja a probabilidade de que a diferença entre a média amostral e a média populacional ser maior que um valor constante qualquer (\(\epsilon > 0\)), tende a zero.

Teorema - Lei Fraca dos Grandes Números
Para qualquer \(\epsilon > 0\), \[ \lim_{n\to\infty} \mathbb{P}\left(|\frac{S_n}{n} - \mu| < \epsilon\right) = 1 \]

Enquanto a lei fraca assegura que para um valor grande de \(n\), a média \(S_n/n\) ou \(\overline{X}\) é próxima de \(\mu\) com alta probabilidade, a lei não informa que, uma vez estando próxima de \(\mu\), a sequência de médias permanecerá próxima de \(\mu\).

Lei Forte dos Grandes Números

A lei forte dos grandes números assegura que com probabilidade 1 a sequência de médias \(\frac{S_1}{1}, \frac{S_2}{2}, \frac{S_3}{3}, ...\) tende a média \(\mu\) e se comporte dessa forma.

Teorema - Lei Forte dos Grandes Números
\[ \mathbb{P}\left(\lim_{n\to\infty} \frac{S_n}{n} = \mu \right) = 1 \]

Lei Grandes Números

Em resumo a lei do grandes números demonstra que,

Lei dos Grandes Números
\[ \frac{S_n}{n} - \mu \to 0 \quad \quad, n \to \infty \]

A seguir é apresentado dois exemplos dessa convergência, a partir da simulação de valores de uma população Binomial e uma Normal.

# Simulação da Lei dos Grandes Números: Distribuição Binomial utilizando o R (Rstudio)
# Parâmetros da Binomial Bi(n,p)
n = 5000
p = 0.4

# dataframe
df = data.frame(bi = rbinom(n, 1, p)  ,count = 0, proportion = 0)
df$count = cumsum(df[,1])
df$proportion = df$count/(1:n)

# plot
plot(df$proportion, type='l',
     main = "Simulação da Lei dos Grandes Números - Binomial",
     xlab="n", ylab="Proporção amostral")
abline(h = p, col="red")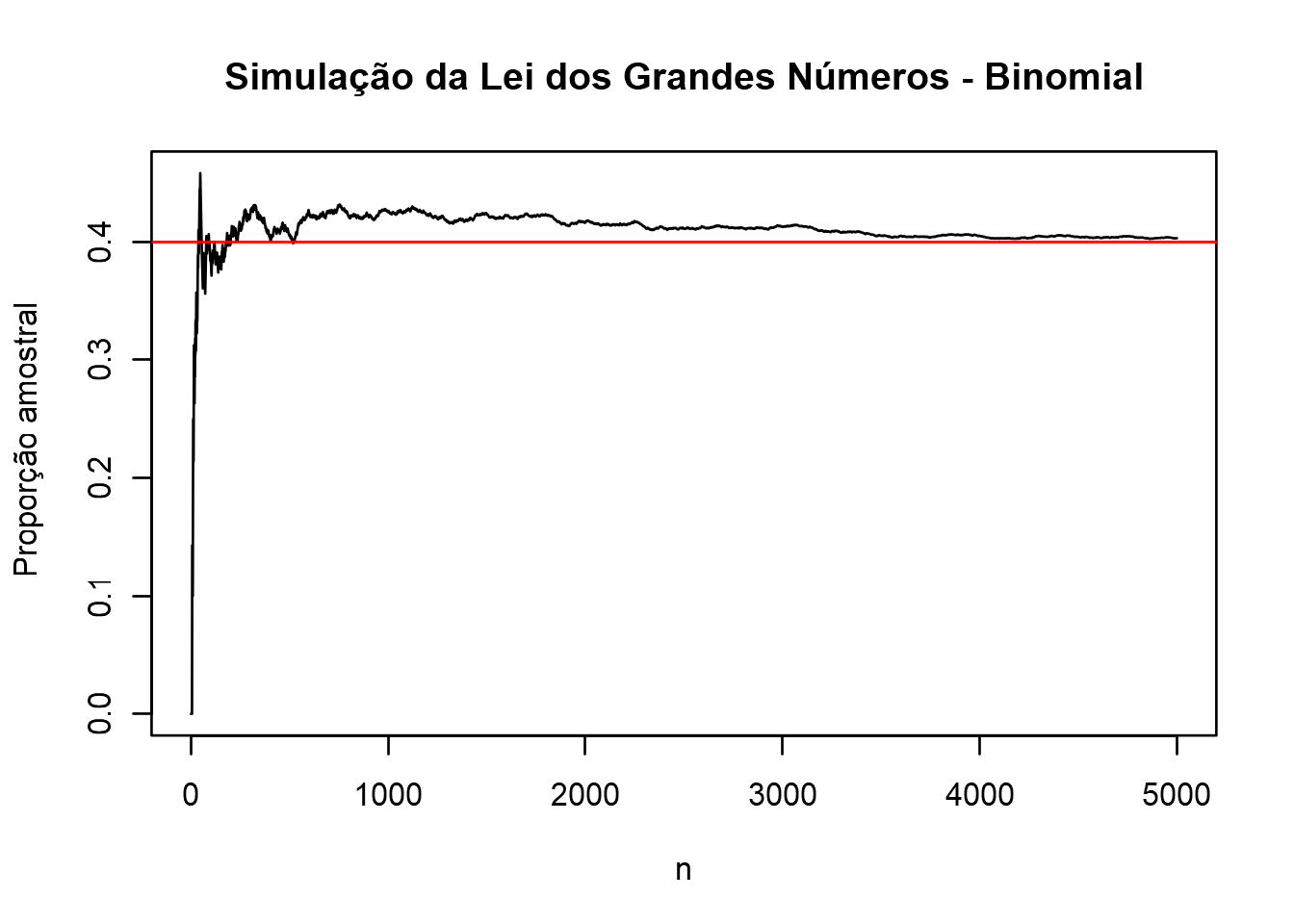

# Simulação da Lei dos Grandes Números: Distribuição Normal utilizando o R (Rstudio)
# Parâmetros da Normal N(media,desvio padrão)
n = c(1:2000)
mu = 3 # média populacional
sd = 0.5 # desvio padrão populacional
x = rnorm(2000,mu,sd) # amostras aleatórias da v.a. normal com media = mu e desvio padrão = sd
s = cumsum(x) # soma cumulativa
medias = s/n  # média pontual

plot(medias, type="l",
    main = "Simulação da Lei dos Grandes Números - Normal",
    xlab="n", ylab="Média amostral")
abline(h = 3, col="red")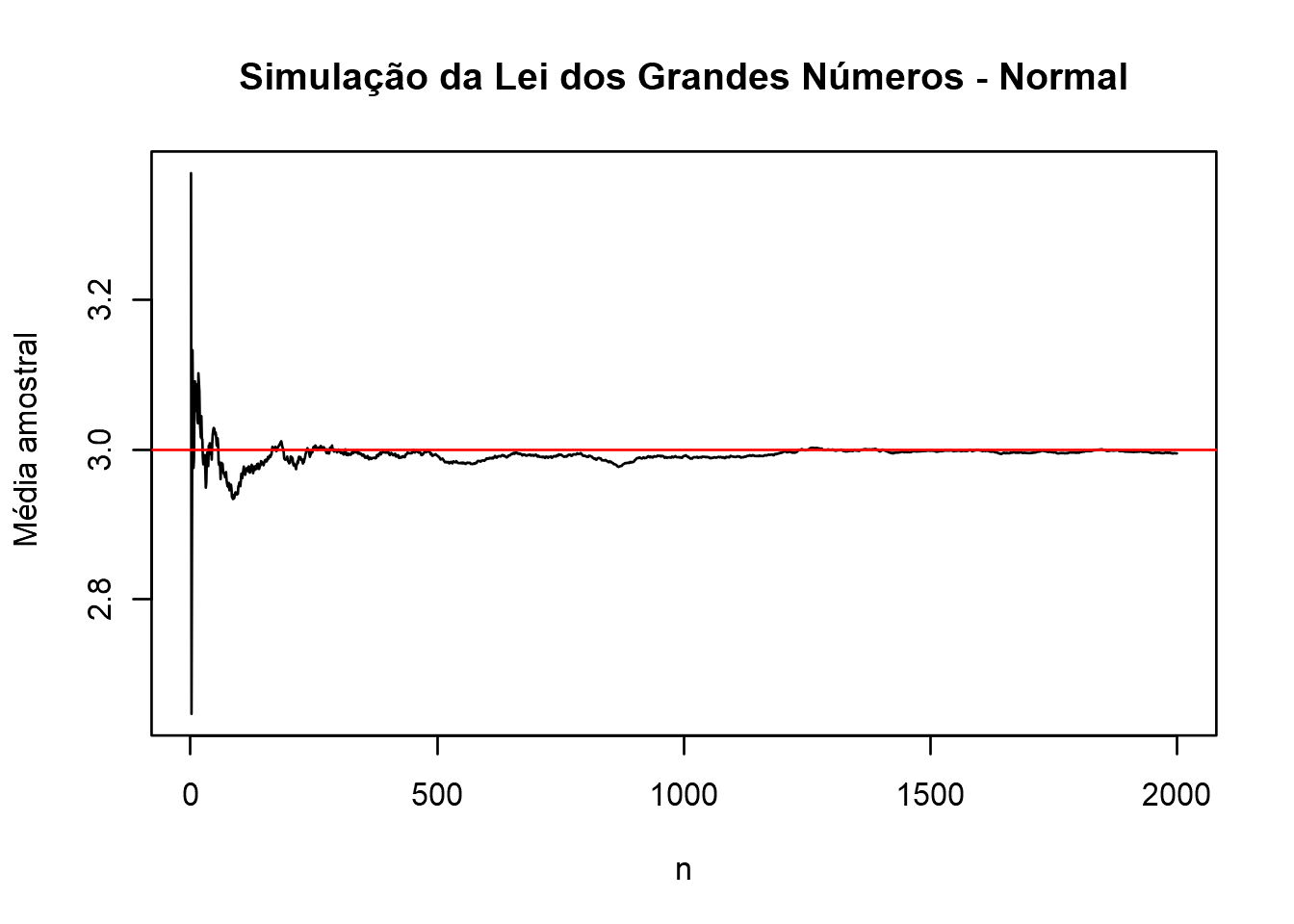

Teorema Central do Limite

O Teorema Central do Limite (TCL) é um dos teoremas mais importante dentro da Estatística e Probabilidade. É um teorema limite que foi considerado como “Central” pelo matemático húngaro George Pólya.

Brevemente, o Teorema Central do Limite estabelece que a distribuição da soma (ou média) de um grande número de variáveis aleatórias independentes e identicamente distribuídas (i.i.d.) será aproximadamente normal, independentemente da distribuição subjacente (dessas variáveis).

Esse é um dos motivos porque a distribuição normal é utilizada em tantos testes estatísticos.

Vamos abordar o teorema apresentando de forma bastante resumida alguns pontos importantes e suas consequências.

Processo de soma parcial

Suponha que \(X_1, X_2,...\) é uma sequência de variáveis aleatórias independentes e identicamente distribuídas, com uma distribuição de densidade \(f_X(x)\), média \(\mu\) e variância \(\sigma^2\) em comum. Assumimos que \(0 < \sigma^2 < \infty\), para que as variáveis aleatórias sejam realmente aleatórias e não constantes.

Seja, \[ S_n = X_1 + ...+ X_n \quad \quad, n \in \mathbb{N} \] Por convenção temos que \(S_0 = 0\), uma vez que a soma é sobre um conjunto vazio.

O processo aleatório (estocástico) \(S_0, S_1, S_2,...\) é chamado de processo de soma parcial associado com \(X\).

Em termos estatísticos (para diferenciar da teoria de probabilidade), a sequência \(X_1, X_2, ...\) corresponde ao processo de amostragem de uma dada população (ou distribuição). De forma particular, \((X_1, X_2, ...,X_n)\) é uma amostra aleatória de tamanho \(n\) dessa distribuição, e a correspondente média amostral é \[\overline{X}= \frac{S_n}{n} = \frac{X_{1} + \ \ldots\ + X_{n}}{n} = \frac{1}{n}\sum_{i=1}^{n}X_i\]

E pela Lei dos Grandes Números, \(S_n \to \mu\) quando \(n \to \infty\) com probabilidade 1.

Note que, se \(n \in \mathbb{N}\), então pela propriedade da linearidade do valor esperado, para v.a. independentes: \[ E[S_n] = n\mu\\ V(S_n) = n\sigma^2\\ \]

Como pode-se notar acima não podemos esperar que \(S_n\) tenha uma distribuição limitante quando \(n \to \infty\), pois a \(V(S_n) \to \infty\) bem como o \(E[S_n] \to \infty\).

Porém antes mesmo de estabelecer esses limites podemos verificar a forma da distribuição a medida que \(n\) aumenta, e visualizar a pressuposição e deduções dos teoremas e leis apresentadas até aqui.

Através de uma simulação Monte Carlo verificaremos a forma de uma distribuição da variável aleatória \(S_n\), que é a soma de v.a.s independentes e identicamente distribuídas.

Começaremos a simulação da soma de duas v.a. uniformes \(X \sim U(0,1)\)

\[ S_n = X_1 + ...+ X_n\\ \\ S_2 = X_1 + X_2\\ \]

par(mfrow=c(2,2))
u1=runif(1000000)
hist(u1, freq=FALSE, breaks=100, col="lightblue", main="U1",ylab="Densidade")
u2=runif(1000000)
hist(u2, freq=FALSE, breaks=100, col="green", main="U2",ylab="Densidade")

S2=u1+u2
hist(S2, freq=FALSE, breaks=100, col="blue", ylab="Densidade",
     main=expression(paste("Distribuição de ",S[2],"=",U[1]+U[2])))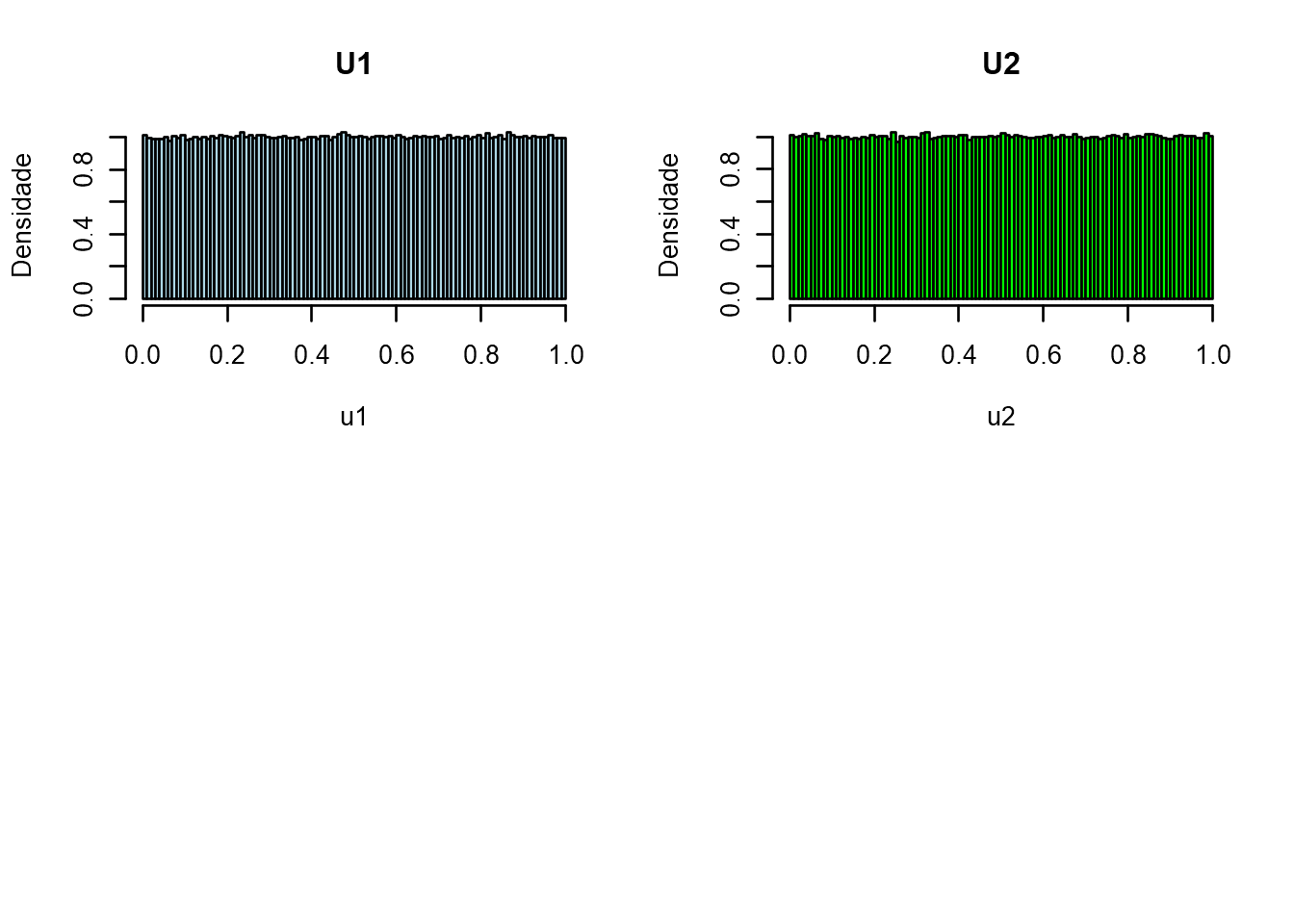

\[ S_n = X_1 + ...+ X_n\\ \\ S_2 = X_1 + X_2 + X_3\\ \]

par(mfrow=c(2,2))
u1=runif(1000000)
hist(u1, freq=FALSE, breaks=100, col="lightblue", main="U1",ylab="Densidade")
u2=runif(1000000)
hist(u2, freq=FALSE, breaks=100, col="green", main="U2",ylab="Densidade")
u3=runif(1000000)
hist(u3, freq=FALSE, breaks=100, col="gray", main="U3",ylab="Densidade")

S3=u1+u2+u3
hist(S3, freq=FALSE, breaks=100, col="blue", ylab="Densidade",
     main=expression(paste("Distribuição de ",S[3],"=",U[1]+U[2]+U[3])))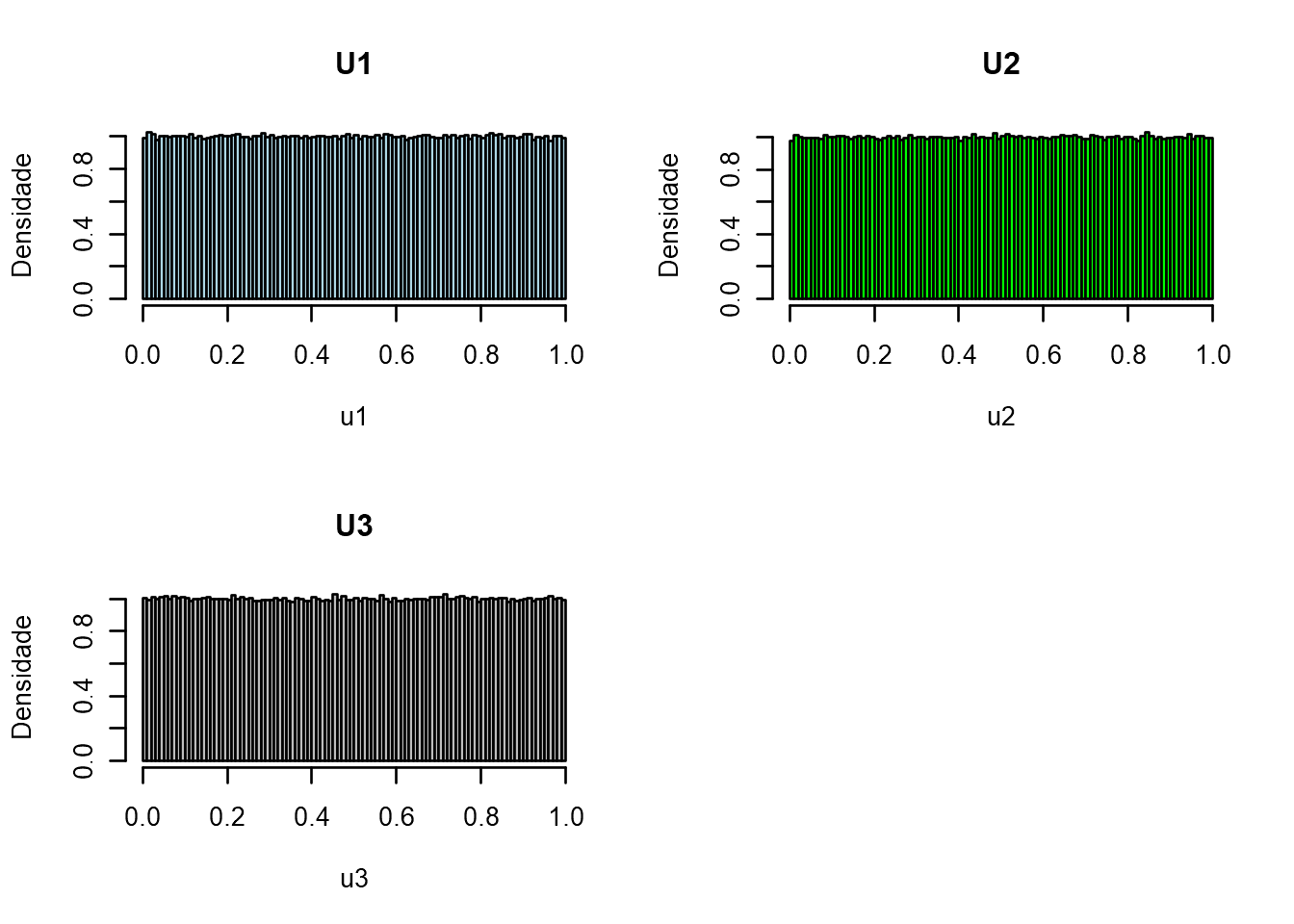

\[ S_n = X_1 + ...+ X_n\\ \\ S_6 = X_1 + X_2 + X_3 + X_4 + X_5 + X_6\\ \]

u1=runif(1000000)
u2=runif(1000000)
u3=runif(1000000)
u4=runif(1000000)
u5=runif(1000000)
u6=runif(1000000)
S6=u1+u2+u3+u4+u5+u6 # soma de v.a.s uniformes U(0,1)


layout(matrix(c(1,2,3,1,2,3,4,5,6,4,5,6,7,7,7,7,7,7), nrow = 6, ncol = 3, byrow = TRUE))
hist(u1, freq=FALSE, breaks=100, col="gray", main="U1",ylab="Densidade") #1
hist(u2, freq=FALSE, breaks=100, col="gray", main="U2",ylab="Densidade") #2
hist(u3, freq=FALSE, breaks=100, col="gray", main="U3",ylab="Densidade") #3
hist(u4, freq=FALSE, breaks=100, col="gray", main="U4",ylab="Densidade") #4
hist(u5, freq=FALSE, breaks=100, col="gray", main="U5",ylab="Densidade") #5
hist(u6, freq=FALSE, breaks=100, col="gray", main="U6",ylab="Densidade") #6
hist(S6, freq=FALSE, breaks=100, col="blue", ylab="Densidade",
     main=expression(paste("Distribuição de ",S[6],"=",U[1],"+...+",U[6]))) #7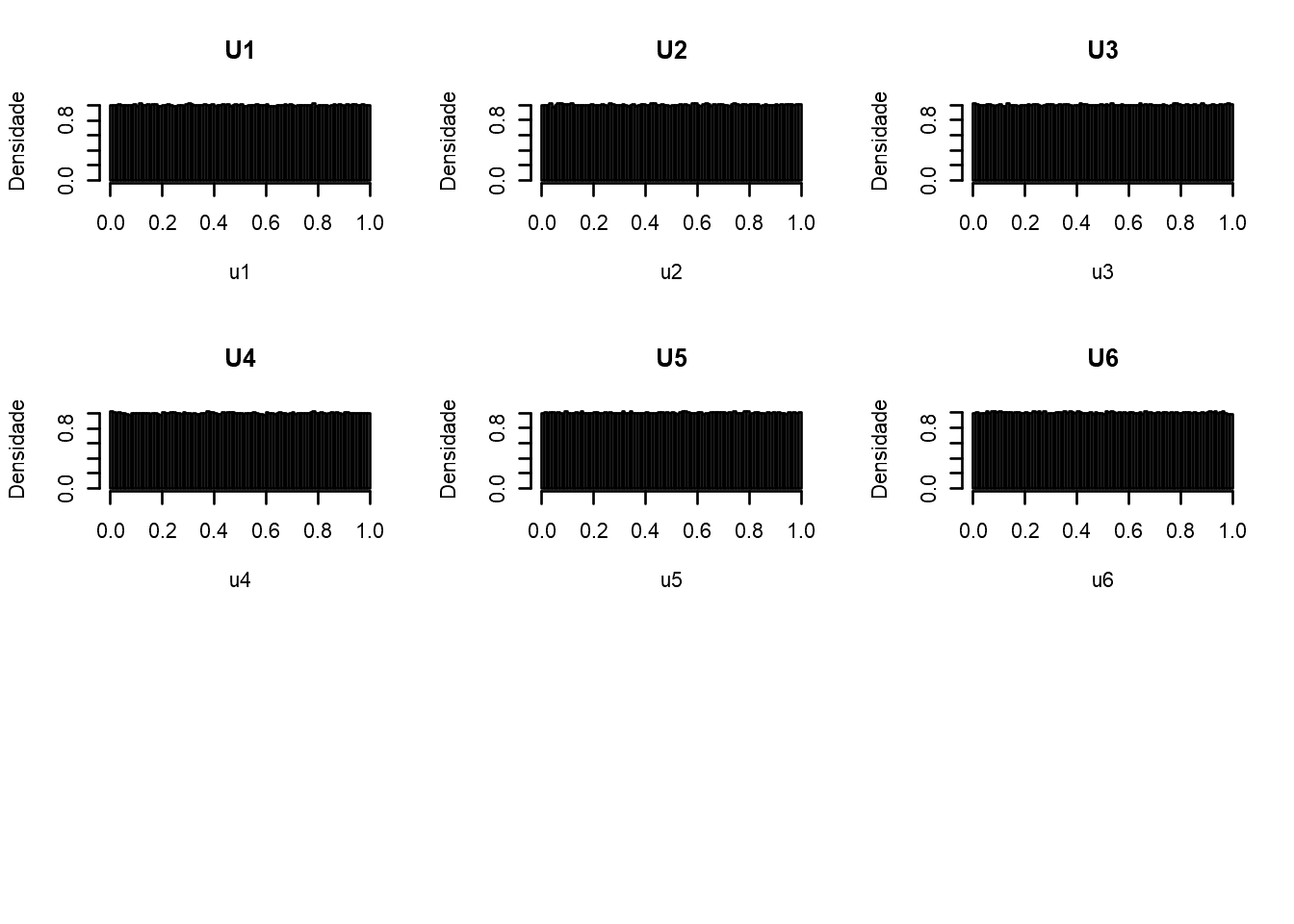

Nota-se que a forma da distribuição \(S_n\) converge em uma distribuição normal com \(E[S_n] = n\mu\) e \(V(S_n)=n\sigma^2\).

Porém note que a distribuição irá se degenerar quando \(n \to \infty\), pois

  • quando \(E[S_n] \to \infty\) e \(V(S_n)\to \infty\).
  • De forma similar para \(S_n/n = \overline{X}\), \(E[\overline{X}] \to \mu\) e \(V(\overline{X})\to \sigma^2/n \to 0\).

Assim sabemos que \(S_n/n \to \mu\) quando \(n \to \infty\) com probabilidade 1, e a distribuição limite da soma de variáveis aleatórias \(S_n\) ou da média amostral \(S_n/n = \overline{X}\) irá se degenerar.

Então para se obter uma distribuição limitante de \(S_n\) ou \(S_n/n = \overline{X}\) que não se degenere, precisaremos considerar, não as variáveis aleatórias por si, mas as variáveis normalizadas,

\[ Z_n = \frac{S_n - n\mu}{\sqrt{n}\sigma} = \frac{\overline{X} - \mu}{\sigma/\sqrt{n}} \]
Teorema Central do Limite
Seja \(Z_n\) uma variável aleatória definida como, \[ Z_n = \frac{\overline{X} - \mu}{\sigma/\sqrt{n}} \sim \quad N(0,1) \] o valor esperado e a variância são, \[ E[\overline{X}] = 0\\ V(\overline{X}) = 1\\ \] O Teorema Central do Limite estabelece que a distribuição de \(Z_n\) converge em distribuição para um distribuição normal padrão quando \(n \to \infty\)

Note que o teorema não restringe a sua dedução à algum tipo específico de distribuição de \(X\). Dessa forma o teorema é válido para qualquer tipo de distribuição.

Abaixo segue o código que demonstra os resultados do teorema do limite central para a distribuição da média amostral e variância amostral de amostras obtidas de diferentes v.a.s, para as distribuições, Exponencial, Normal, Uniforme, Poisson, etc… O código foi disponibilizado por Nicole Radziwill

# Função de simulação
sdm.sim <- function(n,src.dist=NULL,param1=NULL,param2=NULL) {
   r <- 10000  # Number of replications/samples - DO NOT ADJUST
   
   # This produces a matrix of observations with  
   # n columns and r rows. Each row is one sample:
   my.samples <- switch(src.dist,
    "E" = matrix(rexp(n*r,param1),r),
    "N" = matrix(rnorm(n*r,param1,param2),r),
    "U" = matrix(runif(n*r,param1,param2),r),
    "P" = matrix(rpois(n*r,param1),r),
    "C" = matrix(rcauchy(n*r,param1,param2),r),
        "B" = matrix(rbinom(n*r,param1,param2),r),
    "G" = matrix(rgamma(n*r,param1,param2),r),
    "X" = matrix(rchisq(n*r,param1),r),
    "T" = matrix(rt(n*r,param1),r))
   all.sample.sums  <- apply(my.samples,1,sum)
   all.sample.means <- apply(my.samples,1,mean)   
   all.sample.vars  <- apply(my.samples,1,var) 
   par(mfrow=c(2,2))
   hist(my.samples[1,],col="gray",
        main="Distribuição de uma amostra",
        ylab="Frequência")
   hist(all.sample.sums,col="gray",
        main="Distribuição amostral da soma",
        ylab="Frequência")
   hist(all.sample.means,col="gray",
        main="Distribuição amostral da média",
        ylab="Frequência")
   hist(all.sample.vars,col="gray",
        main="Distribuição amostral da variância",
        ylab="Frequência")
}

Simulações

Simulação da Distribuição amostral (\(n=50\)) de uma população (Exponencial, \(\lambda = 1\)), um total de 10000 amostras.

sdm.sim(50,src.dist="E",param1 = 1) # Exemplo para distribuição Exponencial "E"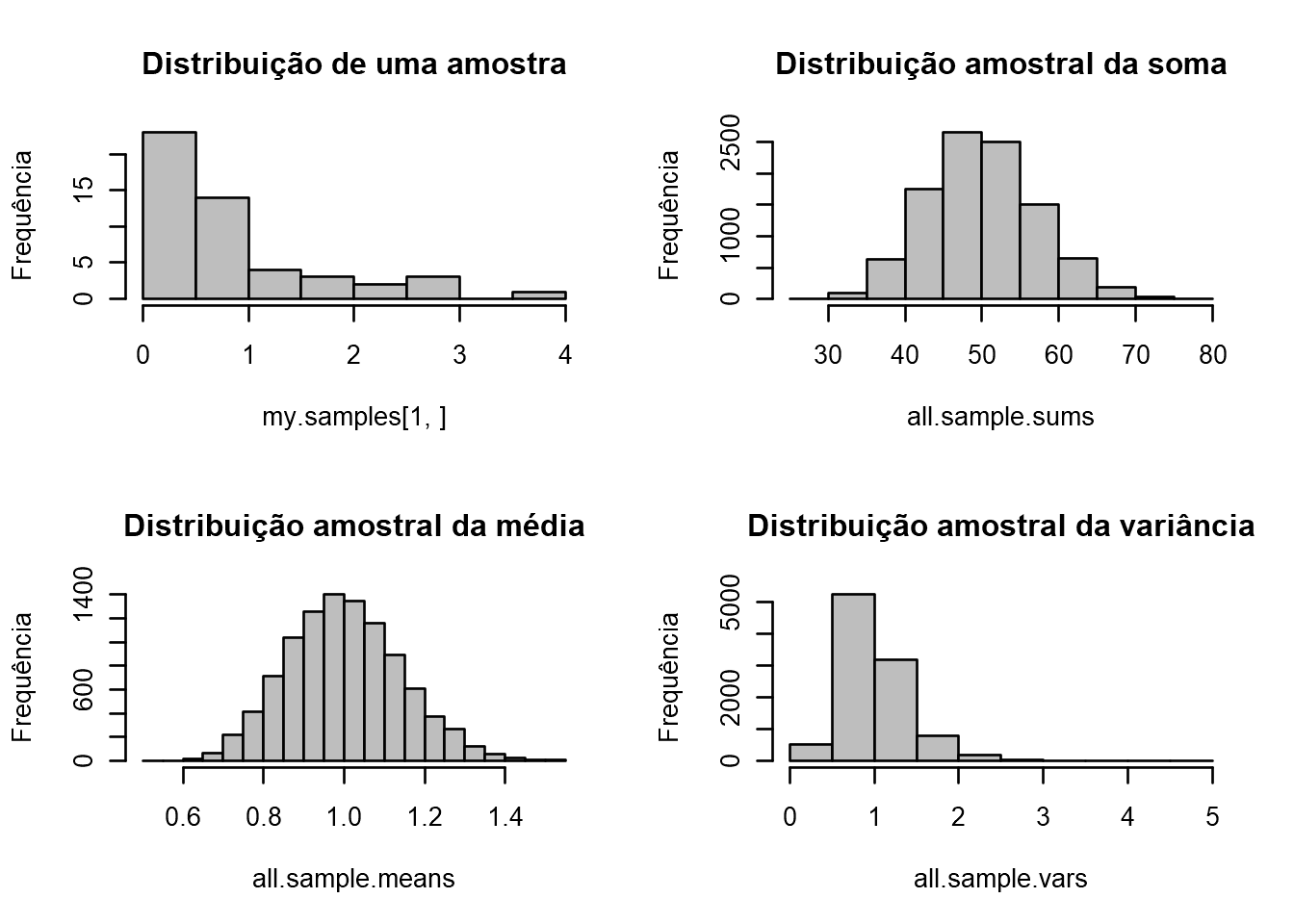

Simulação da Distribuição amostral (\(n=50\)) de uma população (Normal, \(\mu = 180, \sigma = 3\)), um total de 10000 amostras.

sdm.sim(50,src.dist="N",param1 = 180, param2 = 3) # Exemplo para distribuição Exponencial "E"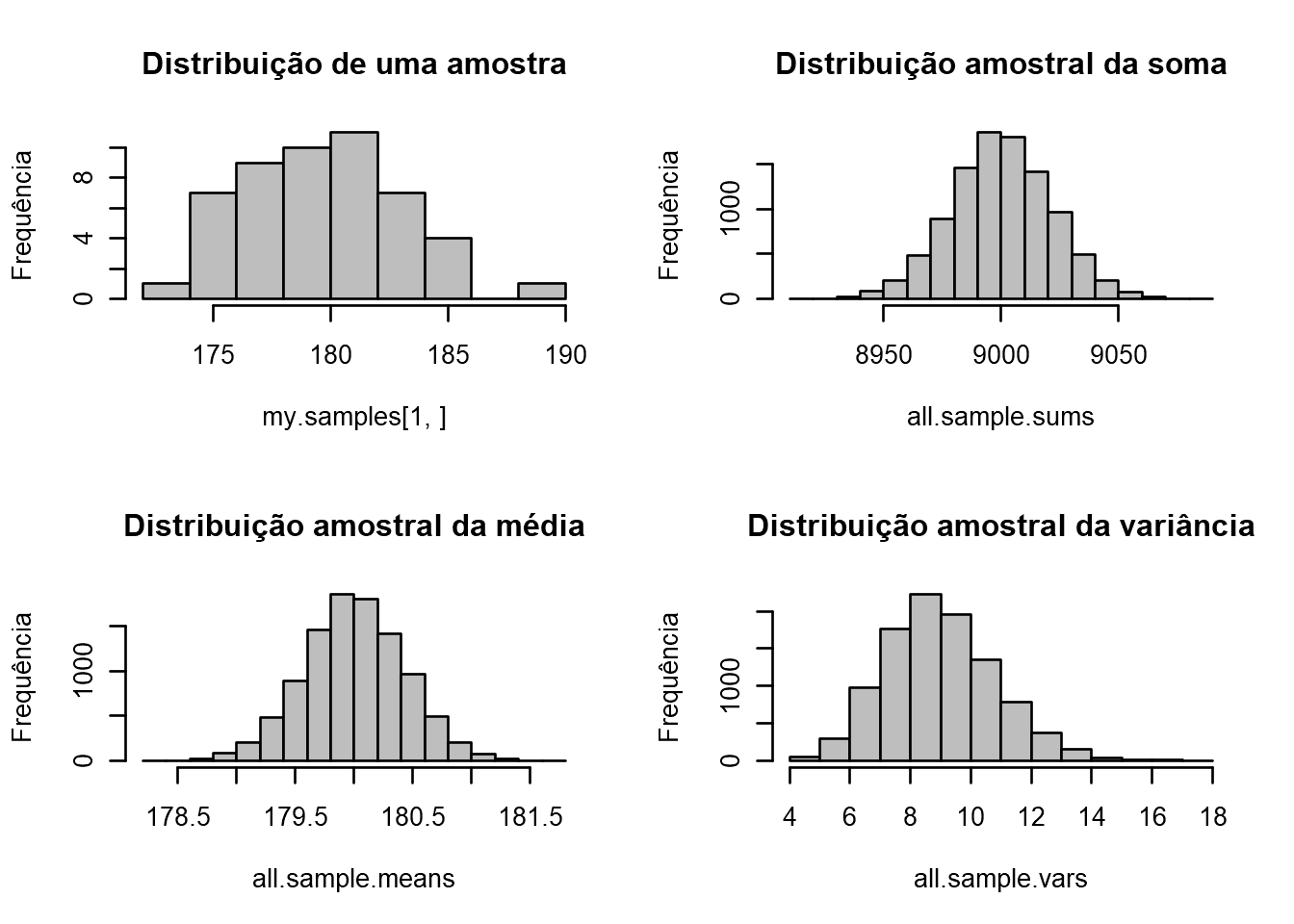

Simulação da Distribuição amostral (\(n=50\)) de uma população (Uniforme, \(a = 4, b = 12\)), um total de 10000 amostras.

sdm.sim(50,src.dist="U",param1=4, param2 = 12) # Exemplo para distribuição Exponencial "E"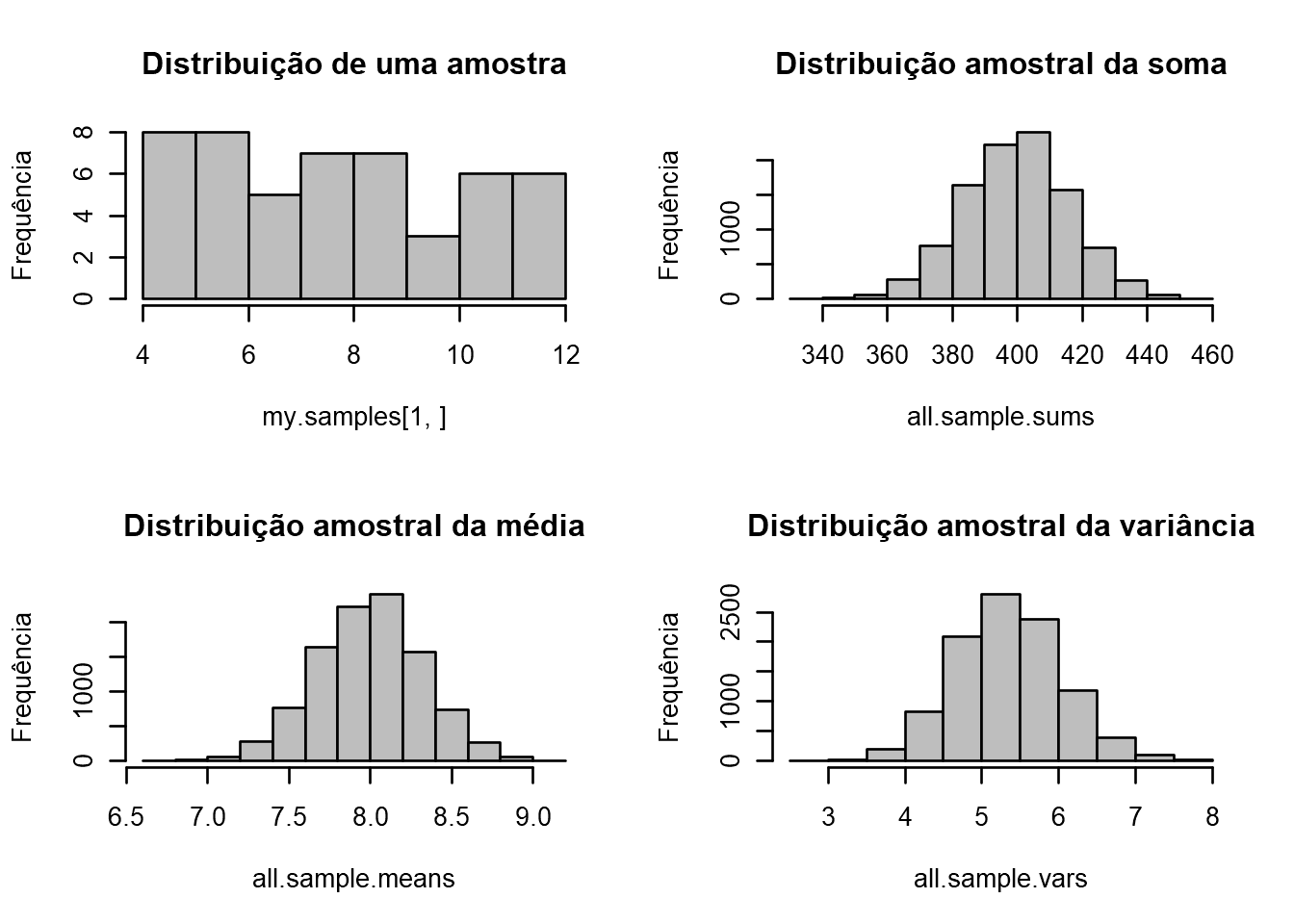

Licença Creative Commons 4.0

Este conteúdo está disponível por meio da Licença Creative Commons 4.0