As distribuições do tempo de espera é outra importante classe de problemas associados com a quantidade de tempo que leva para a ocorrência de um evento específico de interesse. Dentro dessa classe de problemas se enquadram duas distribuições bastante conhecidas, são elas:

Distribuição Binomial Negativa

Podemos generalizar um problema e considerar o caso em que nós esperamos por mais de um único sucesso. Suponha que desejamos conduzir repetidos experimentos Bernoulli, observando os respectivos sucessos e falhas. Seja \(X\) a contagem do número de falhas antes de \(r\) sucessos. e \(P(Sucesso)=p\) então \(X\) possui a seguinte PMF,

Variável Aleatória Generalizada
Seja \(X\) a contagem do número de falhas antes de \(r\) sucessos.
Função Massa de Probabilidade
\[ p_X(x) = \mathbb{P}(X=x)=\left(\begin{array}{c}{r+x-1}\\{r-1}\end{array}\right) p^r(1-p)^{x} \]

Outra generalização da binomial negativa segue a mesma ideia da distribuição geométrica quanto à generalização da variável aleatória.

Variável Aleatória Generalizada
Seja \(Y\) a contagem do número de tentativas até que \(r\) sucessos ocorram.
Função Massa de Probabilidade
\[ p_Y(y) = \mathbb{P}(Y=y)=\left(\begin{array}{c}{y-1}\\{r-1}\end{array}\right) p^r(1-p)^{y-r} \]

Podemos dizer que \(X\) possui uma distribuição binomial negativa e escrever \(X \sim BinNeg(r,p)\)

Valor Esperado e variância
\[ E[X] = \frac{r}{p} \] \[ V(X) = \frac{r(1-p)}{p^2} \]
Pressupostos

  • o resultado é completamente determinado por chance (aleatório);

  • existem somente dois possíveis resultados, experimento Bernoulli;

  • todas as tentativas possuem a mesma probabilidade para um resultado em particular. Ou seja, as tentativas ou realizações do experimento são independentes;

  • isso implica que, existe uma probabilidade \(p\) de sucesso constante em cada tentativa

Exemplo - Binomial Negativa 1

Lançamos repetidas vezes uma moeda. Seja \(X\) o número de caras até que consigamos sete coroas. Qual é a probabilidade de que o número de caras seja igual a cinco até que consigamos as sete coroas,\(\mathbb{P}(X = 5)\)?

Solução

Sabemos que \(X \sim BinNeg(7,0.5)\)

Seja \(X\) o número de caras até que consigamos sete coroas, com \(p=0.5\).

Assim, temos que,

\[ \mathbb{P}(X = 5) = \left(\begin{array}{c}{7+5-1}\\{7-1}\end{array}\right) 0.5^7(1-0.5)^{5}=0.112793 \] Note que no R na função dnbinom(x,r,p) \(x\) representa o número de fracassos e \(r\) o número de sucessos.

x = 5 # fracassos
r = 7 # sucessos
p = 0.5
p_x = dnbinom(x,r,p)
p_x
[1] 0.112793

Aqui podemos ainda explicitar outras probabilidades em relação à esse experimento como por exemplo as probabilidades de que o número de fracassos varie de 1 a 15, até que 7 sucessos sejam obtidos.

x = seq(1,15,1) # fracassos
r = 7 # sucessos
p = 0.5
p_x = dnbinom(x,r,p)
plot(x,p_x,type='h',xlab='Números de fracassos até a obtenção de 7 sucessos',ylab=expression(p[X](x)))
points(x,p_x,col=2)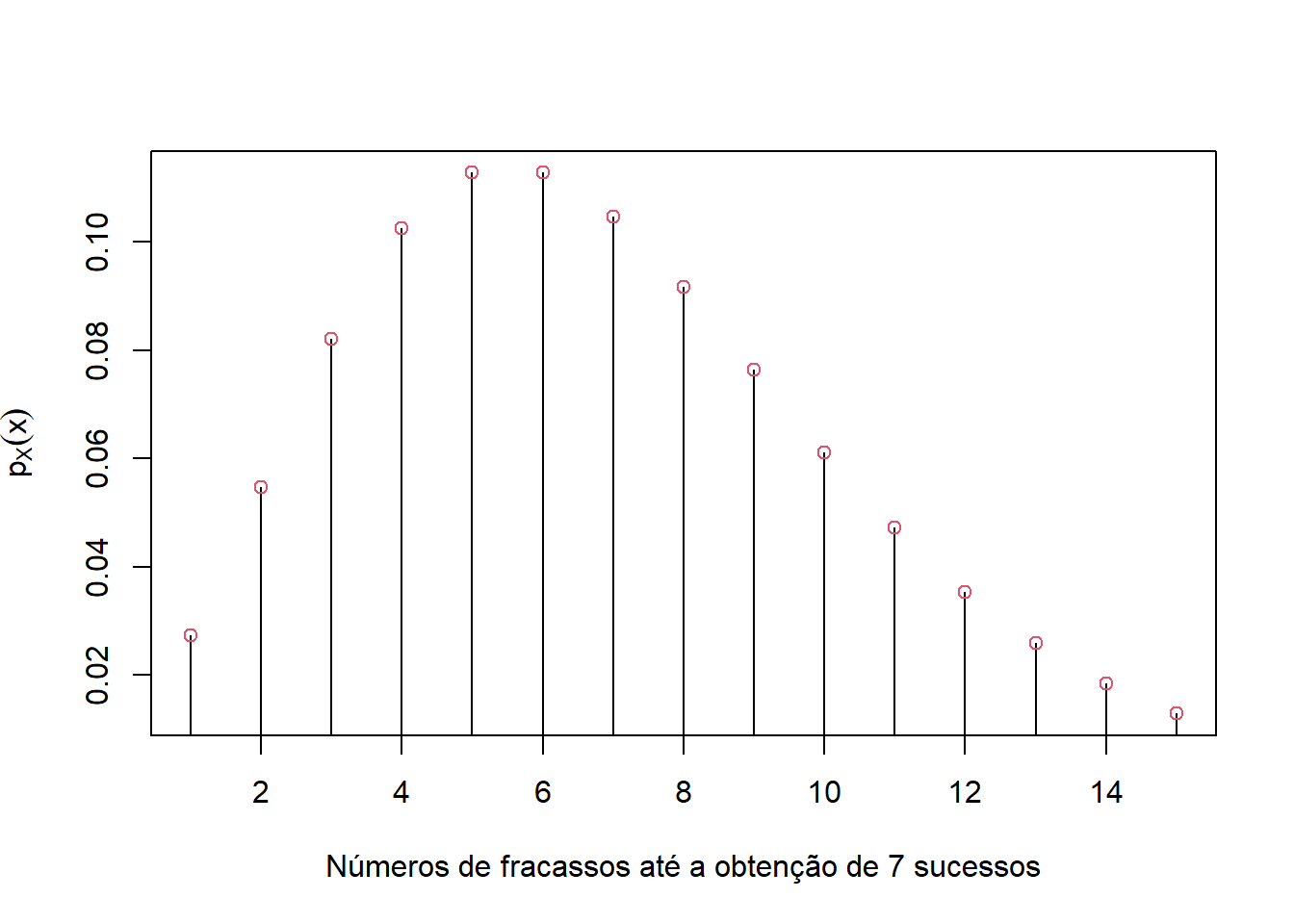

***

Exemplo - Binomial Negativa 2

considere o tempo para recarregar o flash de uma câmera de celular. Assuma que a probabilidade de que uma câmera instalada no celular durante sua montagem passe no teste é de 0.80, e que cada câmera tem seu desempenho independente. Determine as seguintes probabilidades.

  1. Qual é a probabilidade de que a segunda falha ocorra na décima câmera testada?
  2. Qual é a probabilidade de que a segunda falha ocorra no teste de quatro ou menos câmeras?
  3. Qual é o valor esperado do número de câmeras testadas para obter a terceira falha ***

Solução

  1. Qual é a probabilidade de que a segunda falha ocorra na décima câmera testada? Note que \(Y\) é igual ao número de câmeras testadas para detectar duas falhas, \(X \in \{2,3,4,...\}\). Assim \(X\) tem distribuição binomial negativa com probabilidade de falha de \(p = 1-0.8 = 0.2\) e \(r = 2\).

\[ \mathbb{P}(X = 10) = \left(\begin{array}{c}{10-1}\\{2-1}\end{array}\right) 0.2^2(1-0.2)^{10-2}=0.06039798 \] Note que no R na função dnbinom(x,r,p) \(x\) representa o número de fracassos e \(r\) o número de sucessos.

r = 2 # sucessos
x = 10-2 # fracassos
p = 0.2
p_x = dnbinom(x,r,p)
p_x
[1] 0.06039798
  1. Qual é a probabilidade de que a segunda falha ocorra no teste de quatro ou menos câmeras? Note que \(Y\) é igual ao número de câmeras testadas para detectar três falhas, \(X \in \{2,3,4,...\}\). Assim \(X\) tem distribuição binomial negativa com probabilidade de falha de \(p = 1-0.8 = 0.2\) e \(r = 2\)

\[ \mathbb{P}(X \le 4 ) = \mathbb{P}(X = 2 ) + \mathbb{P}(X = 3 ) + \mathbb{P}(X = 4 ) = 0.1808 \] Note que no R na função dnbinom(x,r,p) \(x\) representa o número de fracassos e \(r\) o número de sucessos.

r = 2 # sucessos
x = seq(2,4,1) - 2 # fracassos
p = 0.2
p_x = dnbinom(x,r,p)
p_x
[1] 0.0400 0.0640 0.0768
sum(p_x)
[1] 0.1808
  1. Qual é o valor esperado do número de câmeras testadas para obter a terceira falha

\[ E[Y]=\frac{r}{p}=\frac{3}{0.2}=15 \]

A distribuição para o item (a) e (b) é:

r = 2 # sucessos = camera com falha
x = seq(2,60,1)-2 # fracassos
p = 0.2
p_x = dnbinom(x,r,p)
plot(x,p_x,type='h',xlab='Números fracassos até a obtenção de 2 câmeras com falha',ylab=expression(p[X](x)))
points(x,p_x,col=2)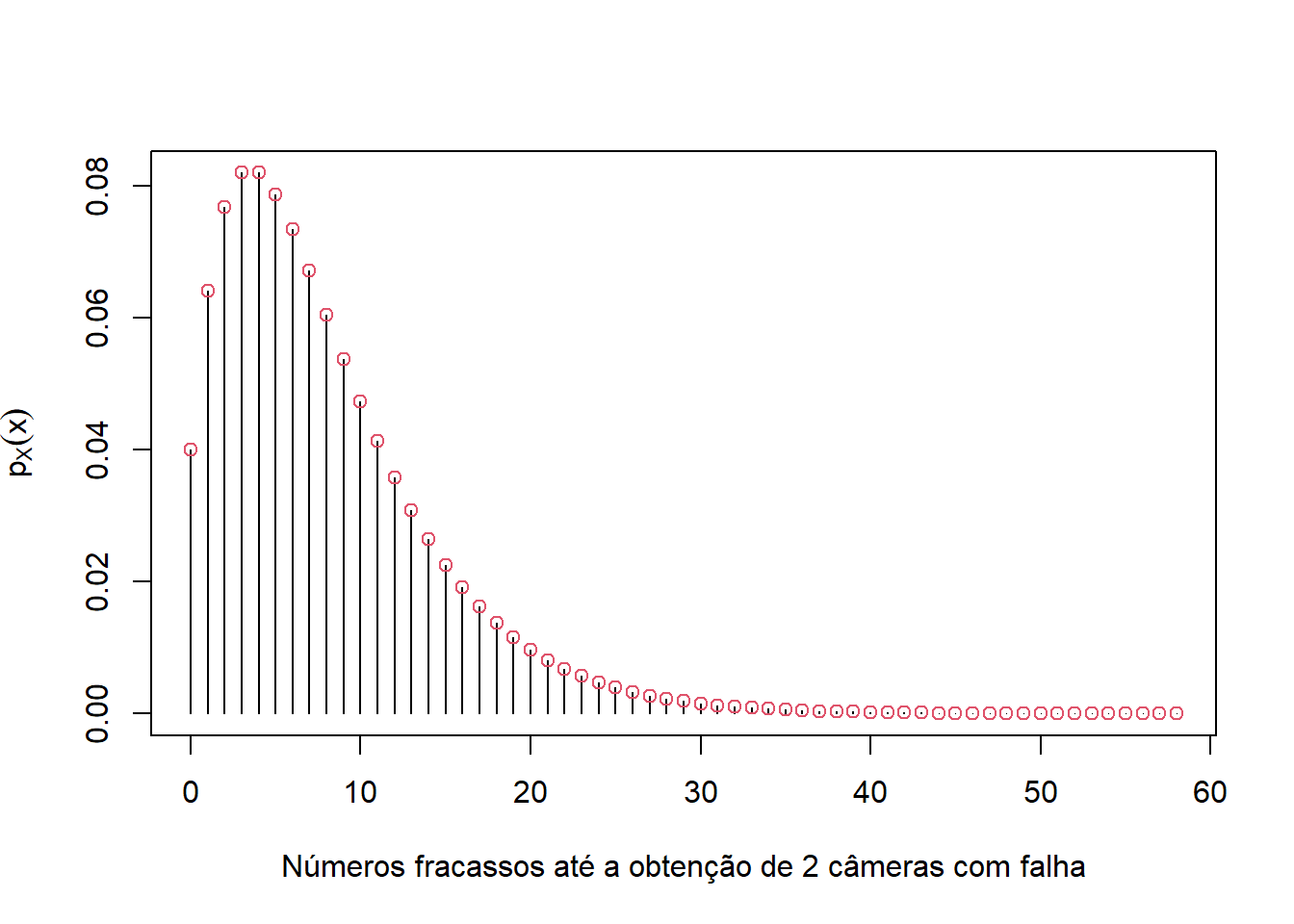

A distribuição para o item (c) é:

r = 3 # sucessos = camera com falha
x = seq(3,60,1)-3 # fracassos
p = 0.2
p_x = dnbinom(x,r,p)
plot(x,p_x,type='h',xlab='Números de fracassos até a obtenção de 2 câmeras com falha',ylab=expression(p[X](x)))
points(x,p_x,col=2)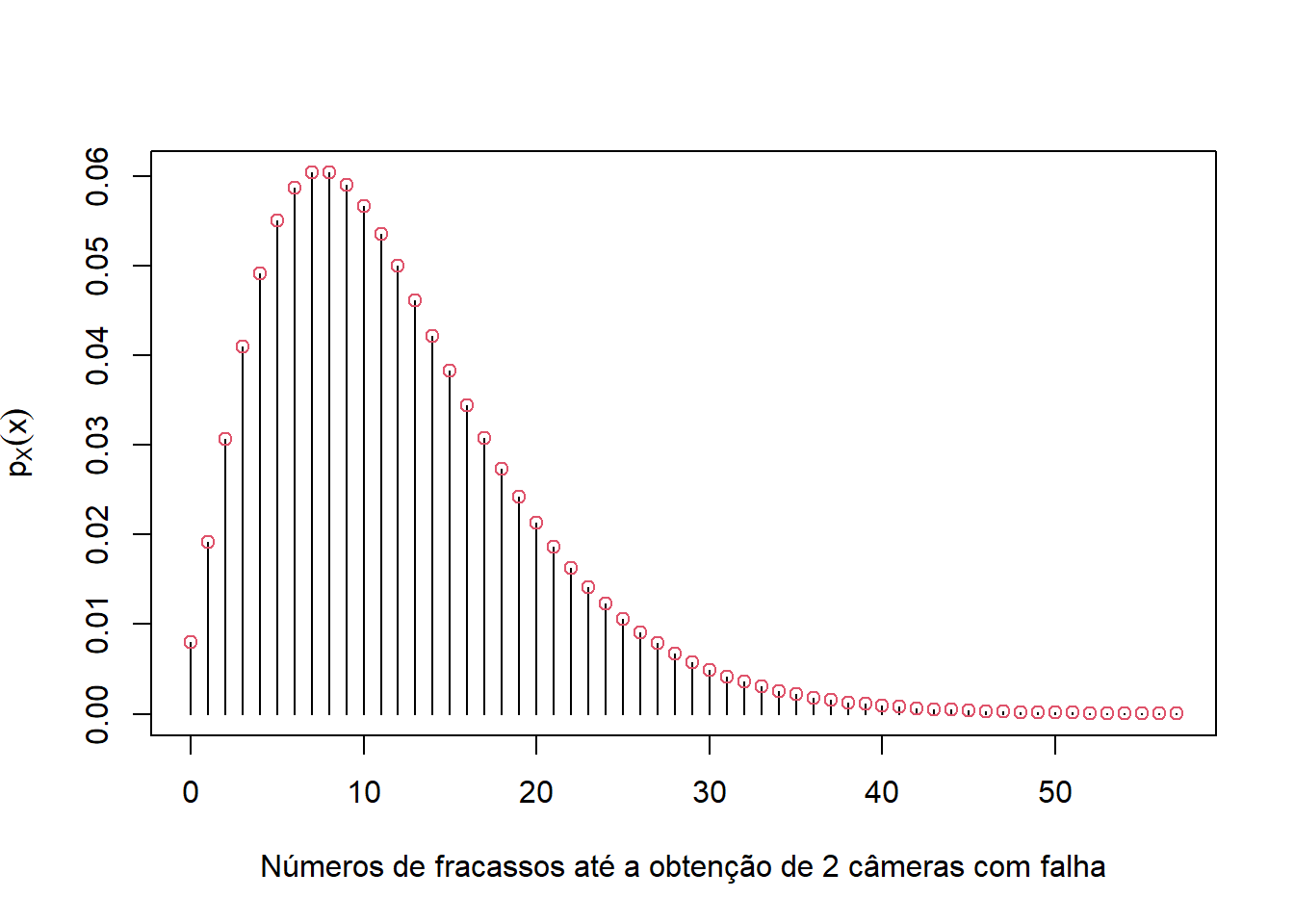

Exemplos de distribuição binomial Negativa (r,p)

r = 5 # sucessos = camera com falha
x = seq(5,120,1) - 5 # fracassos
p = 0.4
p_x = dnbinom(x,r,p)
plot(x,p_x,type='h',xlab='Exemplo de Binomial negativa com  r = 5 e p = 0.4 ',ylab=expression(p[X](x)))
points(x,p_x,col=2)

r = 5 # sucessos = camera com falha
x = seq(r,120,1) - r # fracassos
p = 0.1
p_x = dnbinom(x,r,p)
plot(x,p_x,type='h',xlab='Exemplo de Binomial negativa com  r = 5 e p = 0.1',ylab=expression(p[X](x)))
points(x,p_x,col=2)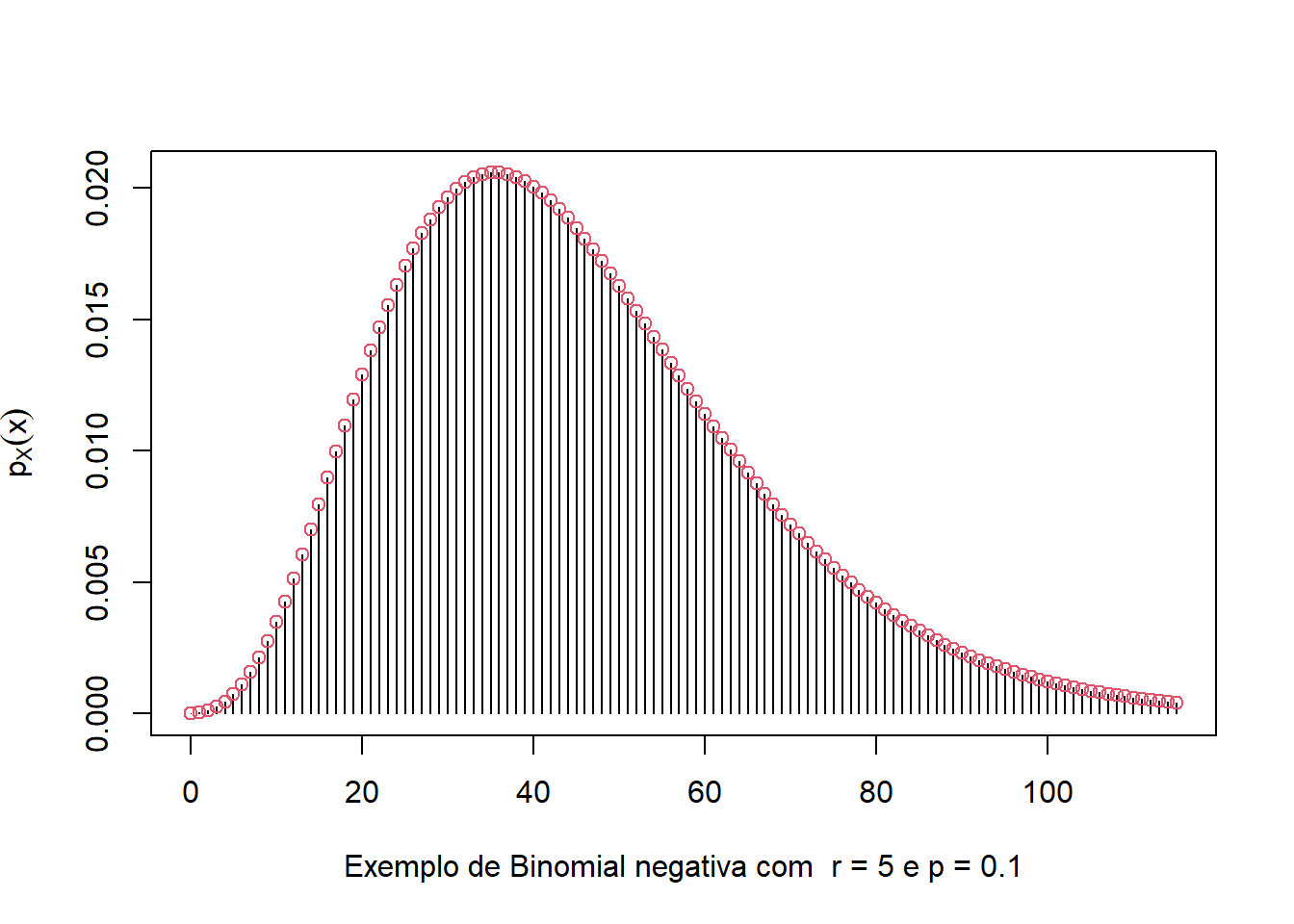

r = 10 # sucessos = camera com falha
x = seq(r,120,1) - r # fracassos
p = 0.4
p_x = dnbinom(x,r,p)
plot(x,p_x,type='h',xlab='Exemplo de Binomial negativa com  r = 10 e p = 0.4',ylab=expression(p[X](x)))
points(x,p_x,col=2)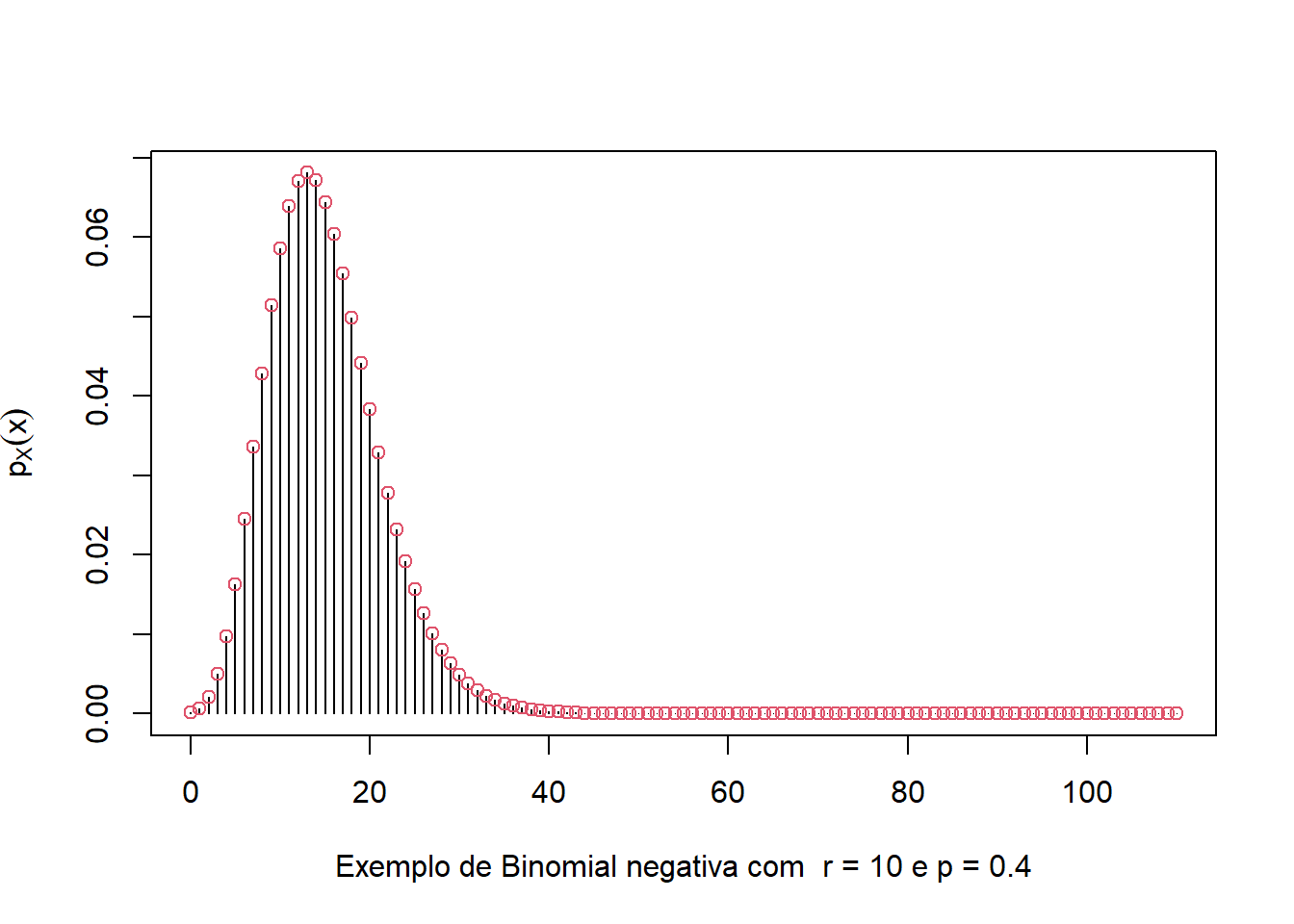

r = 3 # sucessos = camera com falha
x = seq(r,10000,1) - r # fracassos
p = 0.0005
p_x = dnbinom(x,r,p)
plot(x,p_x,type='h',xlab='Exemplo de Binomial negativa com  r = 3 e p = 0.0005',ylab=expression(p[X](x)))
points(x,p_x,col=2)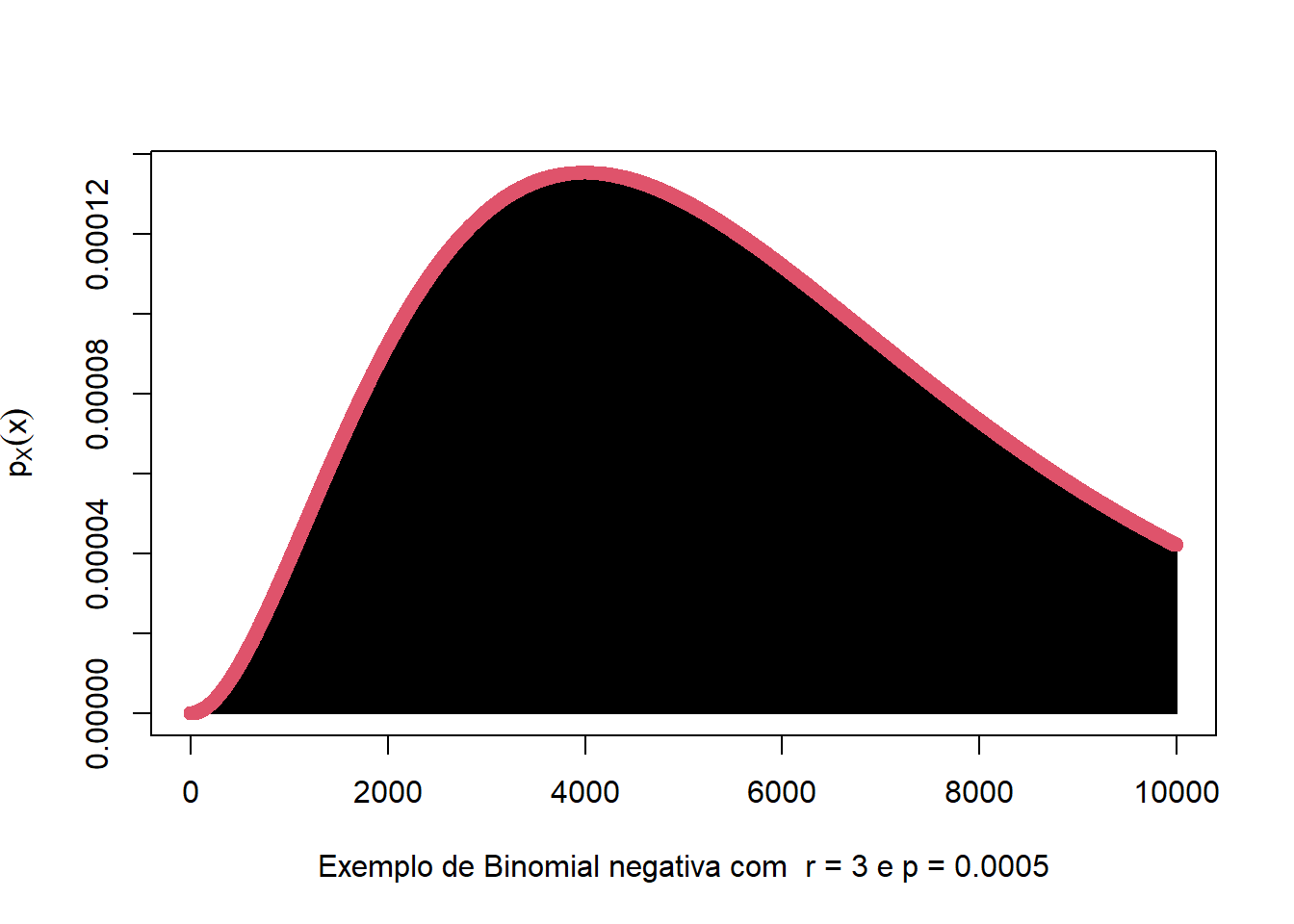

Licença Creative Commons 4.0

Este conteúdo está disponível por meio da Licença Creative Commons 4.0