Estimação de Parâmetros
Neste tópico iremos discutir dois ramos do procedimento de estimação de parâmetros: estimação pontual e estimação intervalar. Em primeiro lugar aboraderemos brevemente a estimativa pontual e o resto do tópico será focado em estimação intervalar.
Podemos encontrar um estimador fazendo uso de alguns métodos (métodos dos momentos, MM, método da máxima verossimilhança, MVS, entre outros). Para isso é necessário assumir algumas suposições sobre a distribuição da população subjacente e usar o que sabemos sobre distribuições amostrais, tanto para estudar como o estimador se comporta, bem como para encontrar intervalos de confiança para os parâmetros associados com a distribuição da população. Uma vez que temos intervalos de confiança podemos efetuar o processo de inferência e efetuar o teste de hipóteses, que é o tópico seguinte.
Este tópico será ampliado para que se saiba:
- como olhar para um problema, identificar um modelo razoável, e estimar um parâmetro associado com o modelo;
- o entendimento sobre a máxima verossimilhança;
- as propriedades dos estimadores, como bias, variância mínima, MSE;
- a diferença entre estimativa pontual vs estimativa de intervalar, e como encontrar e interpretar intervalos de confiança;
- o conceito de margem de erro e sua relação com o tamanho da amostra;
A partir do processo de estimação de parâmetros podemos realizar a inferência dos parâmetros na população subjacente a partir de uma amostra de tamanho \(n\).
Observe a figura abaixo.
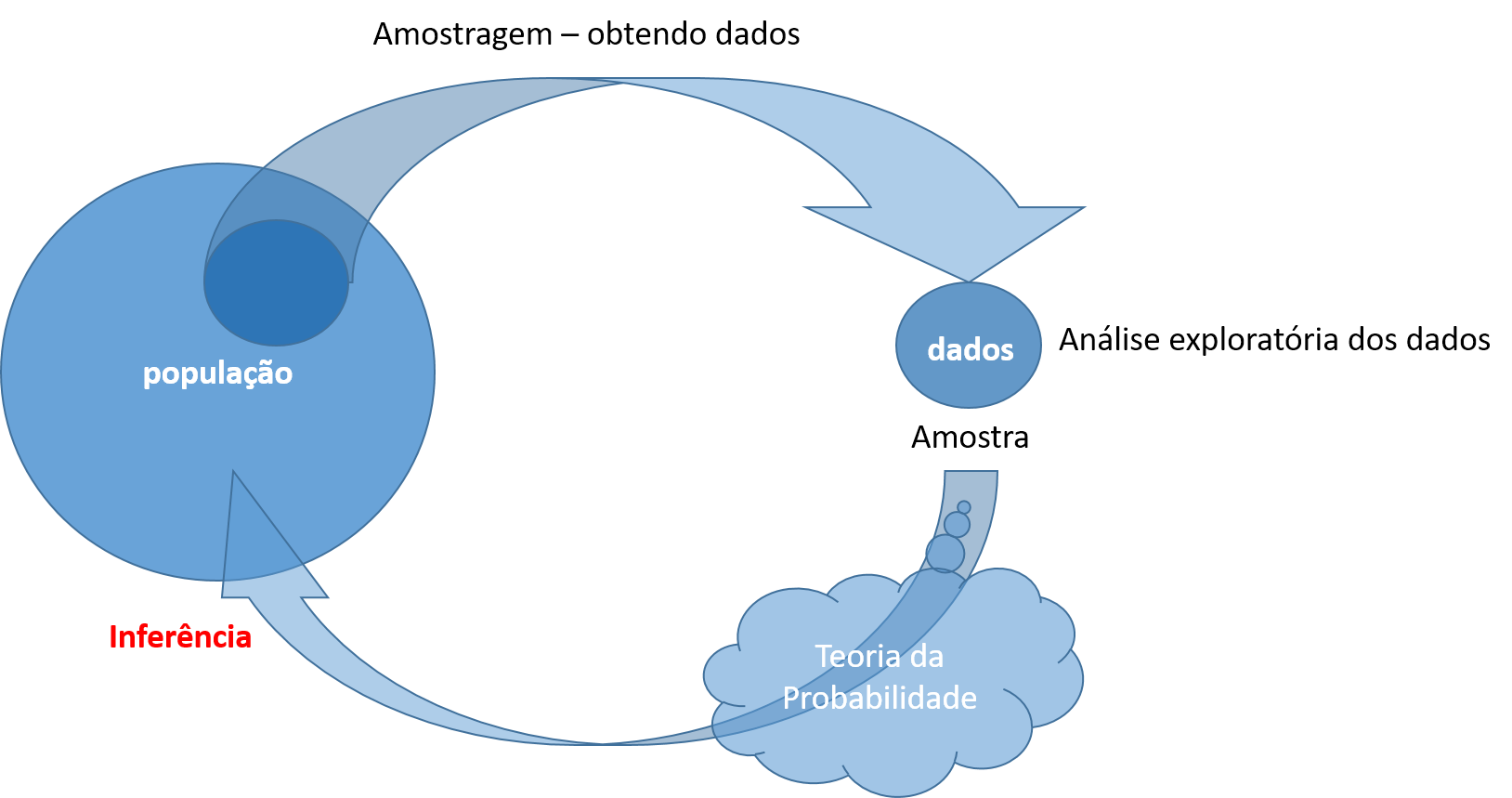
Uma vez coletada uma amostra podemos realizar a análise exploratória dos dados e iniciar o processo de inferência estatística, ou seja inferir a respeito dos parâmetros populacionais (\(\mu\), \(p\), \(\sigma^2\), \(\sigma\), etc..) a partir da amostra.
Neste tópico vamos introduzir a notação generalizada de parâmetro populacional como \(\Theta\), assim podemos representar qualquer parâmetro acima mencionado. A notação que será utilizada para o estimador do parâmetro será \(\hat{\Theta}\)
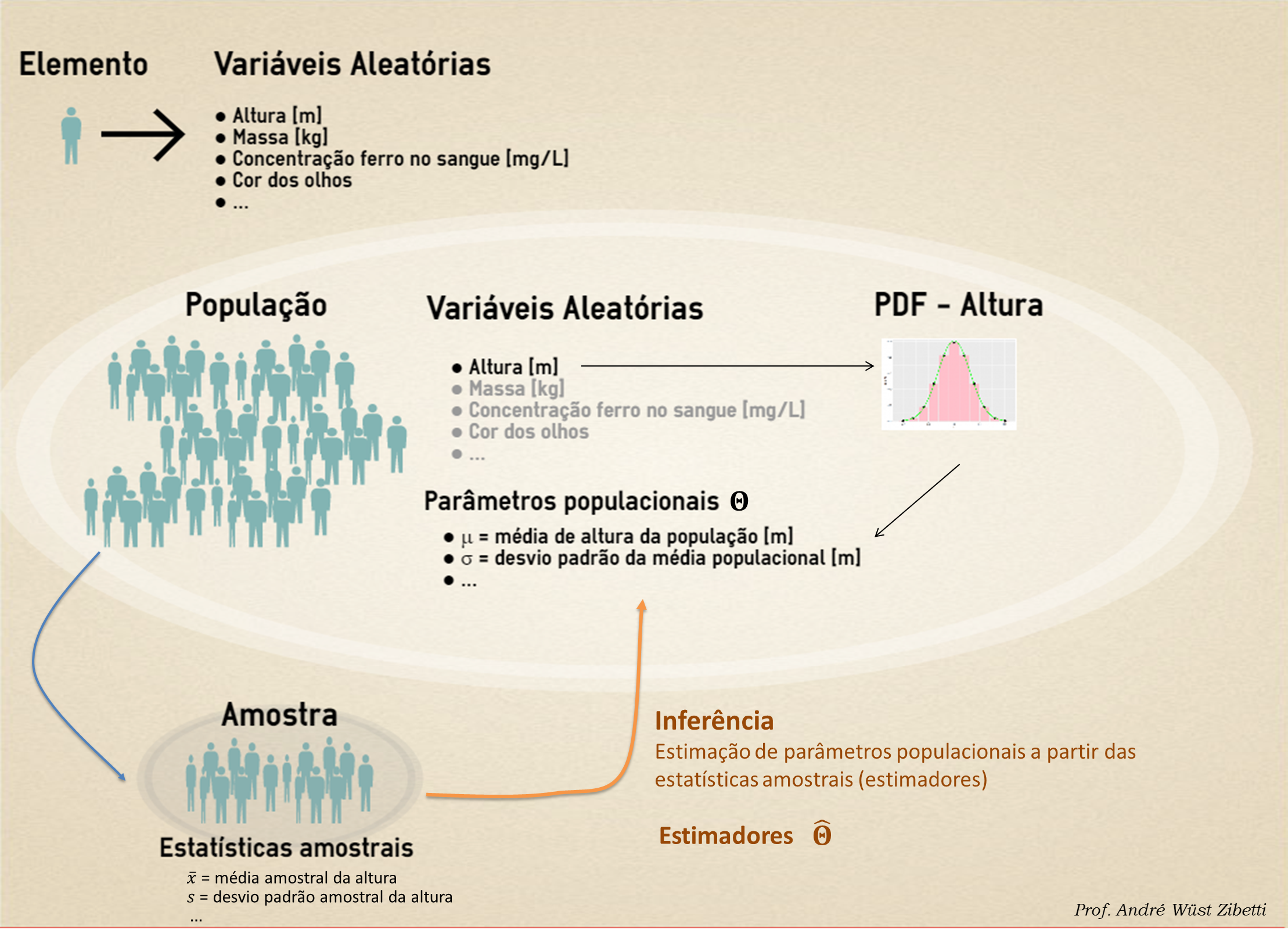
Para entender esse processo devemos ter em mente aquilo que estudamos a respeito de Teoria de Probabilidade, em especial aos resultados obtidos na teoria relacionada aos limites e distribuições amostrais.
Uma vez que compreendemos esses resultados da teoria da probabilidade estamos aptos a pensar a respeito do procedimento de inferência estatística, pois sabemos agora, a partir dessa teoria quais são as margens de erro e a variabilidade envolvida na coleta de uma amostra e subsequente determinação das estatística a fim de compara-las com os parâmetros populacionais, que na prática, são desconhecidos. Dessa forma iremos inferir quais são, ou melhor, que faixa de valores podem incluir os verdadeiros parâmetros populacionais em termos de probabilidade.
Para este procedimento devemos desenvolver (a partir de algum método, método dos momentos MM ou método da máxima verossimilhança MVS) que variáveis aleatórias seriam boas estimadoras (\(\hat{\Theta}\)) dos parâmetros populacionais (\(\Theta\)).
Neste contexto algumas abordagens dentro da Teoria da Probabilidade nos auxiliam na compreensão prática deste processo. A primeira abordagem é aquela que iremos desenvolver neste conteúdo que se refere a inferência clássica, que considera o parâmetro populacional como uma constante, por exemplo \(\mu = 10\), ou \(\Theta = 10\). Outra abordagem vem da inferência Bayesiana que considera o parâmetro populacional como uma variável aleatória, e consequentemente, com uma distribuição de probabilidade.
Vamos agora estudar quais são os estimadores obtidos pelos métodos (MM e MVE) e suas propriedades.
Estimadores \(\hat{\Theta}\) e suas propriedades
Os estimadores devem ter algumas propriedades de interesse, para que os consideremos úteis (utilizável para inferir).
De forma bastante resumida, os estimadores devem ser:
- Estimadores não tendenciosos, ou seja, \(E[\hat{\Theta}] = \Theta\);
- Estimadores não tendenciosos e de variância mínima, ou seja dentre estimadores não tendenciosos, aquele que tiver a menor variância;
Assim se \(E[\hat{\Theta_1}] = \Theta\) e \(E[\hat{\Theta_2}] = \Theta\), então o de menor variância será o escolhido, por exemplo, se \(V(\hat{\Theta_1}) < V(\hat{\Theta_2})\), então \(\hat{\Theta_1}\) é um estimador não tendencioso e de variância mínima (ENTVM).
Dentre os estimadores pontuais obtidos, por exemplo, pelo método da máxima verossimilhança (MVS), temos:
Estimador da média populacional (\(\mu\)): \[ \begin{align} \overline{X} & = \frac{1}{n} \sum{X_i}\\ E[\overline{X}] & = \mu \end{align} \] Estimador da proporção populacional (\(p\)): \[ \begin{align} \hat{P} & = \frac{1}{n} \sum{X_i}\\ E[\hat{P}] & = p \end{align} \] Estimador da variância populacional (\(\sigma^2\)): \[ \begin{align} S^2 & = \frac{1}{n-1} \sum{(X_i - \overline{X})^2}\\ E[S^2] & = \sigma^2 \end{align} \]
Estimação Intervalar e o desenvolvimento do intervalo de confiança (IC)
Neste tópico vamos focar na construção do intervalo de confiança para o parâmetro populacional, média (\(\mu\)), quando, hipotéticamente, a variância é conhecida (\(\sigma^2\)).
Suponha o seguinte exemplo:
Dado \(X_1, X_2, ..., X_n\), que é uma amostra aleatória de tamanho (\(n\)) de uma distribuição normal, \(X \sim N(\mu,\sigma^2)\), onde a \(\mu\) é desconhecida e \(\sigma^2\) conhecida.
Sabemos que a \(\mu\) pode ser estimada por \(\overline{X}\) (estimador pontual, distribuição amostral e lei dos grandes números).
Ao mesmo tempo que \(\overline{X}\) é um estimador com boas propriedades, reconhecemos que a estimativa (\(\overline{x}\)) está sujeita à um erro aleatório, o que faz com que o processo de estimação apresente o seguinte resultado:
\[ \overline{x} = \mu \pm \epsilon \] Isso ocorre pois não sabemos o quão próximo está a estimativa (\(\overline{x}\)) do verdadeiro parâmetro populacional (\(\mu\)). Assim temos interesse e obter uma forma de quantificar e entender esse erro aleatório (\(\epsilon\)). Para isso vamos iniciar o processo de construção do intervalo de confiança a partir do entendimento do comportamento do estimador (\(\overline{X}\)), no presente caso, para a média.
Temos que, a partir dos resultados do Teorema Central do Limite,
\[ \frac{\overline{X} - \mu}{\sigma/\sqrt{n}} \sim N(0,1) \]
Onde para uma probabilidade (\(1-\alpha\)), podemos calcular o quantil \(z_{\alpha/2}\). Então,
\[ \mathbb{P}\left( -z_{\alpha/2} \le \frac{\overline{X} - \mu}{\sigma/\sqrt{n}} \le z_{\alpha/2} \right) = 1 - \alpha \] Por exemplo para (\(1-\alpha\)) = 0.95, o quantil é \(z_{\alpha/2} = 1.96\).
library(nhstplot)
plotztest(z = 1.96, title = "N(0,1); 95 %", ylabel = "Densidade")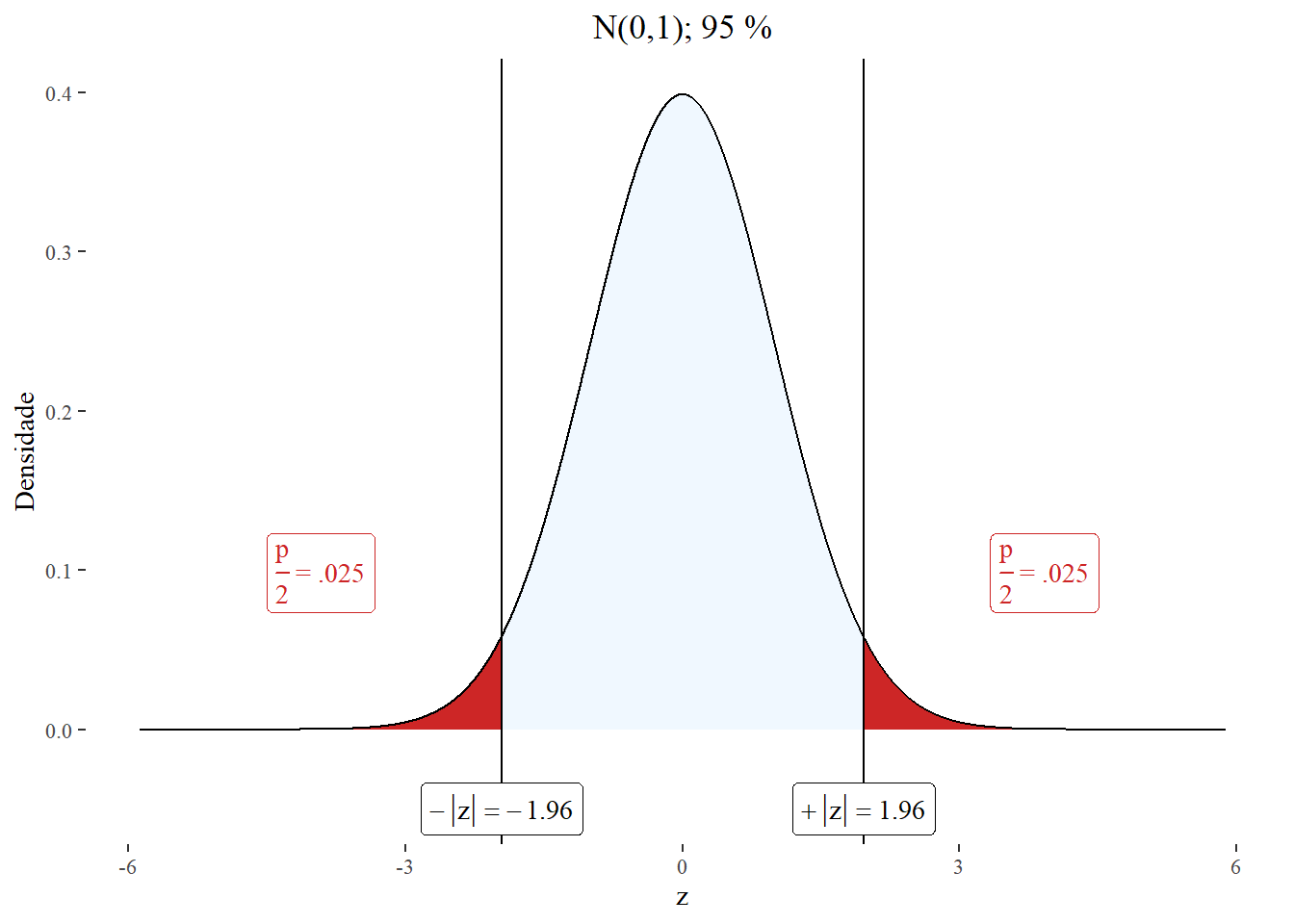
ou seja,
\[ \mathbb{P}\left( -1.96 \le \frac{\overline{X} - \mu}{\sigma/\sqrt{n}} \le 1.96 \right) = 0.95 \] Podemos afirmar que existe uma probabilidade de 0.95 da variável aleatória padronizada estar entre -1.96 e 1.96.
Dessa forma vamos continuar com nossa análise e a partir dessa expressão isolarmos o parâmetro \(\mu\).
Voltando a forma geral e manipulando as desigualdades equivalentes obtemos,
\[ \mathbb{P}\left( \overline{X} - z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \le \mu \le \overline{X} + z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \right) = 1 - \alpha \] Onde,
\[ \left[ \overline{X} - z_{\alpha/2}\frac{\sigma}{\sqrt{n}} ; \overline{X} + z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \right] \] é o intervalo (aleatório) de confiança \(100(1-\alpha)\) % para \(\mu\).
A quantidade \(1-\alpha\) é chamada de coeficiente de confiança, e \(\alpha\) é o nível de significância.
Se \(\overline{x}\) for a média amostral (ou seja, a estimativa do estimador \(\overline{X}\)) de uma amostra aleatória de tamanho \(n\), proveniente de uma população com variância conhecida \(\sigma^2\), um intervalo com \(100(1-\alpha)\) % de confiança para \(\mu\) é dado por, \[ \overline{x} - z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \le \mu \le \overline{x} + z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \]
O intervalo é muitas vezes escrito de forma compacta como: \[ \overline{x} \pm z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \]A interpretação da desigualdade é dada a seguir:
A interpretação do intervalo de confiança pode ser complicada e muitas vezes confundida por novatos no assunto. A forma de explicitarmos o intervalo de confiança é que esse intervalo é aleatória, e assim em \(100(1-\alpha)\) % das vezes o intervalo construido a partir da amostra poderá incluir o verdadeiro parâmetro populacional (\(\mu\)).
Para um coeficiente de confiança \(1-\alpha\) fixo, se \(n\) aumenta, então o intervalo de confiança se torna menor.
Para um tamanho de amostra \(n\) fixo, se \(1-\alpha\) aumenta, então o intervalo de confiança se torna maior.Note que o intervalo de confiança é aleatório, dessa forma dependendo da amostra que for retirada da população teremos uma dada média amostral (\(\overline{x}\)) e um desvio padrão (\(S\)). No caso em que se conheça o desvio padrão da população (\(\sigma\)) podemos facilmente construir o intervalo tendo como referência a distribuição normal padronizada, conforme deduzimos.
O seguinte Applet desenvolvido pela equipe do MIT Mathlet - Intervalo de confiança facilita o entendimento da distribuição amostral bem como a interpretação de um intervalo de confiança.
Intervalo de confiança para \(\mu\), com variância desconhecida \(\sigma^2\), amostra grande
Se \(\overline{x}\) for a média amostral (ou seja, a estimativa do estimador \(\overline{X}\)) de uma amostra aleatória de tamanho \(n > 40\), proveniente de uma população com variância desconhecida \(\sigma^2\), um intervalo com \(100(1-\alpha)\) % de confiança para \(\mu\) é dado por, \[ \overline{x} - z_{\alpha/2}\frac{S}{\sqrt{n}} \le \mu \le \overline{x} + z_{\alpha/2}\frac{S}{\sqrt{n}} \] onde,
\[ \frac{\overline{X} - \mu}{S/\sqrt{n}} \sim N(0,1) \]
O intervalo é muitas vezes escrito de forma compacta como:
\[ \overline{x} \pm z_{\alpha/2}\frac{S}{\sqrt{n}} \]Intervalo de confiança para \(\mu\), com variância desconhecida \(\sigma^2\), amostra pequena
Se \(\overline{x}\) for a média amostral (ou seja, a estimativa do estimador \(\overline{X}\)) de uma amostra aleatória de tamanho \(n < 40\), proveniente de uma população com variância desconhecida \(\sigma^2\), um intervalo com \(100(1-\alpha)\) % de confiança para \(\mu\) é dado por, \[ \overline{x} - t_{\alpha/2,n-1}\frac{S}{\sqrt{n}} \le \mu \le \overline{x} + t_{\alpha/2,n-1}\frac{S}{\sqrt{n}} \] onde a quantidade \(T\) segue uma distribuição t-student com \(v = n-1\) graus de liberdade
\[ T = \frac{\overline{X} - \mu}{S/\sqrt{n}} \sim t(n-1) \]
O intervalo é muitas vezes escrito de forma compacta como:
\[ \overline{x} \pm t_{\alpha/2,n-1}\frac{S}{\sqrt{n}} \]Intervalo de confiança para a proporção \(p\) de uma população, amostra grande
Se \(\hat{p}\) for a proporção amostral (ou seja, a estimativa do estimador \(\hat{X}\)) de uma amostra aleatória de tamanho \(n > 40\), proveniente de uma população, um intervalo com \(100(1-\alpha)\) % de confiança para \(p\) é dado por, \[ \hat{p} - z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \le p \le \hat{p} + z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \] onde,
\[ \frac{\hat{P} - p}{\sqrt{\frac{p(1-p)}{n}}} \sim N(0,1) \]
O intervalo é muitas vezes escrito de forma compacta como:
\[ \hat{p} \pm z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \]Intervalo de confiança para a diferença de médias \(\mu_1 - \mu_2\), variâncias conhecidas (\(\sigma^2_1\) e \(\sigma^2_2\))
Este conteúdo está disponível por meio da Licença Creative Commons 4.0
