Processos de chegada
Distribuição de Poisson
Esta é uma distribuição associada a “eventos raros”. As razões para isso se tornarão mais claras a medida que a aplicação desse modelo for descrita. Os eventos podem ser:
- acidentes automotivos
- erros de digitação
- chegada de um cliente em um banco
- entre outros eventos…
Seja \(\lambda\) a média de eventos em um intervalo de tempo, área ou volume, ou ainda a taxa média de ocorrência por unidade medida. Seja a variável aleatória \(X\) a contagem do número de eventos ocorrendo no intervalo. Então sob certas condições pode ser demonstrado que,
\[ p_X(x) = \mathbb{P}(X=x)=e^{-\lambda}\frac{\lambda^{x}}{x!} \quad x=0,1,2,3 ...\\ \]
\[ E[X]=\lambda=np\\ p=\frac{\lambda}{n}\\ V(X)=\lambda\\ \]
A distribuição de Poisson é aplicável quando o número de possíveis ocorrências discretas é muito maior do que o número médio de ocorrências em um determinado intervalo de tempo ou espaço. O número de possíveis ocorrências, muitas vezes não se sabe exatamente. Os resultados devem ocorrer de forma aleatória, ou seja, totalmente por acaso e da probabilidade de ocorrência não deve ser afectado por se ou não os resultados ocorrido anteriormente, de modo que as ocorrências são independentes. Em muitos casos, embora possamos contar as ocorrências, como a de uma tempestade, não podemos contar as não ocorrências correspondentes. (Nós não podemos contar “não-tempestades”!).
A probabilidade de um evento ocorrendo em um determinado subintervalo é aproximadamente \(\lambda/n\).
A probabilidade de dois ou mais eventos ocorrerem em qualquer subintervalo tende a zero \((0)\).
As ocorrências em subintervalos mutuamente exclusivos são indepedentes.
Dado um experimento aleatório \(e\), de acordo com a v.a.d. \(X\):
- Seja \(X\) o número de partículas contaminadas no intervalo de comprimento.
- Seja \(X\) o número de chamadas para uma troca de telefone no intervalo de tempo.
- Seja \(X\) o número de falhas no intervalo de área.
- Seja \(X\) o número de estrelas em um dado volume de espaço.
- Seja o experimento a observação do número de micro-organismos em uma amostra padrão de sangue, onde \(X\) representa o número de micro-organismos em qualquer amostra, e \(n\) o número de amostras estudadas.
- Seja o experimento a observação do número de partículas alpha emitidas durante cada sucessivo intervalo de \(t\) segundos. O número de tais intervalos será \(n\), e \(X\) será o número de partículas durante o 1º, 2º e nº-ésimo intervalo.
- Observando o número de bolhas (falhas) em cada uma das \(n\) superfícies, \(X\) representa o número de bolhas (falhas) em qualquer uma das superfícies.
- …
Dedução
A dedução do modelo de Poisson é dada a partir do modelo binomial para o caso onde temos infinitas tentativas. Ou seja a distribuição de Poisson é um caso limite da binomial, que se desenvolve quando o número de tentativas \(n\) aumenta indefinidamente, enquanto o produto \(\lambda=np\), que é o valor esperado do número de sucessos das tentativas, permanece constante. Dessa forma considere a PMF binomial:
\[p(x)=\mathbb{P}(X=x)=\left(\begin{array}{c}n\\x\end{array}\right)p^x(1-p)^{n-x}.\]
\[p(x)=\mathbb{P}(X=x)=\frac{n!}{x!(n-x)!}p^x(1-p)^{n-x}.\]
que pode ser reescrita como,
\[\mathbb{P}(X=x)=\frac{n!}{x!(n-x)!}p^x\frac{n^x}{n^x}\left(1-\frac{np}{n}\right)^{n-x}=\frac{n!}{x!(n-x)!}\frac{(np)^x}{n^x}\left(1-\frac{np}{n}\right)^{n-x}\]
\[\mathbb{P}(X=x)=\frac{(np)^x}{x!}\frac{n!}{n^x(n-x)!}\left(1-\frac{np}{n}\right)^{n-x}\]
\[\mathbb{P}(X=x)=\frac{(np)^x}{x!}\frac{n!}{n^x(n-x)!}\left(1-\frac{np}{n}\right)^{n}\left(1-\frac{np}{n}\right)^{-x}\]
sendo \(\lambda = np\),
\[\mathbb{P}(X=x)=\frac{\lambda^x}{x!}\frac{n!}{n^x(n-x)!}\left(1-\frac{\lambda}{n}\right)^{n}\left(1-\frac{\lambda}{n}\right)^{-x}\]
A expressão pode ser separada com o propósito de avaliarmos os seus limites quando \(lim(n\rightarrow\infty)\). Os limites em questão são,
\[lim(n\rightarrow\infty)\frac{n!}{n^x(n-x)!}= lim(n\rightarrow\infty)\left\{\frac{n(n-1)\cdots(n-x+1)}{x!}\right\}=1\]
\[lim(n\rightarrow\infty)\left(1-\frac{\lambda}{n}\right)^{n}=e^{-\lambda}\]
\[lim(n\rightarrow\infty)\left(1-\frac{\lambda}{n}\right)^{-x}=1\]
Reconstruindo a expressão vemos que a PMF binomial tem a seguinte forma limite,
\[\lim_{n\rightarrow \infty}\mathbb{P}(X=x)=\frac{e^{-\lambda}\lambda^x}{x!}.\]
que é a PMF de Poisson.
Observações quanto à dedução
No que se refere as condições matemáticas do parâmetro \(\lambda = np\), de um número infinito de tentativas (\(n\rightarrow \infty\)) e uma probabilidade infinitesimal (\(p\rightarrow 0\)) nunca são obtidos em problemas práticos. Assim para o propósito prático a distribuição de Poisson pode ser aplicada quando,
- \(n\ge50\) e se o múmero de vezes que um evento em particular for pequeno
- \(p\le0.1\) e se o número médio de vezes que os eventos ocorrem tem um valor finito \(\lambda=np\).
A função de Poisson pode ser derivada considerando uma especificação para o que chamamos de processo de emissão ou processo de chegada. Imagine um contador Geiger, que registra sucessivos impactos de uma particula radioativa (alpha) sobre uma fino filme metálico. A PMF descreve a probabilidade de \(x\) impactos ou chegadas em um intervalo de tempo \((0,t]\). Algumas condições são impostas, como:
- A probabilidade de uma única chegada em um pequeno intervalo de tempo tende a \(\lambda t\).
- A probabilidade de mais de uma chegada naquele intervalo de tempo é insignificante.
- A probabilidade de uma chegada durante um intervalo de tempo é independente de qualquer ocorrência em períodos anteriores.
Exemplos de ocorrências em que a distribuição de Poisson é utilizada incluem a contagem de um contador Geiger, colisões de carros em um cruzamento específico sob condições específicas, falhas em um casting, chamadas de telefone a um telefone em particular entre outras. Para a distribuição de Poisson ser aplicável a esses resultados, eles devem ocorrer de forma aleatória.
1º aplicação da distribuição O primeiro registro do uso da distribuição de Poisson para tratar populações tento as propriedades listadas acima é atribuído a Bortkewitsch que estudou a frequencia de mortes devido ao “coice de um cavalo” de dez (10) corpos, membros da Cavalaria Prussiana, durante o período de 20 anos.
Exemplo Poisson 1
Um vendendor de seguro de vida vende em média 3 seguros de vida por semana. Utilize a distribuição de Poisson para calcular em que uma dada semana ele irá vender,
- Alguns seguros.
- Dois ou mais seguros, porém menos que 5.
- Assumindo que existam 5 dias úteis por semana, qual é a probabilidade de que um dado dia ele venda um seguro?
Solução
De acordo com o enunciado temos \(\lambda = 3\)
- Alguns seguros.
Alguns seguros significa “1 ou mais seguros”. Para resolvermos esse problema devemos utilizar o complemento.
\[ \mathbb{P}(X > 0)= 1 - \mathbb{P}(X = 0)\\ \mathbb{P}(X > 0)= 1 - \frac{e^{-\lambda}\lambda^x}{x!}\\ \mathbb{P}(X > 0)= 1 - \frac{e^{-3}3^0}{0!} = 0.9502129 \]
lambda = 3
x = 0
p_x = dpois(x,lambda)
1 - p_x[1] 0.9502129Exemplo Poisson 2
Um problema mais recente que o anterior envolvendo a distribuição de Poisson era dentro da área de telefonia (1926). O problema era baseado nos seguintes dados.
## Importando os dados para o R
tel = read.csv("telefone.csv")| Conexoes.erradas | Frequencia.observada |
|---|---|
| 0 | 0 |
| 1 | 0 |
| 2 | 1 |
| 3 | 5 |
| 4 | 11 |
| 5 | 14 |
| 6 | 22 |
| 7 | 43 |
| 8 | 31 |
| 9 | 40 |
| 10 | 35 |
| 11 | 20 |
| 12 | 18 |
| 13 | 12 |
| 14 | 7 |
| 15 | 6 |
| 16 | 2 |
## Importando os dados para o R
con = read.csv("T_ConexoesErradas.csv")| x = numero de conexoes erradas por periodo | Frequencia Observada | Total de conexoes erradas |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 2 | 1 | 2 |
| 3 | 5 | 15 |
| 4 | 11 | 44 |
| 5 | 14 | 70 |
| 6 | 22 | 132 |
| 7 | 43 | 301 |
| 8 | 31 | 248 |
| 9 | 40 | 360 |
| 10 | 35 | 350 |
| 11 | 20 | 220 |
| 12 | 18 | 216 |
| 13 | 12 | 156 |
| 14 | 7 | 98 |
| 15 | 6 | 90 |
| 16 | 2 | 32 |
| 17 | 0 | 0 |
A taxa ou número médio de conexões erradas por período \(\lambda\) é igual a:
\[ \lambda = \frac{2334}{267}= \frac{Total \space de \space conexões \space erradas}{Total \space de \space frequencias \space observadas}=8.741573 \]
lambda = sum(con[3])/sum(con[2])
lambda[1] 8.741573A partir desse ponto podemos calcular as frequências teóricas de conexões erradas fazendo uso do modelo de Poisson.
lambda = 8.741573
x = seq(0,30,1)
p_x = dpois(x,lambda)
plot(x,p_x,type='h',xlab='Números de conexões erradas por período',ylab=expression(p[X](x)))
points(x,p_x,col=2)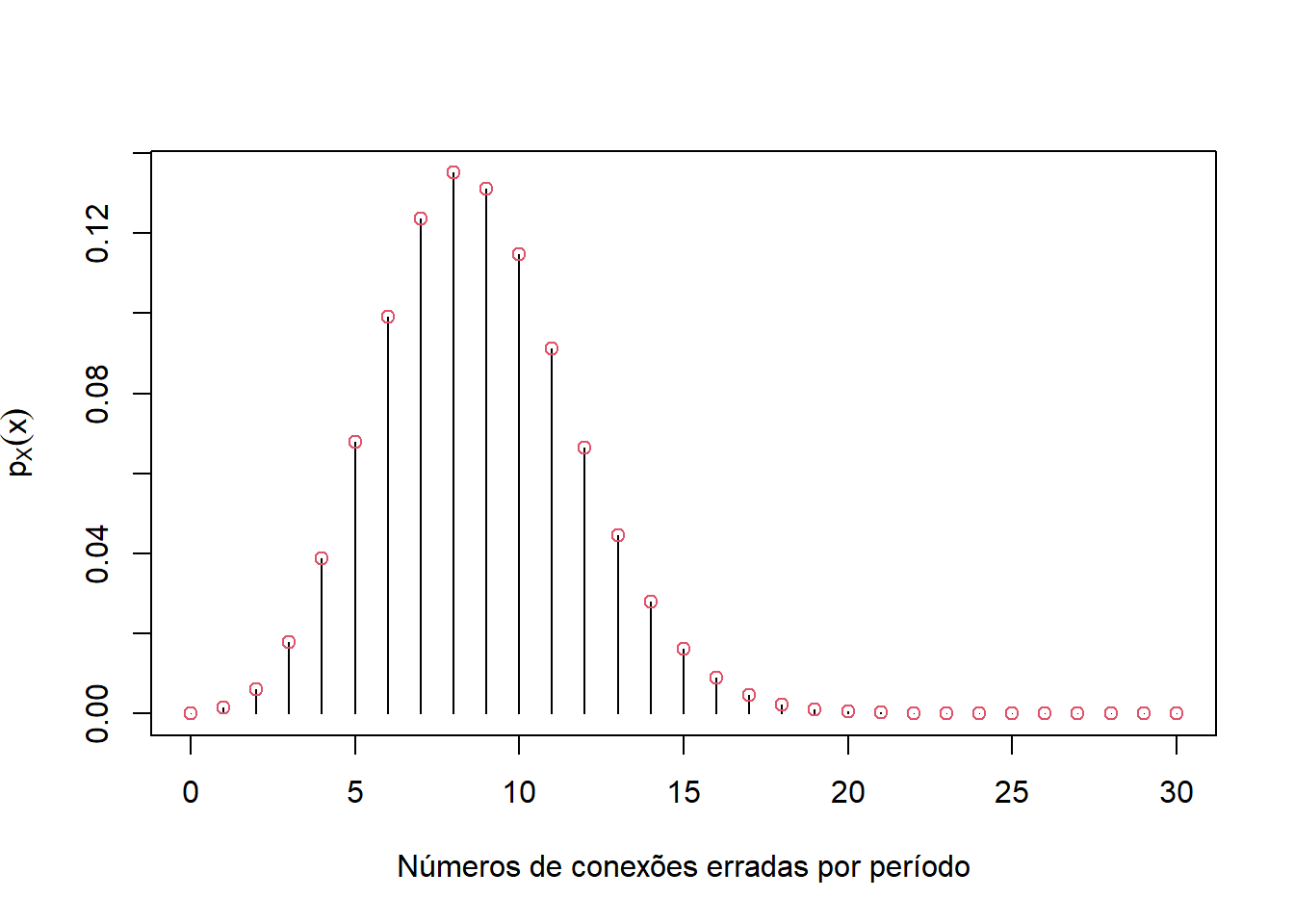
dx = data.frame(x, p_x) # agrupa os vetores x e p_x em um data frame
dx =round(dx,digits=4) # arredonda os valores do data frame
dx x p_x
1 0 0.0002
2 1 0.0014
3 2 0.0061
4 3 0.0178
5 4 0.0389
6 5 0.0680
7 6 0.0990
8 7 0.1237
9 8 0.1351
10 9 0.1313
11 10 0.1147
12 11 0.0912
13 12 0.0664
14 13 0.0447
15 14 0.0279
16 15 0.0163
17 16 0.0089
18 17 0.0046
19 18 0.0022
20 19 0.0010
21 20 0.0004
22 21 0.0002
23 22 0.0001
24 23 0.0000
25 24 0.0000
26 25 0.0000
27 26 0.0000
28 27 0.0000
29 28 0.0000
30 29 0.0000
31 30 0.0000A frequencia teórica calculada é dada por:
\[ Frequencia \space teorica = (Total \space Frequencias \space Observadas)p_X(x) = 267p_X(x) \]
Frequencia_teorica = 267*p_x[1:17]
Frequencia_observada = con$`Frequencia Observada`[1:17]
valores_x = x[1:17]
fr = data.frame(valores_x, Frequencia_observada ,Frequencia_teorica) # agrupa os vetores em um data frame
fr=round(fr,digits=1)
colnames(fr) = c("x", "Frequencia Observada","Frequencia Teorica")
kable(fr,align = 'c')| x | Frequencia Observada | Frequencia Teorica |
|---|---|---|
| 0 | 0 | 0.0 |
| 1 | 0 | 0.4 |
| 2 | 1 | 1.6 |
| 3 | 5 | 4.8 |
| 4 | 11 | 10.4 |
| 5 | 14 | 18.1 |
| 6 | 22 | 26.4 |
| 7 | 43 | 33.0 |
| 8 | 31 | 36.1 |
| 9 | 40 | 35.0 |
| 10 | 35 | 30.6 |
| 11 | 20 | 24.3 |
| 12 | 18 | 17.7 |
| 13 | 12 | 11.9 |
| 14 | 7 | 7.4 |
| 15 | 6 | 4.3 |
| 16 | 2 | 2.4 |
Note que a frequencia teórica apresenta valores quebrados, o correto são número inteiros, dessa foi arredondado para 1 dígito significativo, como critério de comparação.
Plotando as frequências teóricas vs as frequências observadas.
# Set bar fill to white, border to green
barplot(Frequencia_observada, col = "white", border ="green",names.arg = as.character(valores_x))
# Set bar fill to white, border to red and add to prior plot
barplot(Frequencia_teorica, col = "white", border = "red", add = TRUE) 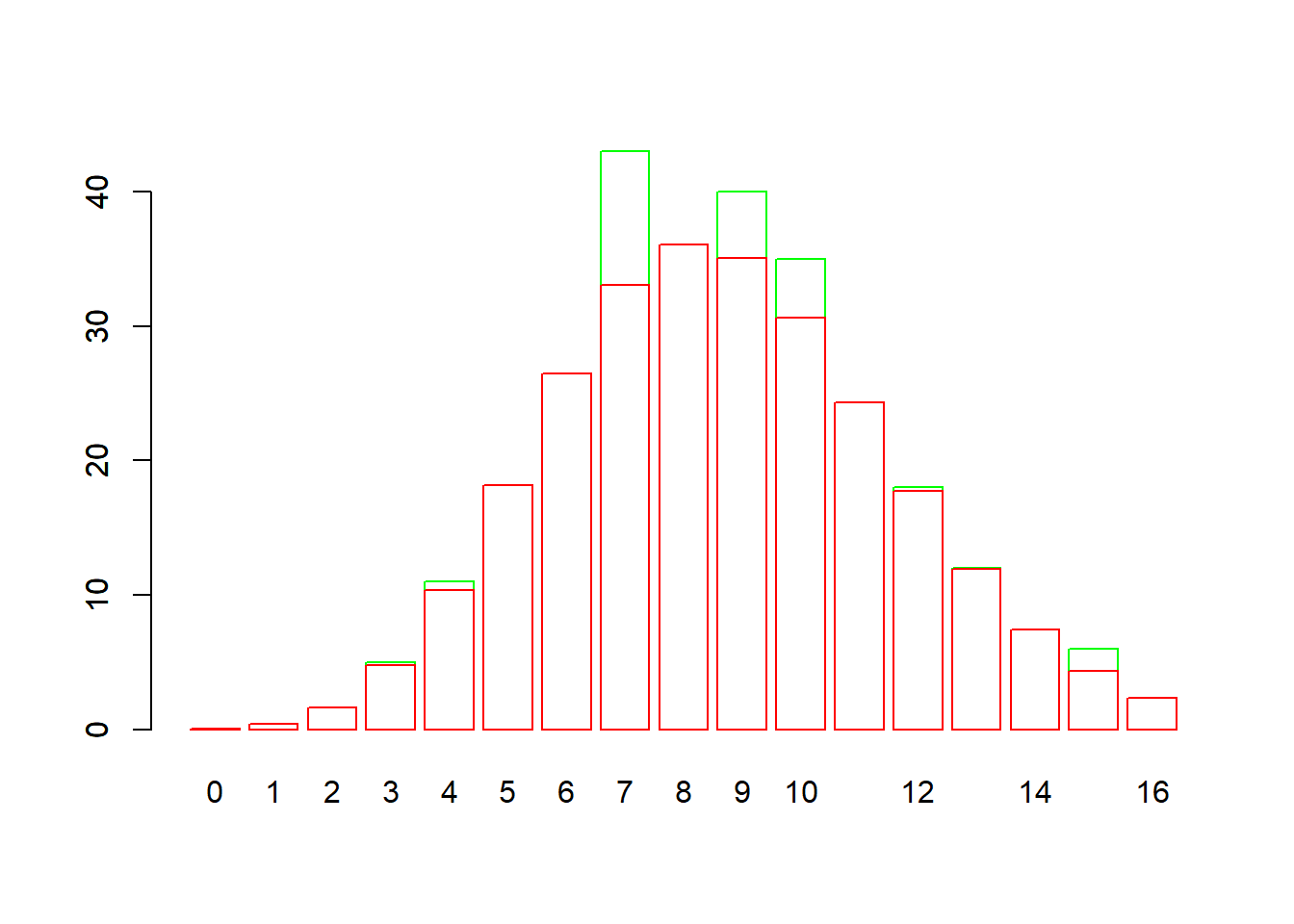
par(mfrow=c(2,1))
# Set bar fill to white, border to green
barplot(Frequencia_observada, col = "white", border ="green", main="Frequencia Observada",names.arg = as.character(valores_x))
# Set bar fill to white, border to red and add to prior plot
barplot(Frequencia_teorica, col = "white", border = "red", main="Frequencia Teorica",names.arg = as.character(valores_x)) 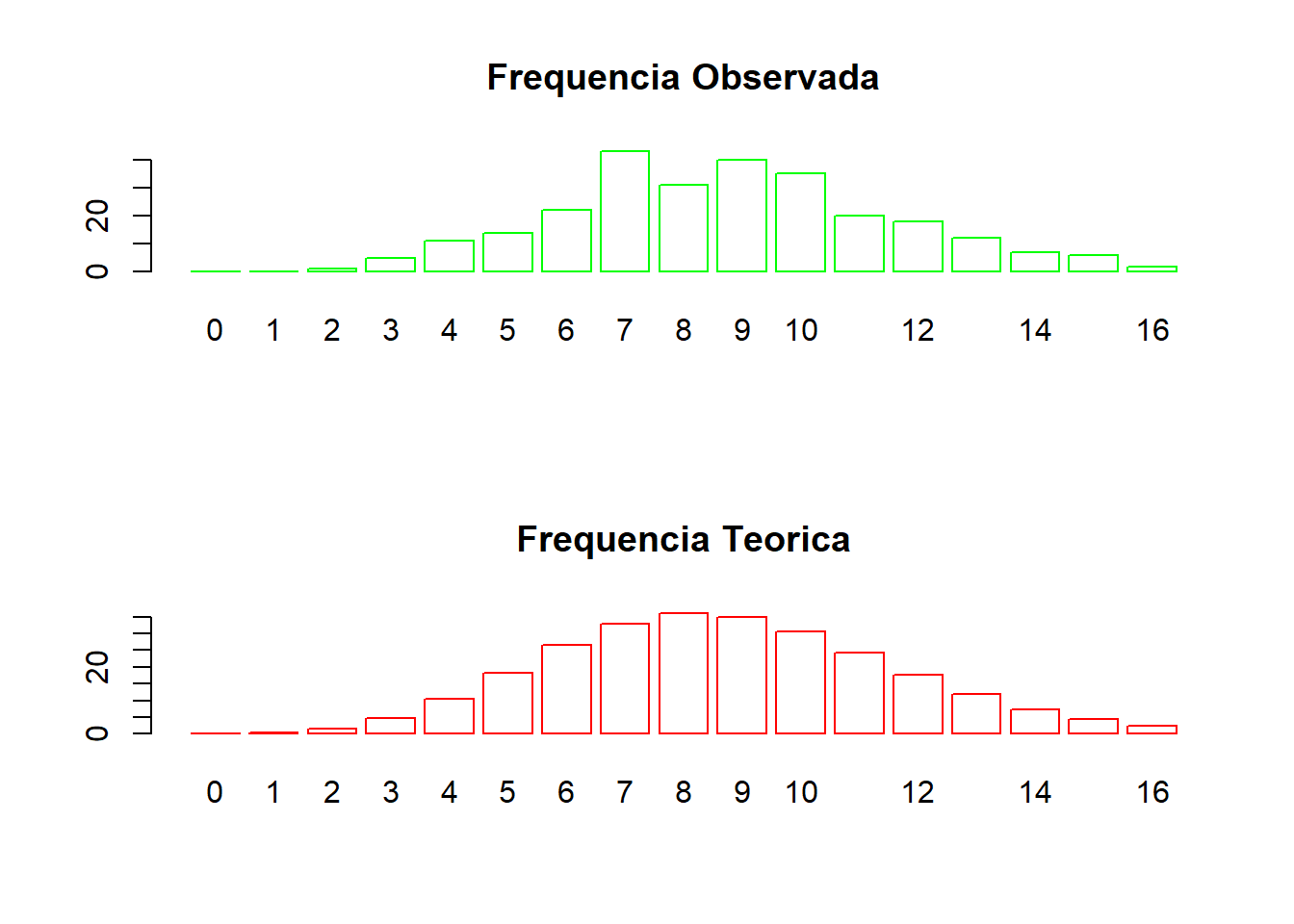
Podemos observar que o número de conxões erradas segue uma distribuição de Poisson com parâmetro \(\lambda\), onde as frequências observadas quando comparadas pelas frequências teóricas concordam em valores e escala.
As probabilidade calculadas a partir da distribuição de Poisson podem ser utilizadas para predizer a ocorrência de conexões erradas e assim servirem como uma base para o melhoramento do sistema. O melhoramento desse sistema poderá compensar tais falhas evitando a ocorrência de conexoes erradas.
A efetividade das mudanças de engenharia pode ser avaliada em termos da mudança do parâmetro \(\lambda\), por exemplo.
Exemplo Poisson 3
Outra abordagem no cálculo da probabilidade de Poisson, onde \(x\) é o número de ocorrências de um evento em um intervalo de tempo ou espaço sob determinadas condições é dado por:
\[ p_X(x) = \mathbb{P}(X=x)=e^{-(\lambda t)}\frac{(\lambda t)^{x}}{x!}\\ \] onde \(t\) (em unidades de tempo, comprimento, área ou volume) é um intervalo de tempo ou espaço no qual os eventos ocorrem, e \(\lambda\) é a taxa média de ocorrência por unidade de tempo ou espaço.
Dessa forma, suponha, o número de meteoros encontrados por um sistem de radar em qualquer intervalo de 30-segundos sob determinadas condições é em média 1.81. Assuma que os meteoros apareçam aleatóriamente e independentemente.
- Qual é a probabilidade de que nenhum meteoro seja encontrado em um intervalo de um minuto (60-segundos)?
- Qual é a probabilidade de que sejam observados no mínimo cinco porém não mais que oito meteoros em dois minutos (120-segundos) de observação?
Solução
- Qual é a probabilidade de que nenhum meteoro seja encontrado em um intervalo de um minuto (60-segundos)?
\[ \lambda t = \frac{1.81 [meteoros]}{30[seg]}\frac{60[seg]}{1[min]} = 3.62 \frac{[meteoros]}{[min]} \] Assim, para um intervalo de um minuto, \((\lambda t) = 3.62\)
Para calcular a probabilidade temos:
\[ p_X(x) = \mathbb{P}(X=0)=e^{-3.62}\frac{3.62^{0}}{0!}=0.02678268\\ \]
lambda = 3.62
x = 0
p_x = dpois(x,lambda)
p_x[1] 0.02678268- Qual é a probabilidade de que sejam observados no mínimo cinco porém não mais que oito meteoros em dois minutos (120-segundos) de observação?
Para um intervalo de dois minutos temos: \[ \lambda t = \frac{1.81 [meteoros]}{30[seg]}\frac{120[seg]}{2[min]} = 7.24 \frac{[meteoros]}{[2 min]} \]
Para calcular a probabilidade:
\[ p_X(x) = \mathbb{P}(5 \le X \le 8)=\mathbb{P}(X=5)+\mathbb{P}(X=6)+\mathbb{P}(X=7)+\mathbb{P}(X=8)=0.5451062\\ \]
lambda = 7.24
x = seq(5,8,1)
p_x = dpois(x,lambda)
p_x[1] 0.1189103 0.1434851 0.1484046 0.1343062sum(p_x)[1] 0.5451062Exemplo Poisson 4
O número médio de colisões ocorrendo em uma semana durante os meses de verão em uma intersecção é de 2.00. Assuma que os pressupostos para a distribuição de Poisson são satisfeitas.
- Qual é a probabilidade de que nenhuma colisão ocorra em uma semana em particular?
- Qual é a probabilidade de que exatamemente uma colisão ocorra em uma semana em particular?
- Qual é a probabilidade de que exatamente duas colisões ocorram em uma semana em particular?
- Qual é a probabilidade de encontrar não mais do que duas colisões em uma semana?
- Qual é a probabilidade de encontrar exatamente duas colisões em um intervalo de duas semanas?
Solução
- Qual é a probabilidade de que nenhuma colisão ocorra em uma semana em particular?
\[ \lambda = 2.00 \frac{[colisoes]}{[semana]}\\ t = 1 [semana]\\ \lambda t= 2.00 \frac{[colisoes]}{[semana]}[semana] = 2.00 [colisoes]\\ \] Para calcular a probabilidade temos:
\[ p_X(x) = \mathbb{P}(X=0)=e^{-2.00}\frac{2.00^{0}}{0!}=0.1353353\\ \]
lambda = 2.00
x = 0
p_x = dpois(x,lambda)
p_x[1] 0.1353353- Qual é a probabilidade de que exatamemente uma colisão ocorra em uma semana em particular?
\[ p_X(x) = \mathbb{P}(X=1)=e^{-2.00}\frac{2.00^{1}}{1!}=0.2706706\\ \]
lambda = 2.00
x = 1
p_x = dpois(x,lambda)
p_x[1] 0.2706706- Qual é a probabilidade de que exatamente duas colisões ocorram em uma semana em particular?
\[ p_X(x) = \mathbb{P}(X=2)=e^{-2.00}\frac{2.00^{2}}{2!}=0.2706706\\ \]
lambda = 2.00
x = 2
p_x = dpois(x,lambda)
p_x[1] 0.2706706- Qual é a probabilidade de encontrar não mais do que duas colisões em uma semana?
\[ p_X(x) = \mathbb{P}(X \le 2)=\mathbb{P}(X=0)+\mathbb{P}(X=1)+\mathbb{P}(X=2) = 0.6766764\\ \]
lambda = 2.00
x = seq(0,2,1)
p_x = dpois(x,lambda)
p_x[1] 0.1353353 0.2706706 0.2706706sum(p_x)[1] 0.6766764- Qual é a probabilidade de encontrar mais de duas colisões em uma semana?
\[ p_X(x) = \mathbb{P}(X > 2)=1-\mathbb{P}(X \le 2) = 1 - 0.6766764 = 0.3233236\\ \]
lambda = 2.00
x = seq(0,2,1)
p_x = dpois(x,lambda)
1-sum(p_x)[1] 0.3233236- Qual é a probabilidade de encontrar exatamente duas colisões em um intervalo de duas semanas?
\[ \lambda = 2.00 [/semana]\\ t = 2 [semanas]\\ \lambda t= 2.00 [/semana] 2 [semana] = 4.00\\ \] Para calcular a probabilidade temos:
\[ p_X(x) = \mathbb{P}(X=0)=e^{-4.00}\frac{4.00^{2}}{2!}=0.1465251\\ \]
lambda = 4.00
x = 2
p_x = dpois(x,lambda)
p_x[1] 0.1465251Exemplo Poisson 5
A procura de um tipo particular de bomba para uma mina isolado é aleatória e independente de ocorrências anteriores, mas a procura média em uma semana (7 dias) é de 2,8 bombas. Outros suprimentos são ordenados todas as manhãs terça-feira e chegam semanalmente na sexta-feira de manhã. Na última terça-feira pela manhã apenas uma bomba estava em estoque, de modo que o almoxarifado pediu mais seis para receber na Sexta de manhã
- Encontre a probabilidade de que uma bomba estará no estoque na sexta-feira pela manhã quando o novo carregameto chegar?
\[ \lambda = 2.80 [/semana]\\ \lambda = 2.80 [7/dias] = 0.4 [dia]\\ t = 3 [dias]\\ \lambda t= 0.40 [/dia] 3 [dias] = 1.2\\ \] ***
Exemplo Poisson 5 - a finalizar
O número de defeitos na superfície de painéis de plástico usados no interior de um modelo de automóveis segue uma distribuição de Poisson, com uma média de 0.05 falhas por metro quadrado. Considere que nesse modelo de automóvel se utilizam 6 metros quadrados de painel.
a.Qual a probabilidade de não haver qualquer defeito na superfície do painel de um automóvel desse modelo? b.Qual é o número médio e o desvio padrão de defeitos num conjunto de 10 automóveis desse modelo? c.Num conjunto de 10 automóveis vendidos a uma companhia de aluguer, qual será a probabilidade de que no mínimo dois automóveis tenham pelo menos um defeito na superfície? d.Considere que já foram inspeccionados 4m² do painel de um determinado automóvel e que nessa área foi encontrado um defeito. Qual a probabilidade de ser encontrado pelo menos mais um defeito na área restante do painel? e.Após um ajuste no processo de fabrico dos painéis, verificou-se que 85% dos automóveis saíam sem apresentar qualquer defeito na superfície do painel. Nestas novas condições, calcule a probabilidade de um determinado automóvel apresentar mais de dois defeitos na superfície do painel.
Solução
a.Qual a probabilidade de não haver qualquer defeito na superfície do painel de um automóvel desse modelo?
b.Qual é o número médio e o desvio padrão de defeitos num conjunto de 10 automóveis desse modelo?
c.Num conjunto de 10 automóveis vendidos a uma companhia de aluguel, qual será a probabilidade de que no mínimo dois automóveis tenham pelo menos um defeito na superfície?
Exemplo Poisson 6 - a finalizar
A empresa STEEL produz cabos de aço para a construção civil. De acordo com dados históricos da produção, sabe-se que os cabos produzidos apresentam defeitos seguindo uma distribuição de Poisson, com média de 0,07 defeitos por metro de cabo
- Qual é a probabilidade de um cabo de 10 metros de comprimento ter pelo menos 2 defeitos?
- Qual é o número médio de defeitos que se espera encontrar em 10 metros de comprimento de fio?
- De um grande lote de cabos de 2 metros de comprimento é retirada uma amostra de 10 unidades para averiguação da qualidade. O lote será classificado como de qualidade “excelente” somente se nenhum dos 10 cabos apresentar defeito. Caso contrário, o lote é classificado como de qualidade “razoável”. Qual é a probabilidade do lote ser classificado como de qualidade “razoável”?
- A empresa STEEL tem a possibilidade de vender o lote de cabos mencionado na alínea acima para dois clientes distintos. O cliente A está disposto a pagar 17.500 reais pelo lote sem qualquer análise prévia. O cliente B está disposto a pagar 22.000 reais se após averiguação da qualidade for constatado que o lote é de qualidade “excelente”, porém, se for constatado que é de qualidade “razoável”, está disposto a pagar 16.000. Para qual cliente a empresa deve vender o lote? Justifique a resposta.
Exemplo Poisson 7 - a finalizar
Uma máquina que funciona em tempo contínuo tem, em média, duas falhas por cada turno de 8 horas de funcionamento. Para efeitos práticos, pode-se considerar que as falhas são reparadas instantaneamente. Se numa oficina estiverem funcionando em simultâneo 20 máquinas daquele tipo, calcule:
- a probabilidade de ocorrerem 3 falhas nos últimos 10 minutos de um turno;
- o valor esperado e a variância do número global de falhas por hora.
Exemplo Poisson 8 - a finalizar
Num processo de fabricação de placas de vidro produzem-se pequenas bolhas que se distribuem aleatoriamente pelas placas, com uma densidade média de 0.4 bolhas/m2.
- Calcule a probabilidade de, numa placa de 1.5 x 3.0 m2, haver pelo menos uma bolha.
- Calcule a probabilidade de, num conjunto de 6 placas de 1.5 x 3.0 m2, haver pelo menos quatro sem bolhas.
Exemplo Poisson 9 - finalizar
Um entreposto, com capacidade para armazenar 80 toneladas de cimento, é abastecido por um trem, que o enche durante a noite. Ao entreposto dirigem-se diariamente caminhões com capacidade para transportar 20 toneladas, de acordo com uma distribuição de Poisson com parâmetro λ = 3/dia. Admita que, se houver cimento, cada caminhão será carregado até o limite da sua capacidade.
- Determine o valor esperado da quantidade de cimento que é transportada diariamente pelos caminhões.
- Calcule o valor esperado da procura não satisfeita diariamente.
Este conteúdo está disponível por meio da Licença Creative Commons 4.0
