Soma de variáveis aleatórias
Soma de variáveis aleatórias
Como pudemos verificar no exposto no tópico anterior Teoremas Limites a soma de variáveis aleatórias independentes e identicamente distribuídas (i.i.d.) converge em uma distribuição normal, com certas propriedades (valor esperado e variância) que podem ser calculadas a partir das regras básicas do valor esperado e variância tais como:
- Valor Esperado
- \(E[c] = c\)
- \(E[cX] = cE[X]\)
- \(E[X + Y] = E[X] + E[Y]\)
- \(E[XY] = E[X]E[Y]\)
- \(E[aX + b] = aE[X]+b\)
- Variância
- Definição: \(V(X) = E[X^2] - E[X]^2 = E[X - E[X]]^2\)
- \(V(c) = 0\)
- \(V(cX) = c^2V(X)\)
- \(V(X + c) = V(X)\)
- \(V(X + Y) = V(X) + V(Y)\) se \(X\) e \(Y\) forem independentes
- \(V(X - Y) = V(X) + V(Y)\) se \(X\) e \(Y\) forem independentes
- \(V(X + Y) = V(X) + V(Y) + 2Cov(X,Y)\)
- \(V(X - Y) = V(X) + V(Y) - 2Cov(X,Y)\)
- \(V(\sum_{i}{X_i}) = \sum_{i}{V(X_i)} + 2 \sum \sum_{i<j}{Cov(X_i,X_j)}\)
- \(V(X) = Cov(X,X)\)
- Definição: \(V(X) = E[X^2] - E[X]^2 = E[X - E[X]]^2\)
- Covariância
- Definição: \(Cov(X,Y) = E[XY] - E[X]E[Y] = E[(X - E[X])(Y - E[Y])]\)
- Simetria: \(Cov(X,Y) = Cov(Y,X)\)
- Correlação
- Definição: \(\rho(X,Y) = \frac{Cov(X,Y)}{\sqrt{V(X)V(Y)}}\)
- Propriedades: \(-1 \le \rho(X,Y) \le 1\)
Um pergunta que poderíamos estar interessados em saber é o que ocorre com a soma de variáveis aleatórias que são independentes porém não são identicamente distribuidas? Qual seria a sua convergência (em forma)? E quais são os casos particulares?
Para responder essa questão vou recorrer à uma simulação usando o método de Monte-Carlo, explicitando alguns casos e simplesmente observando os resultados, sem de forma alguma, postular uma regra geral, assim como foi feito até aqui.
Quandos as variáveis aleatórias são simétricas
Dada a soma de variáveis aleatórias simétricas a soma dessas converge em uma distribuição normal, quando \(n+m > 10\) (onde n + m é o número total de v.a.s envolvidas).
Distribuição contínuas simétricas:
- Normal
- Uniforme
Seja \(X_1, ...,X_n\) uma sequência de v.a.s onde \(X_i \sim N(\mu,\sigma^2)\)
Seja \(Y_1, ...,Y_m\) uma sequência de v.a.s onde \(Y_i \sim U(a,b)\)
A soma de \(\sum_{i=1}^{n}{X_i} + \sum_{j=1}^{m}{Y_j}\) resulta em qual distribuição?
Caso 1:
- \(S = X_1 + Y_1\), onde \(n + m = 2\)
- \(X_i \sim N(5,2^2)\)
- \(Y_j \sim U(2,12)\)
par(mfrow=c(2,2))
X1 = rnorm(1000000,5,2)
Y1 = runif(1000000,2,12)
hist(X1, freq=FALSE, breaks=100, col="lightblue", main="X1")
hist(Y1, freq=FALSE, breaks=100, col="lightblue", main="Y1")
S_2 = X1 + Y1
hist(S_2, freq=FALSE, breaks=100, col="lightblue", main="S = X1 + Y1")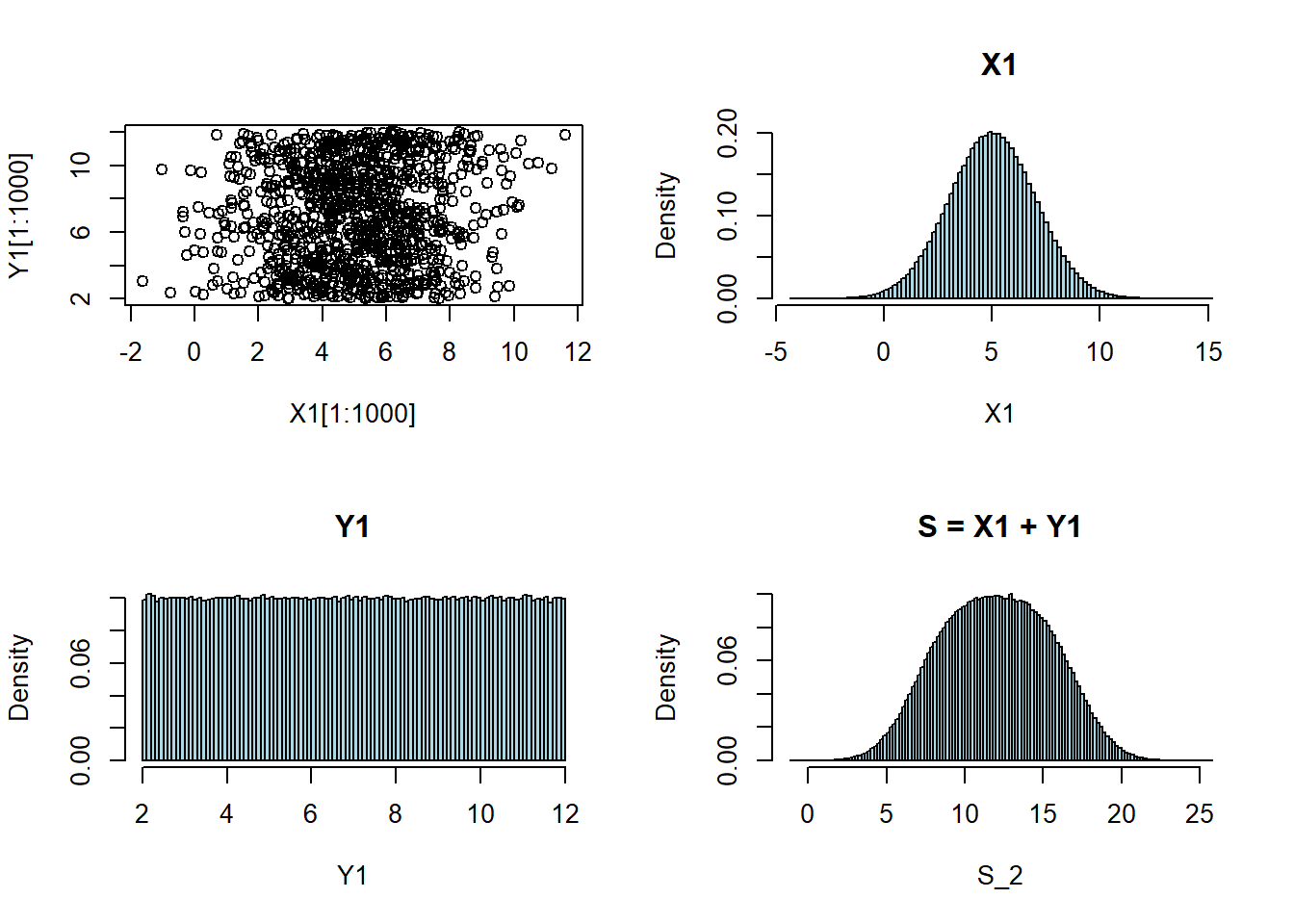
Caso 2:
- \(S = X_1 + X_2 + Y_1 + Y_2\), onde \(n + m = 4\)
- \(X_i \sim N(5,2^2)\)
- \(Y_j \sim U(2,12)\)
par(mfrow=c(3,2))
X1 = rnorm(1000000,5,2)
X2 = rnorm(1000000,5,2)
Y1 = runif(1000000,2,12)
Y2 = runif(1000000,2,12)
hist(X1, freq=FALSE, breaks=100, col="blue", main="X1")
hist(X2, freq=FALSE, breaks=100, col="blue", main="X2")
hist(Y1, freq=FALSE, breaks=100, col="blue", main="Y1")
hist(Y2, freq=FALSE, breaks=100, col="blue", main="Y2")
S_4 = X1 + X2 + Y1 + Y2
hist(S_4, freq=FALSE, breaks=100, col="blue", main="S = X1 + X2 + Y1 + Y2")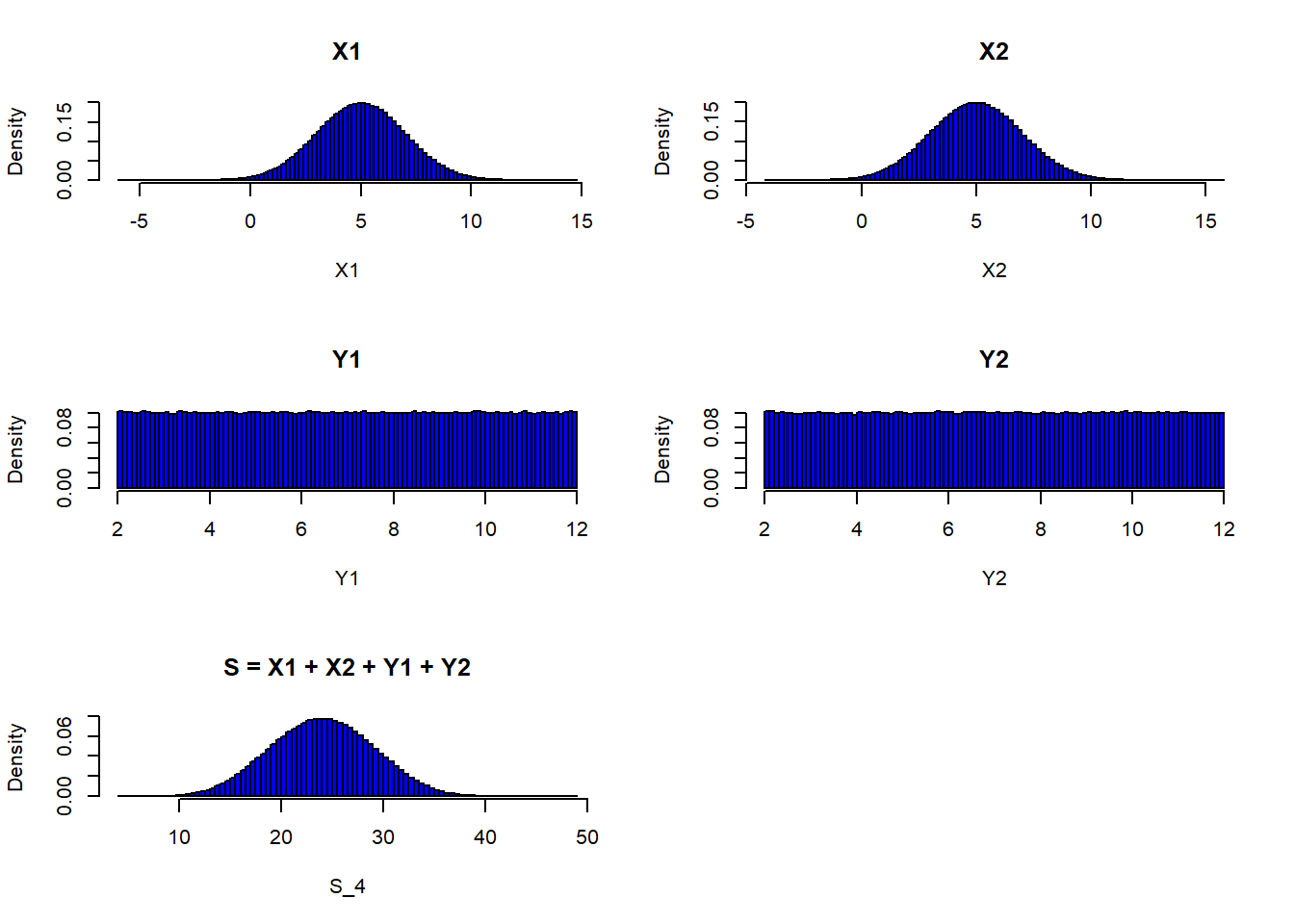
Propriedades calculadas pela regra do valor esperado:
- \(E[S_4] = E[X_1] +E[X_2] + E[Y_1] +E[Y_2] = 5 + 5 + 7 + 7 = 24\)
- \(V(S_4) = V(X_1) + V(X_2) + V(Y_1) + V(Y_2) = 2^2 + 2^2 + 8.33 + 8.33 = 24.66\)
Propriedades calculadas a partir da simulação
media = mean(S_4)
variancia = var(S_4)
cat("média = ", media, "\nvariância =", variancia)média = 23.99971
variância = 24.64106Note que os valores simulados (média \(E[X]\) e variância \(V(X)\)) são iguais aos valores obtidos teoricamente.
Podemos verificar o quão próximo estão as variáveis aleatórias \(S_2\) e \(S_4\) de uma distribuição normal em termos das medidas de assimetria e curtose.
library(moments)
sk_X1 = skewness(X1) # Se o valor da assimetria for = 0, então podemos afirmar que a distribuição é simétrica.
ku_X1 = kurtosis(X1) # Se o valor da curtose for = 3, então tem o mesmo achatamento que a distribuição normal (mesocúrticas).
sk_S_2 = skewness(S_2)
ku_S_2 = kurtosis(S_2)
sk_S_4 = skewness(S_4)
ku_S_4 =kurtosis(S_4)
cat("assimetria X1 = ", sk_X1, "\ncurtose X1 = ", ku_X1)assimetria X1 = 0.001303984
curtose X1 = 2.998742cat("\nassimetria S_2 = ", sk_S_2, "\ncurtose S_2 = ", ku_S_2)
assimetria S_2 = -0.002741101
curtose S_2 = 2.447919cat("\nassimetria S_4 = ", sk_S_4, "\ncurtose S_4 = ", ku_S_4)
assimetria S_4 = 0.0007094178
curtose S_4 = 2.729313De acordo com os resultados numéricos acima podemos observar que a simetria das variáveis aleatórias \(X, S_2, S_4\) são similares, ou seja, são simétricas, e que a curtose se aproxima de uma normal a medida que \(m+n\) aumenta.
Quandos as variáveis aleatórias não são simétricas
Dada a soma de variáveis aleatórias simétricas a soma dessas converge em uma distribuição normal, quando \(n+m > 10\).
Distribuição contínuas não simétricas:
- Exponencial
- Beta
- LogNormal
- Erlang
- Gama
- Weibull
Soma de duas distribuições Beta
- \(S_{2a} = X_1 + Y_1\), onde \(n + m = 2\)
- \(X_i \sim Beta(\alpha = 2, \beta = 7)\)
- \(Y_j \sim Beta(\alpha = 7, \beta = 2)\)
par(mfrow=c(2,2))
X1 = rbeta(1000000,2,7)
Y1 = rbeta(1000000,7,2)
hist(X1, freq=FALSE, breaks=100, col="lightblue", main="X1")
hist(Y1, freq=FALSE, breaks=100, col="lightblue", main="Y1")
S_2a = X1 + Y1
hist(S_2a, freq=FALSE, breaks=100, col="lightblue", main="S_2a = X1 + Y1")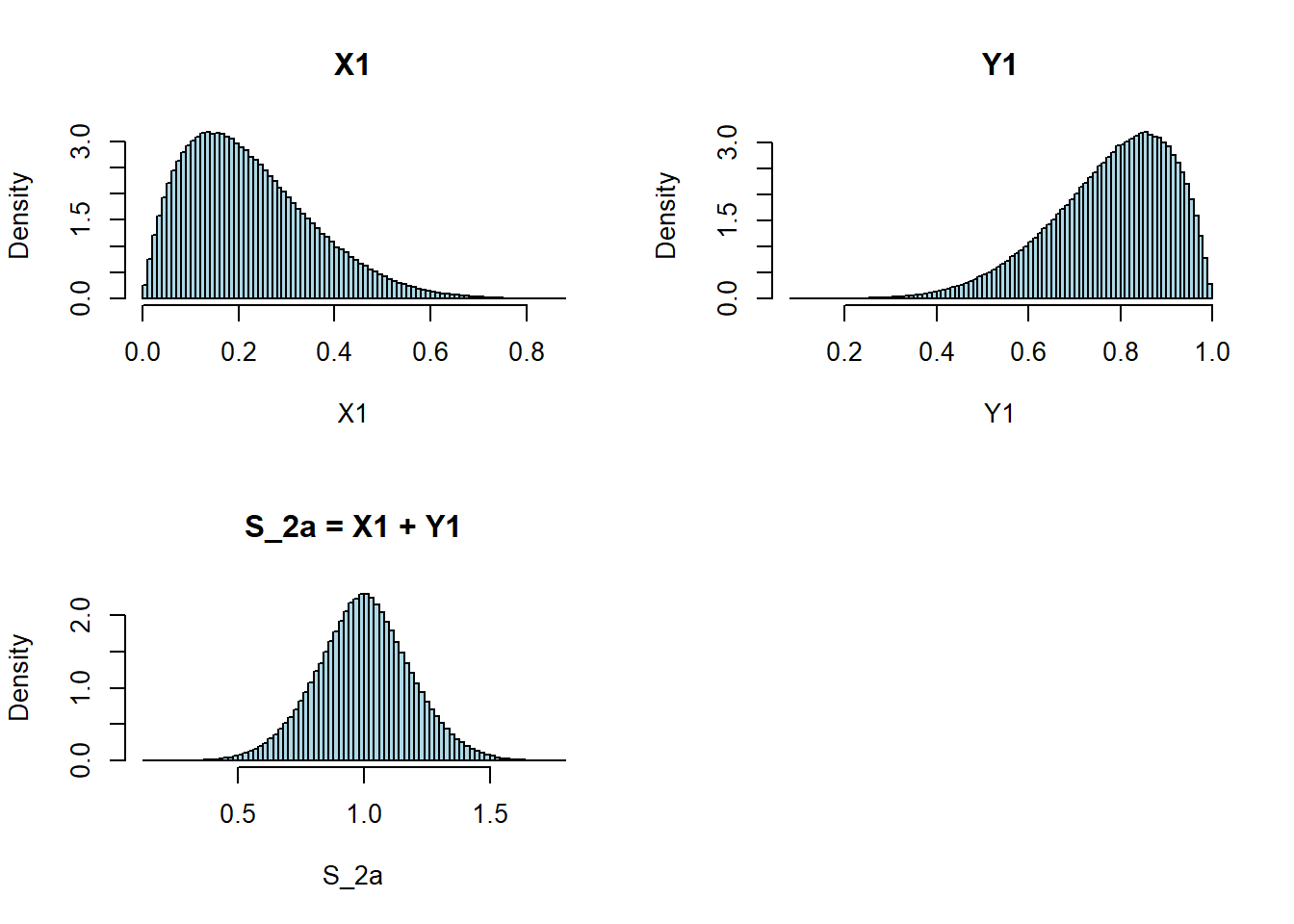
- \(S_{2b} = X_1 + Y_1\), onde \(n + m = 2\)
- \(X_i \sim Beta(\alpha = 2, \beta = 5)\)
- \(Y_j \sim Beta(\alpha = 2, \beta = 5)\)
par(mfrow=c(2,2))
X1 = rbeta(1000000,2,5)
Y1 = rbeta(1000000,2,5)
hist(X1, freq=FALSE, breaks=100, col="lightblue", main="X1")
hist(Y1, freq=FALSE, breaks=100, col="lightblue", main="Y1")
S_2b = X1 + Y1
hist(S_2b, freq=FALSE, breaks=100, col="lightblue", main=expression(paste("Distribuição de ",S[2~b],"=",X[1]+Y[1])))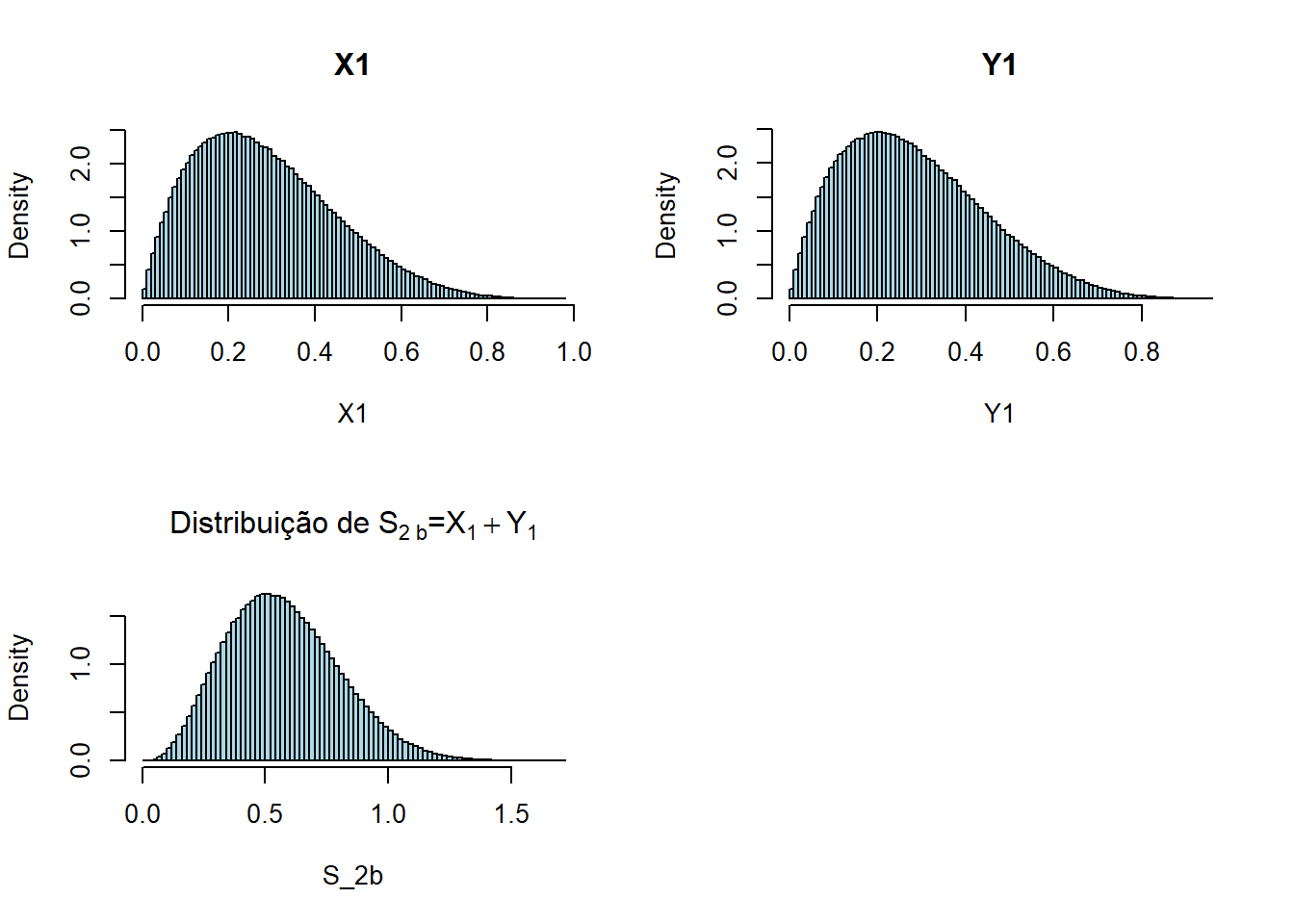
A soma de 10 variáveis aleatórias assimétricas \(X_i \sim Beta(2,5)\) resulta em uma distribuição normal, ou aproximadamente normal. Observe o resultado da simulação abaixo.
par(mfrow=c(2,2))
X_i = matrix(rbeta(10000000,2,5), 1000000,10)
hist(X_i[,1], freq=FALSE, breaks=100, col="lightblue", main="X1")
S = apply(X_i,1,sum)
hist(S, freq=FALSE, breaks=100, col="lightblue", main="S = X1 + ... + X10")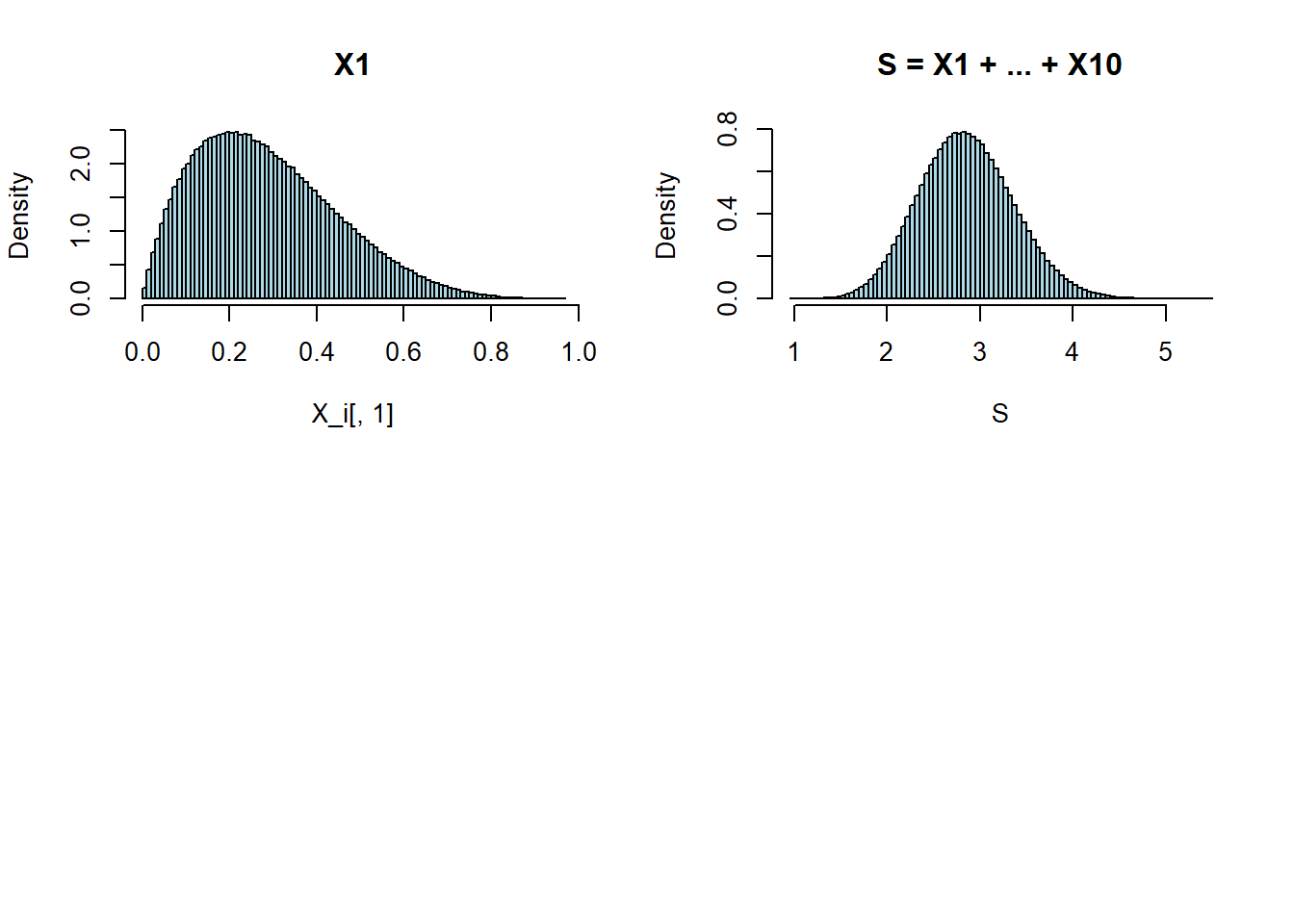
Diferença de variáveis aleatórias
O mesmo procedimento adotado
par(mfrow=c(2,2))
X1 = rnorm(1000000,5,2)
Y1 = runif(1000000,2,12)
hist(X1, freq=FALSE, breaks=100, col="lightblue", main="X1")
hist(Y1, freq=FALSE, breaks=100, col="lightblue", main="Y1")
D_2 = X1 - Y1
hist(D_2, freq=FALSE, breaks=100, col="lightblue", main=expression(paste("Distribuição de ",D[2],"=",X[1]-Y[1])))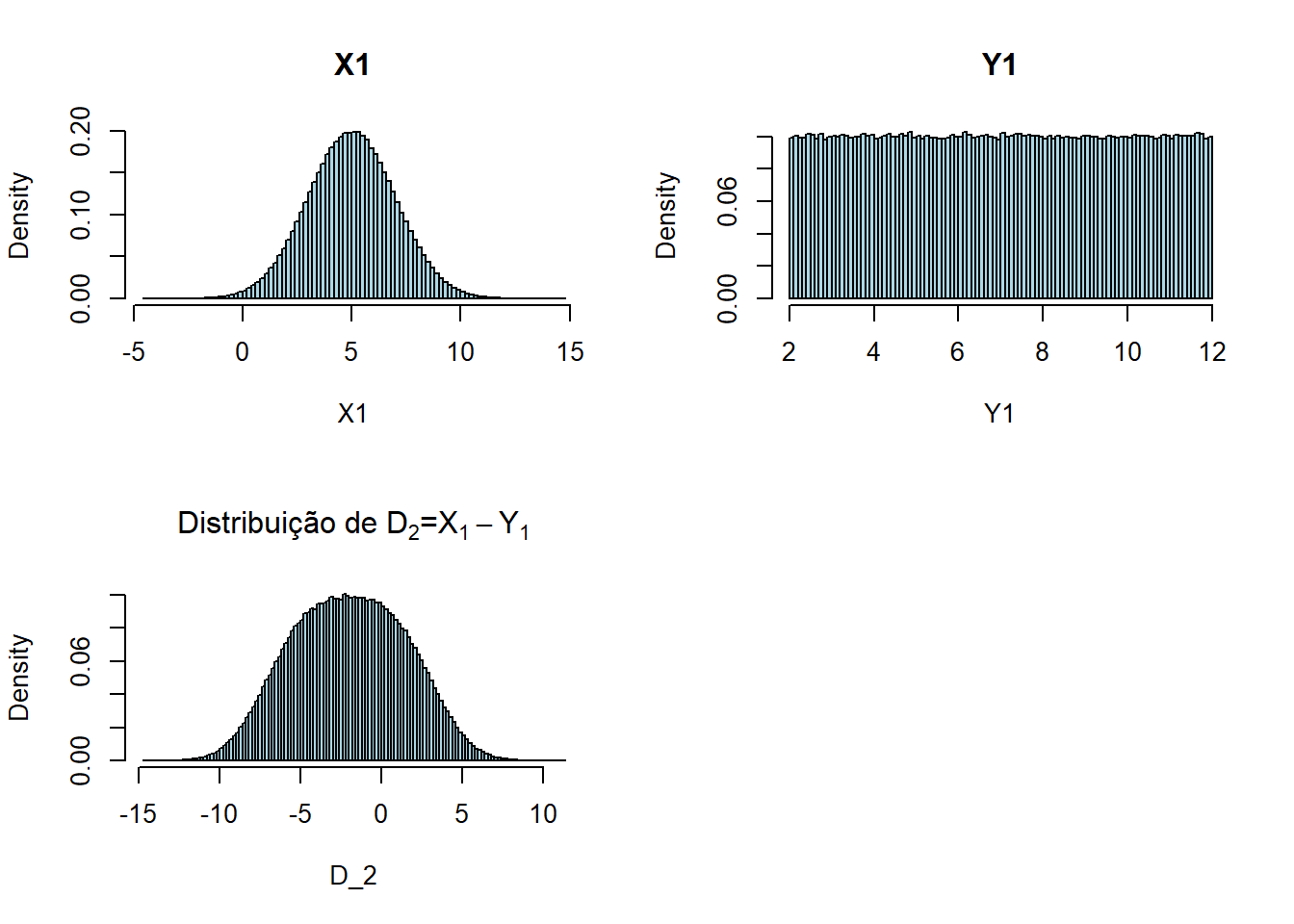
par(mfrow=c(3,2))
X1 = rnorm(1000000,5,2)
X2 = rnorm(1000000,5,2)
Y1 = runif(1000000,2,12)
Y2 = runif(1000000,2,12)
hist(X1, freq=FALSE, breaks=100, col="blue", main="X1")
hist(X2, freq=FALSE, breaks=100, col="blue", main="X2")
hist(Y1, freq=FALSE, breaks=100, col="blue", main="Y1")
hist(Y2, freq=FALSE, breaks=100, col="blue", main="Y2")
D_4 = X1 - X2 - Y1 - Y2
hist(D_4, freq=FALSE, breaks=100, col="blue", main=expression(paste("Distribuição de ",D[4],"=",X[1]-X[2]-Y[1]-Y[2])))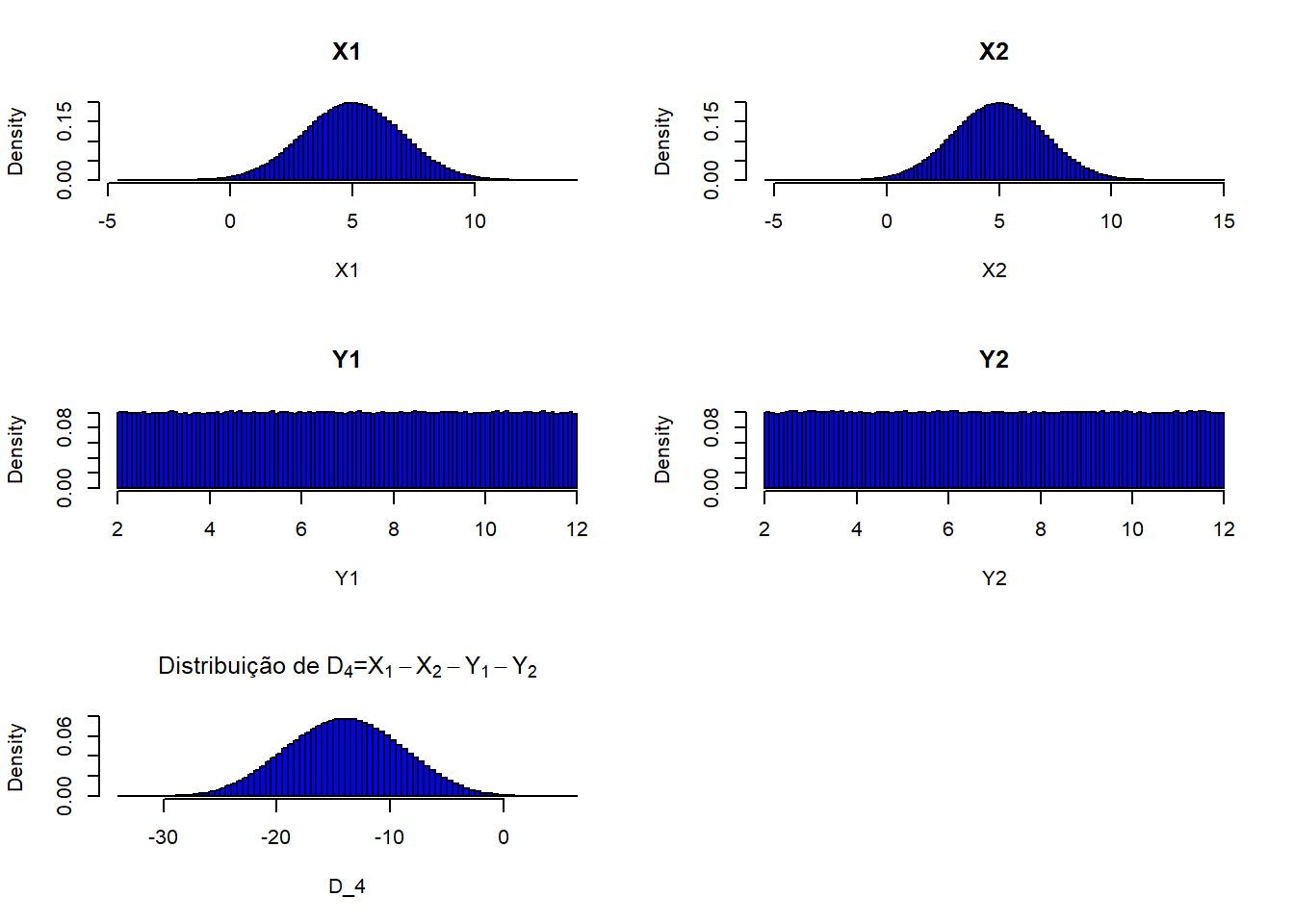
Funções de variáveis aleatórias
- \(F = 2X_1\)
- \(S = X_1 + X_2\)
- \(X_i \sim N(\mu = 4, \sigma^2 = 3^2)\)
par(mfrow=c(2,2))
X1 = rnorm(1000000,4,3)
X2 = rnorm(1000000,4,3)
hist(X1, freq=FALSE, breaks=100, col="lightblue", main="X1")
S = X1 + X2
F = 2*X1
hist(S, freq=FALSE, breaks=100, col="lightblue", main=expression(paste("Distribuição de S =",X[1]+X[2])))
hist(F, freq=FALSE, breaks=100, col="lightblue", main=expression(paste("Distribuição de F =",2~X[1])))
#
cat("E[X1] = ", mean(X1), "\nV(X1) = ", var(X1))E[X1] = 3.998486
V(X1) = 9.02424cat("\nE[X2] = ", mean(X2), "\nV(X2) = ", var(X2))
E[X2] = 3.998761
V(X2) = 9.014726cat("E[S] = ", mean(S), "\nV(S) = ", var(S))E[S] = 7.997247
V(S) = 18.05191cat("\nE[F] = ", mean(F), "\nV(F) = ", var(F))
E[F] = 7.996973
V(F) = 36.09696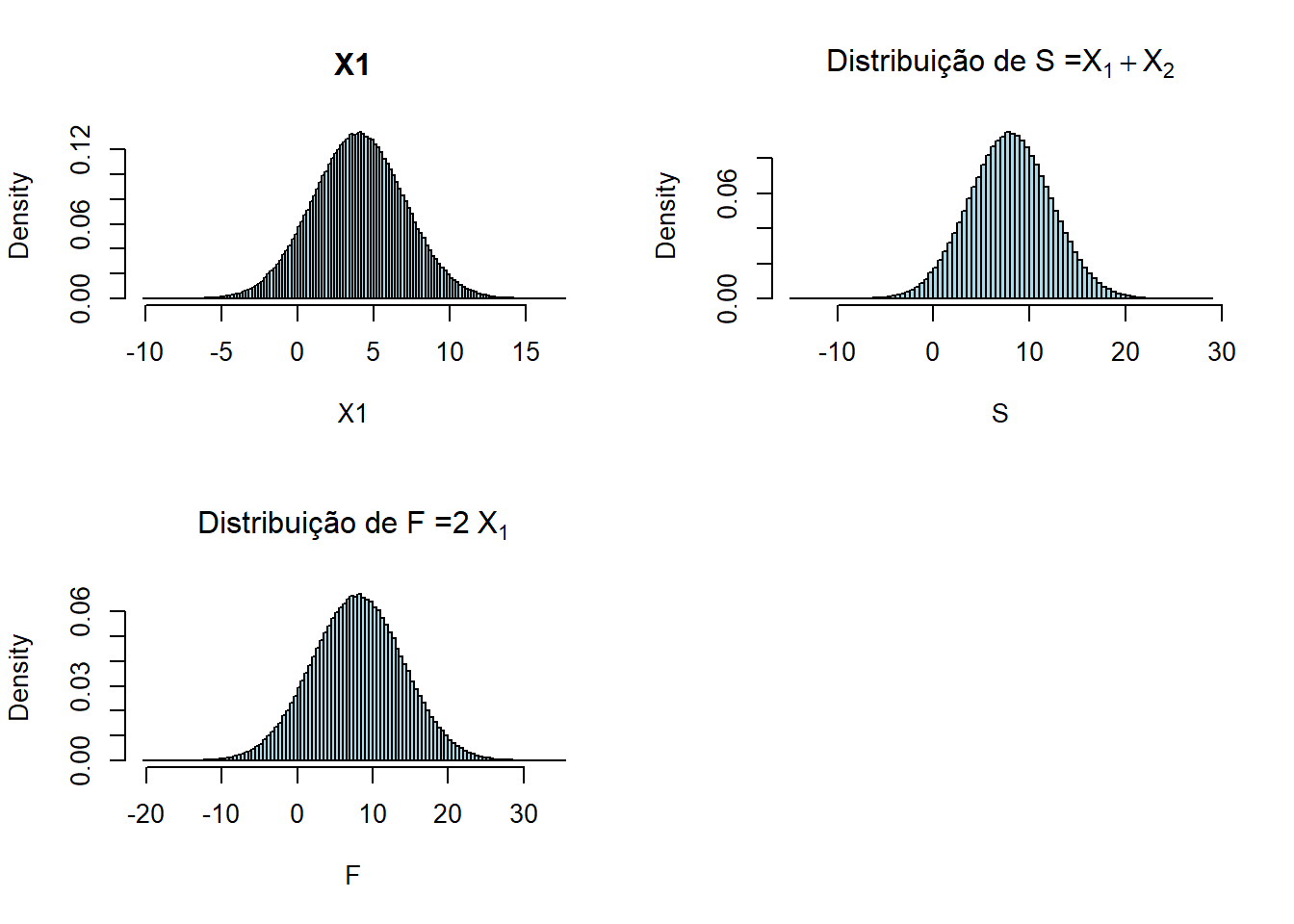
Propriedadaes calculadas pelas regras:
- \(E[S] = E[X1] + X[X2] = 4 + 4 = 8\)
- \(V[S] = V(X_1) + V(X_2) = 9 + 9 = 18\)
- \(E[F] = 2E[X1] = 2*4 = 8\)
- \(V[F] = 2^2V(X_1) = 4*9 = 36\)
Note que a função \(F = 2X_1\) assume dependência entre as variáveis aleatórias, \(F = X_1 + X_1\), dessa forma podemos calcular utilizando a regra para v.a.s dependentes:
- \(Cov(X,X) = V(X)\)
- \(V[F] = V(X_1) + V(X_1) + 2Cov(X_1,X_1) = 9 + 9 + 2*9 = 36\)
Exemplo - Distribuição Amostral e Soma/Diferença de v.a.s - 1
Uma empresa importadora de telas de computador tem a seu cargo a embalagem e distribuição dessas mesmas telas. Está atualmente em estudo um tipo de embalagem para um novo modelo a ser comercializado sendo a característica mais crítica a espessura (ou profundidade) de cada unidade depois de embalada.
Cada unidade vem do fabricante numa caixa cuja espessura total (já com uma unidade no seu interior) é variável e segue uma distribuição Normal com média 135 mm e desvio padrão 6 mm, isto é, \(N(\mu=135, \sigma^2=6^2)\). Antes de enviar as unidades para os seus clientes a empresa distribuidora tem de envolver a caixa de cada unidade com um revestimento resistente ao choque. Este revestimento consiste numa folha de um material protetor que é utilizada para envolver a embalagem inicial. Cada folha tem uma determinada espessura que se pode considerar constante em toda a superfície. No entanto a espessura das folhas varia de folha para folha de acordo com uma distribuição uniforme com os seguintes parâmetros \(U(14mm, 16mm)\).
- Qual a probabilidade da espessura de uma unidade, antes de ser revestida com uma folha do material protetor, ser superior a 140 mm? Indique claramente todos os cálculos necessários.
- Qual o valor esperado e a variância da espessura total da embalagem de uma unidade depois de envolvida por uma folha de material protetor? Note que uma folha do revestimento cobre todas as faces da embalagem inicial. Justifique o seu raciocínio.
- Para enviar ao cliente final as unidades revestidas são colocadas num caixa cujo comprimento é variável de acordo com uma distribuição Normal com as seguintes características \(N(\mu=2500, \sigma^2=10^2)\). Qual a probabilidade de a espessura total de 15 unidades revestidas com uma folha do material protector ser superior ao comprimento de uma caixa escolhida ao acaso? Indique todos os cálculos necessários e justifique todos os pressupostos associados à resolução do problema.
Solução
A v.a. espessura (E) segue uma distribuição Normal, \(E \sim N(\mu = 135,\ sigma^2 = 6^2)\). A v.a. revestimento (R) segue uma distribuição Uniforme \(R \sim U(a = 14, b = 16)\)
- Qual a probabilidade da espessura de uma unidade, antes de ser revestida com uma folha do material protetor, ser superior a 140 mm? Indique claramente todos os cálculos necessários.
library(ggplot2)
media = 135
desvpad = 6
funcShaded <- function(x) {
y <- dnorm(x, mean = media, sd = desvpad)
y[ x < 140] = NA
return(y)
}
li = media - 4*desvpad
ls = media + 4*desvpad
ggplot(data.frame(x=c(li,ls)),aes(x=x)) +
stat_function(fun=dnorm,geom = "line",size=1,col="green",args = c(mean=media,sd=desvpad)) +
stat_function(fun=funcShaded, geom="area", fill="#84CA72", alpha=0.2) +
scale_x_continuous(name = "espessura",breaks = seq(li,ls,desvpad)) +
scale_y_continuous(name = expression(f[E](e)))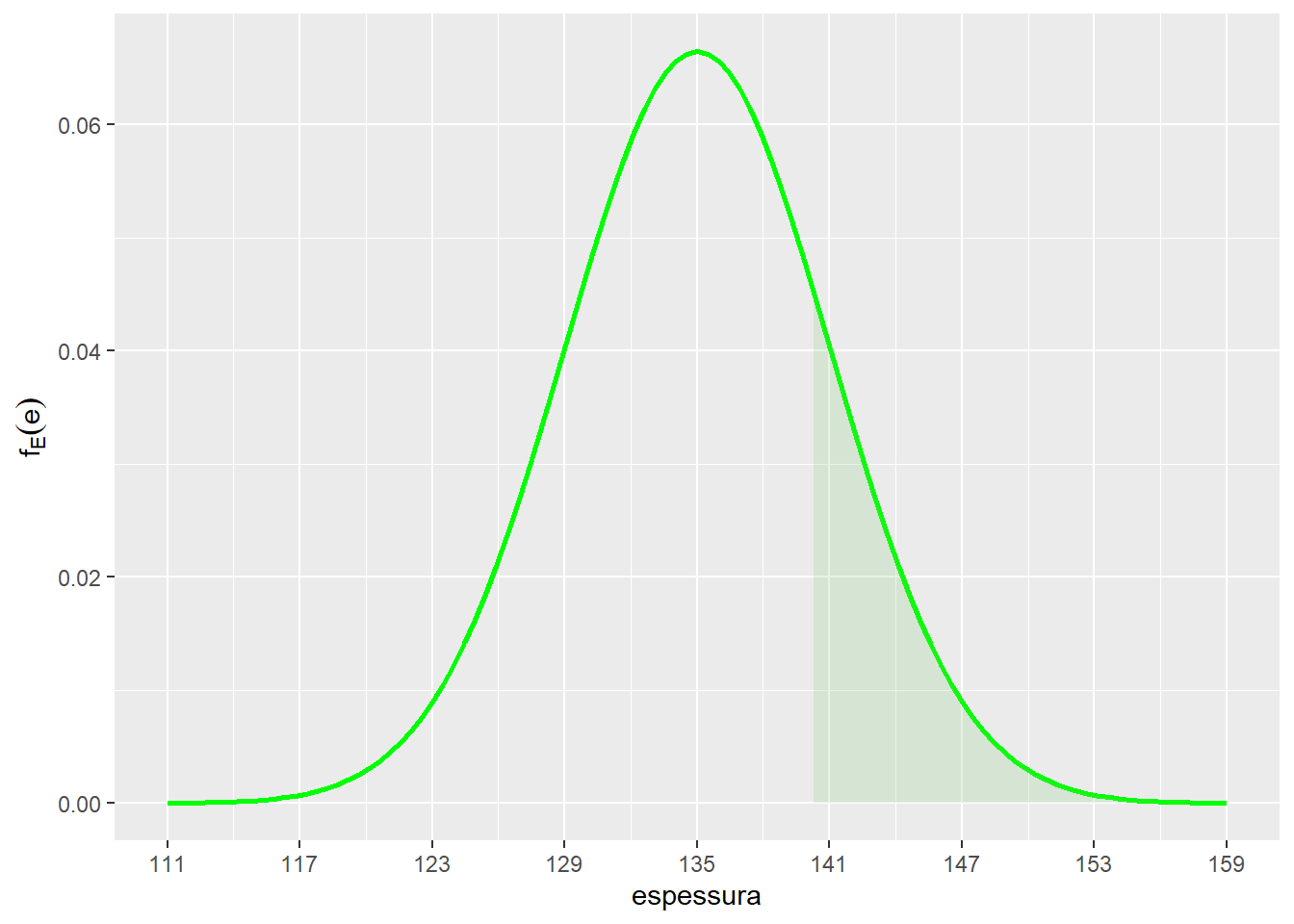
mu = 135 # média
sd = 6 # desvio padrão
# phi(x) = F(x) = função cumulativa normal
p = 1 - pnorm(140,mu,sd)
# utilizando cat como print de var e texto.
cat("P(E > 140) = ", p, "\n")P(E > 140) = 0.2023284 - Qual o valor esperado e a variância da espessura total da embalagem de uma unidade depois de envolvida por uma folha de material protetor? Note que uma folha do revestimento cobre todas as faces da embalagem inicial. Justifique o seu raciocínio.
A v.a. espessura total (T) é uma função de variáveis aleatórias da seginte forma:
A v.a. espessura (E) segue uma distribuição Normal, \(E \sim N(\mu = 135,\ sigma^2 = 6^2)\).
A v.a. revestimento (R) segue uma distribuição Uniforme \(R \sim U(a = 14, b = 16)\)
\[ T = E + 2R \] Note que a função (\(T\)) de v.a.s é também uma v.a. com uma distribuição de probabilidade/densidade. Note que a espessura total considera a espessura da caixa (E) mais duas vezes a espessura do revestimento (R), pois é exatamente mesma v.a. sendo considerada duas vezes, uma vez para cada lado. Caso o revestimento fosse consirado diferentes laminas de papel estes seriam revestimentos independentes um do outro, dessa forma deveria ser considerado (\(R_1 + R_2\)).
Para essa função podemos demonstrar via simulação, aquilo que já previamente sabemos, que éssa v.a. possui distribuição normal (dado pelo Teorema Central do Limite). Como demonstração note a simulação abaixo:
# E - normal
media = 135
desvpad = 6
# U - Uniforme
a = 14
b = 16
E = rnorm(1000000, media,desvpad)
R = runif(1000000,a,b)
par(mfrow=c(3,1))
hist(E, freq=FALSE, breaks=100, col="lightblue", main="E")
hist(R, freq=FALSE, breaks=100, col="lightblue", main="R")
T = E + 2*R
hist(T, freq=FALSE, breaks=100, col="lightblue", main="T = E + 2R")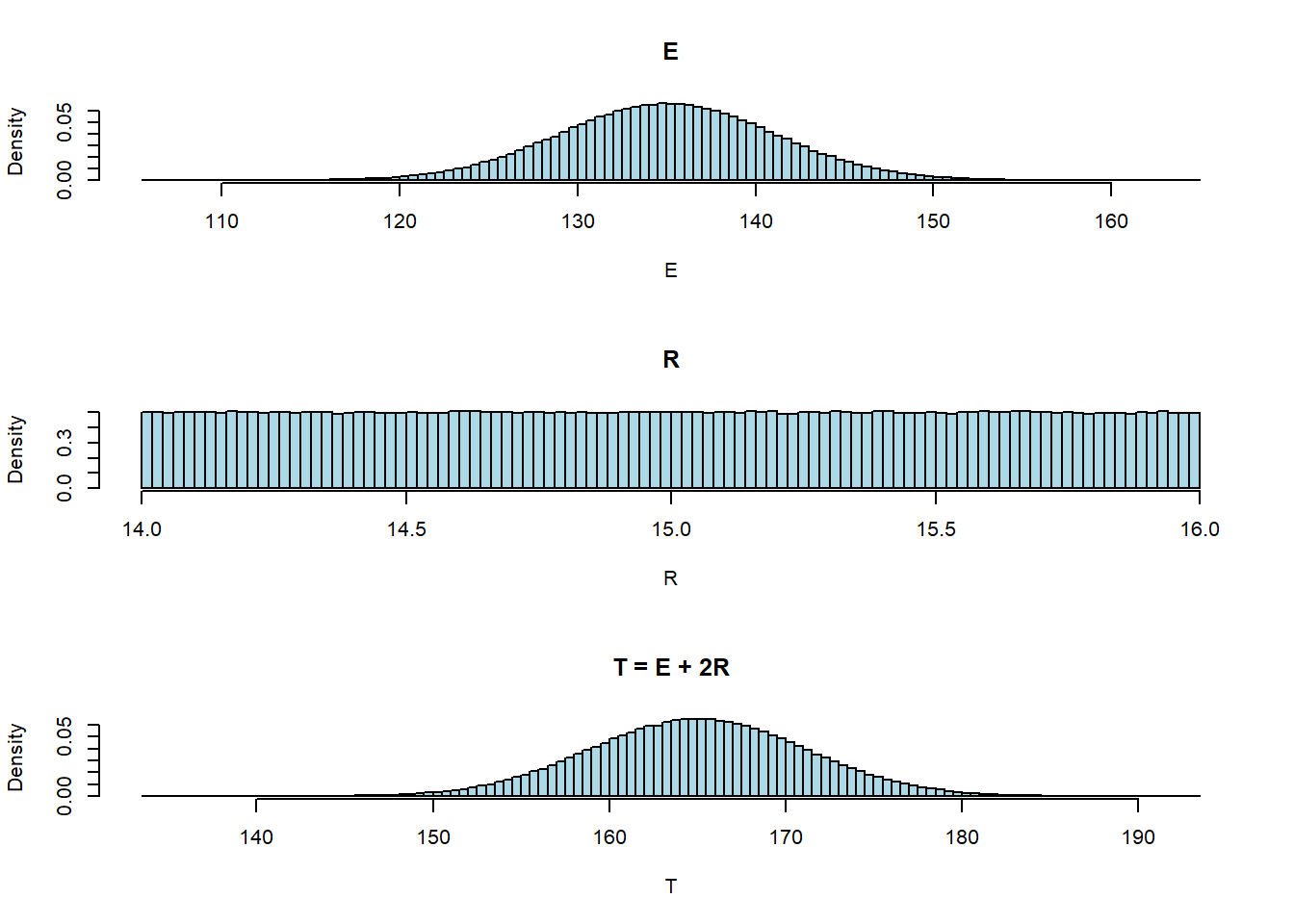
#
cat("E[T] = ", mean(T), "\nV(T) = ", var(T))E[T] = 165.0129
V(T) = 37.31636\[E[T] = E[E] + 2E[R] = 135 + 2(15) = 165\]
\[V(T) = V(E) + 2^2V(R) = 36 + 4(0.333) = 37.333\]
- Para enviar ao cliente final as unidades revestidas são colocadas num caixa cujo comprimento é variável de acordo com uma distribuição Normal com as seguintes características \(N(\mu=2500, \sigma^2=10^2)\).
Qual a probabilidade de a espessura total de 15 unidades revestidas com uma folha do material protetor ser superior ao comprimento de uma caixa escolhida ao acaso? Indique todos os cálculos necessários e justifique todos os pressupostos associados à resolução do problema.
A v.a. caixa (C) segue uma distribuição Normal \(C \sim N(\mu = 2500,\ sigma^2 = 10^2)\).
Vamos calcular a variável aleatória que se refere às 15 unidades de embalagens. Cada embalagem segue uma \(T \sim N(\mu = 165,\ sigma^2 = 37.333)\).
Considere \(W = T_1 + ... + T_{15}\) que é a soma de 15 v.a.s \(T\) independentes. Dessa forma sabemas que a forma dessa distribuição segue uma Normal, com as seguintes propriedades:
\[E[W] = \sum_{i=1}^{15}{E[T_i]} = 2475\] \[V[W] = \sum_{i=1}^{15}{V(T_i)} = 560\]
Temos que \(W \sim N(\mu = 2475,\ sigma^2 = 560)\).
Agora vamos verificar todas as possíveis diferenças (\(D\)) entre as 15 embalagens (\(W\)) e uma caixa (\(C\)) e calcular a probabilidade de \(P(D > 0)\).
Novamente, sabemos que a v.a. \(D\) que é a diferença, \(D = W - C\), segue uma distribuição normal, com as seguintes propriedades:
\[D = W - C \]
\[E[D] = E[W] - E[C] = 2475 - 2500 = -25\]
\[V(D) = V(W) + V(C) = 560 + 100 = 660\]
\[DP[D] = \sqrt{660} = 25.69\]
Ou seja a diferença entre as 15 embalagens e a caixa segue uma normal, \(W \sim N(\mu = -25,\ sigma^2 = 660)\). Onde \(P(D > 0)\) ocorre quando (\(W\)) possui comprimento superior ao da caixa (\(C\)).
library(ggplot2)
media = -25
desvpad = 25.69
funcShaded <- function(x) {
y <- dnorm(x, mean = media, sd = desvpad)
y[ x < 0] = NA
return(y)
}
li = media - 4*desvpad
ls = media + 4*desvpad
ggplot(data.frame(x=c(li,ls)),aes(x=x)) +
stat_function(fun=dnorm,geom = "line",size=1,col="black",args = c(mean=media,sd=desvpad)) +
stat_function(fun=funcShaded, geom="area", fill="orange", alpha=0.2) +
scale_x_continuous(name = "diferenças",breaks = seq(li,ls,desvpad)) +
scale_y_continuous(name = expression(f[D](d)))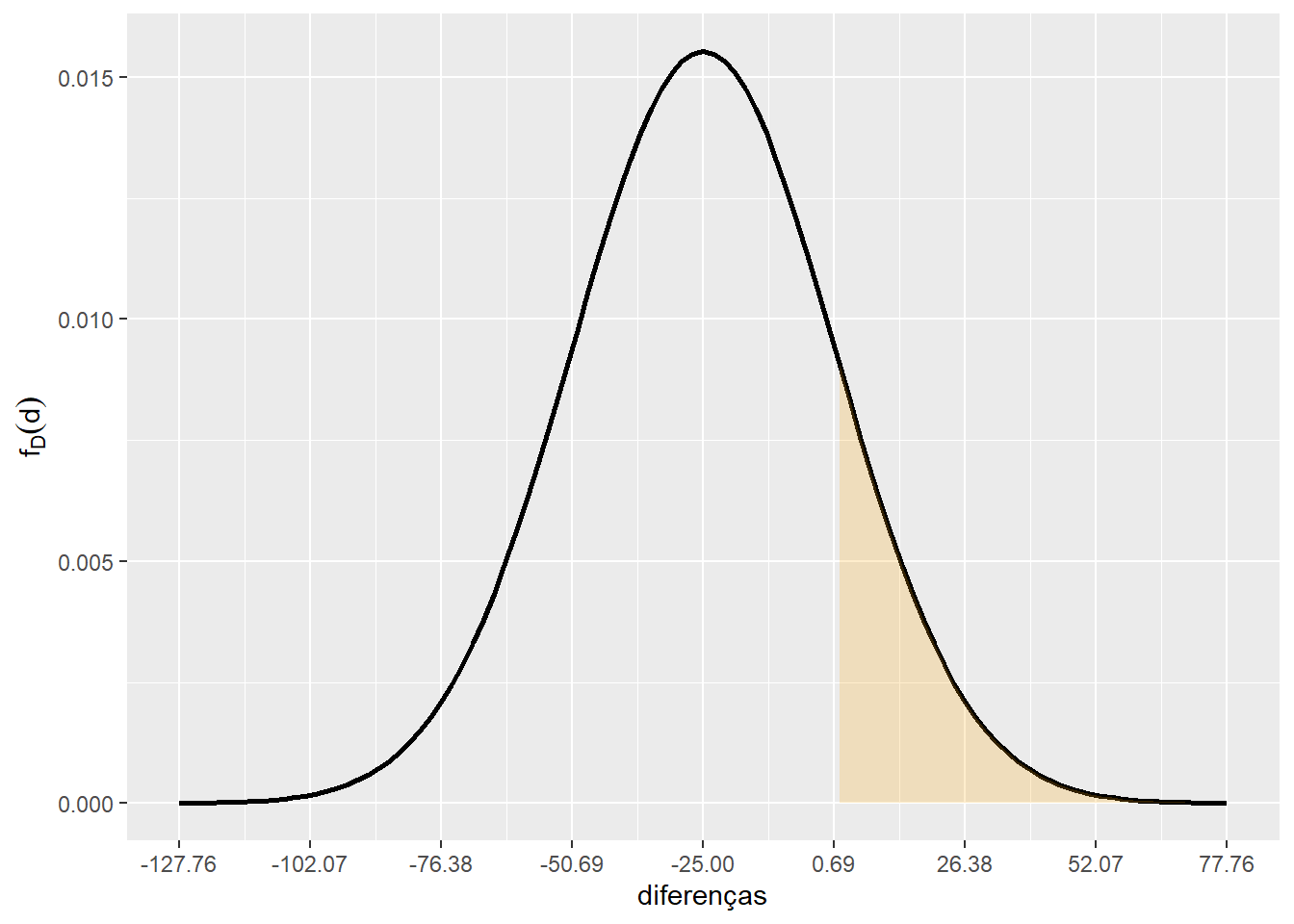
mu = -25 # média
sd = 25.69 # desvio padrão
# phi(x) = F(x) = função cumulativa normal
p = 1 - pnorm(0,mu,sd)
# utilizando cat como print de var e texto.
cat("P(D > 0) = ", p, "\n")P(D > 0) = 0.1652415 Exemplo - Distribuição Amostral e Soma/Diferença de v.a.s - 2
Um estudo recente revela que o tempo de reação dos condutores de automóvel segue uma distribuição Normal. Em particular, no caso dos condutores que obtiveram a carteira na Escola de condução AprendeRápido o tempo de reação apresenta uma média de 0.45 segundos e um desvio padrão de 0.3 segundos. Por outro lado o tempo médio de reação de um condutor da Escola CarteiraFácil é de 0.4 segundos. Sabe-se ainda que a probabilidade do tempo de reação de um condutor da Escola CarteiraFácil ser superior a 0.5 segundos é de 30.9%.
- Qual a probabilidade do tempo de reação de um condutor da Escola AprendeRápido ser superior 0.6 segundos?
- Determine o desvio padrão do tempo de reação de um condutor da Escola CarteiraFácil.
- Suponha agora que se pretende estudar o tempo de reação de uma amostra aleatória de 30 condutores com carteira de condução obtida pela Escola AprendeRápido e de 20 condutores com carteira obtida pela Escola CarteiraFácil.
- Se submetermos os condutores das duas escolas a um teste para aferir o seu tempo de reação, qual a probabilidade do total dos seus tempos de reação ser inferior a 25 segundos?
- Qual a probabilidade de a média dos tempos de reação dos condutores da Escola AprendeRápido seleccionados ser inferior à média dos tempos de reação dos condutores da Escola CarteiraFácil seleccionados?
Solução
AprendeRápido, \(A \sim N(\mu = 0.45, \sigma^2 = 0.3^2)\)
CarteiraFácil, \(C \sim N(\mu = 0.40, \sigma^2 = ?)\)
- Qual a probabilidade do tempo de reação de um condutor da Escola AprendeRápido ser superior 0.6 segundos?
\[ \mathbb{P}(A > 0.6) = \mathbb{P}(Z > \frac{0.6 - 0.45}{0.3}) = \mathbb{P}(Z > 0.5) = 0.3085375 \]
media = 0.45
desvpad = 0.3
1-pnorm(0.6,media,desvpad)[1] 0.3085375- Determine o desvio padrão do tempo de reação de um condutor da Escola CarteiraFácil.
\[ \sigma = ? \\ \mathbb{P}(C > 0.5) = 0.309\\ \frac{0.5 - 0.4}{\sigma} = 0.5 \\ \sigma = \frac{0.5 - 0.4}{0.5} = 0.2\\ \] Assim temos que, CarteiraFácil, \(C \sim N(\mu = 0.40, \sigma^2 = 0.2^2)\)
- Suponha agora que se pretende estudar o tempo de reação de uma amostra aleatória de 30 condutores com carteira de condução obtida pela Escola AprendeRápido e de 20 condutores com carteira obtida pela Escola CarteiraFácil.
\[ n_A = 30\\ n_B = 20\\ \] i) Se submetermos os condutores das duas escolas a um teste para aferir o seu tempo de reação, qual a probabilidade do total dos seus tempos de reação ser inferior a 25 segundos?
A distribuição dos condutores das duas autoescolas, considerando \(30\) da Escola AprendeRápido (A) e \(20\) da CarteiraFácil (C) segue uma distribuição normal.
\[ S = \sum_{i=1}^{30}{A_i} + \sum_{j=1}^{20}{C_j}\\ E[S] = \sum_{i=1}^{30}{E[A_i]} + \sum_{j=1}^{20}{E[C_j]} = 21.5\\ V(S) = \sum_{i=1}^{30}{V(A_i)} + \sum_{j=1}^{20}{V(C_j)} = 3.5 = 1.870829^2\\ \]
E_S = 30*0.45 + 20*0.40
V_S = 30*0.3^2 + 20*0.2^2
E_S[1] 21.5V_S[1] 3.5sqrt(V_S)[1] 1.870829Assim temos que \(S \sim N(\mu = 21.5, \sigma^2 = 1.870829^2)\), e a probabilidade de \(S\) ser inferior a 25 segundos é calculada por:
\[ \mathbb{P}(S < 25) = \mathbb{P}( Z < \frac{25 - 21.5}{1.870829}) = 0.96 \]
media = 21.5
desvpad = 1.870829
pnorm(25,media,desvpad)[1] 0.9693156library(ggplot2)
media = 21.5
desvpad = 1.870829
funcShaded <- function(x) {
y <- dnorm(x, mean = media, sd = desvpad)
y[ x > 25] = NA
return(y)
}
li = media - 4*desvpad
ls = media + 4*desvpad
ggplot(data.frame(x=c(li,ls)),aes(x=x)) +
stat_function(fun=dnorm,geom = "line",size=1,col="black",args = c(mean=media,sd=desvpad)) +
stat_function(fun=funcShaded, geom="area", fill="orange", alpha=0.2) +
scale_x_continuous(name = "S",breaks = seq(li,ls,desvpad)) +
scale_y_continuous(name = expression(f[S](s)))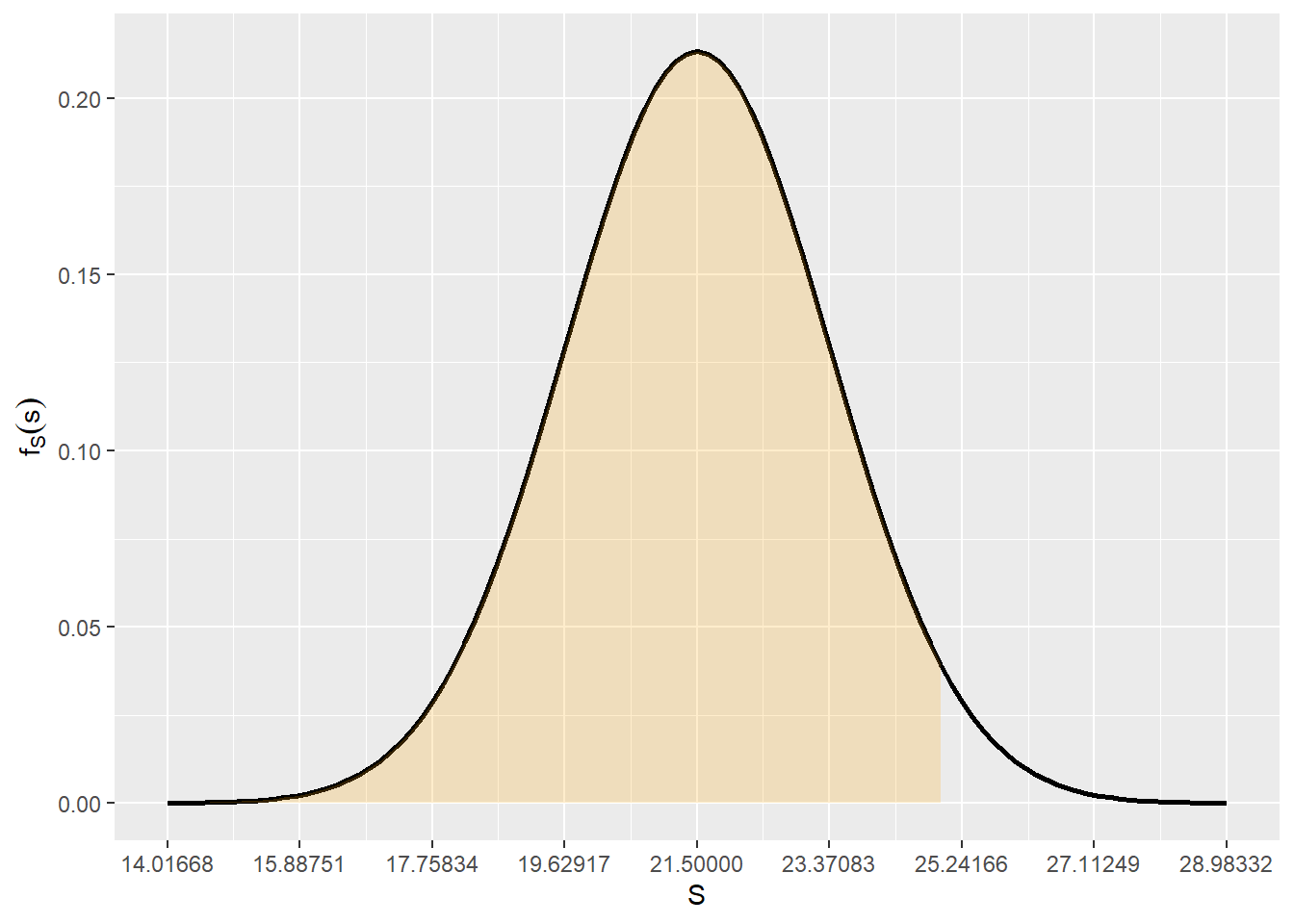 ii) Qual a probabilidade de a média dos tempos de reação dos condutores da Escola AprendeRápido seleccionados ser inferior à média dos tempos de reação dos condutores da Escola CarteiraFácil seleccionados?
ii) Qual a probabilidade de a média dos tempos de reação dos condutores da Escola AprendeRápido seleccionados ser inferior à média dos tempos de reação dos condutores da Escola CarteiraFácil seleccionados?
Calcularemos a distribuição das médias amostrais, para cada um dos casos.
\(\overline{A} \sim N(\mu_A,\sigma^2_A=\sigma^2/n)\)
\(\overline{C} \sim N(\mu_C,\sigma^2_C=\sigma^2/n)\)
\[ \begin{align} E[\overline{A}] &= 0.45\\ V(\overline{A}) &= \frac{\sigma^2_A}{n_A}=\frac{0.3^2}{30} = 0.055^2 \\ . \\ E[\overline{C}] &= 0.40\\ V(\overline{C}) &= \frac{\sigma^2_C}{n_B}=\frac{0.2^2}{20} = 0.045^2 \\ \end{align} \] Obtendo a distribuição da diferença entre as médias:
\[ \begin{align} D &= \overline{A} - \overline{C}\\ E[D] &= 0.45 - 0.40 = 0.05\\ V(D) &= 0.055^2 + 0.045^2 = 0.071^2\\ \end{align} \] A probabilidade da diferença ser menor que zero é dada por:
\[ \mathbb{P}(D < 0) = 0.2406 \]
media = 0.05
desvpad = 0.071
pnorm(0,media,desvpad)[1] 0.2406462library(ggplot2)
media = 0.05
desvpad = 0.071
funcShaded <- function(x) {
y <- dnorm(x, mean = media, sd = desvpad)
y[ x > 0] = NA
return(y)
}
li = media - 4*desvpad
ls = media + 4*desvpad
ggplot(data.frame(x=c(li,ls)),aes(x=x)) +
stat_function(fun=dnorm,geom = "line",size=1,col="black",args = c(mean=media,sd=desvpad)) +
stat_function(fun=funcShaded, geom="area", fill="orange", alpha=0.2) +
scale_x_continuous(name = "S",breaks = seq(li,ls,desvpad)) +
scale_y_continuous(name = expression(f[S](s)))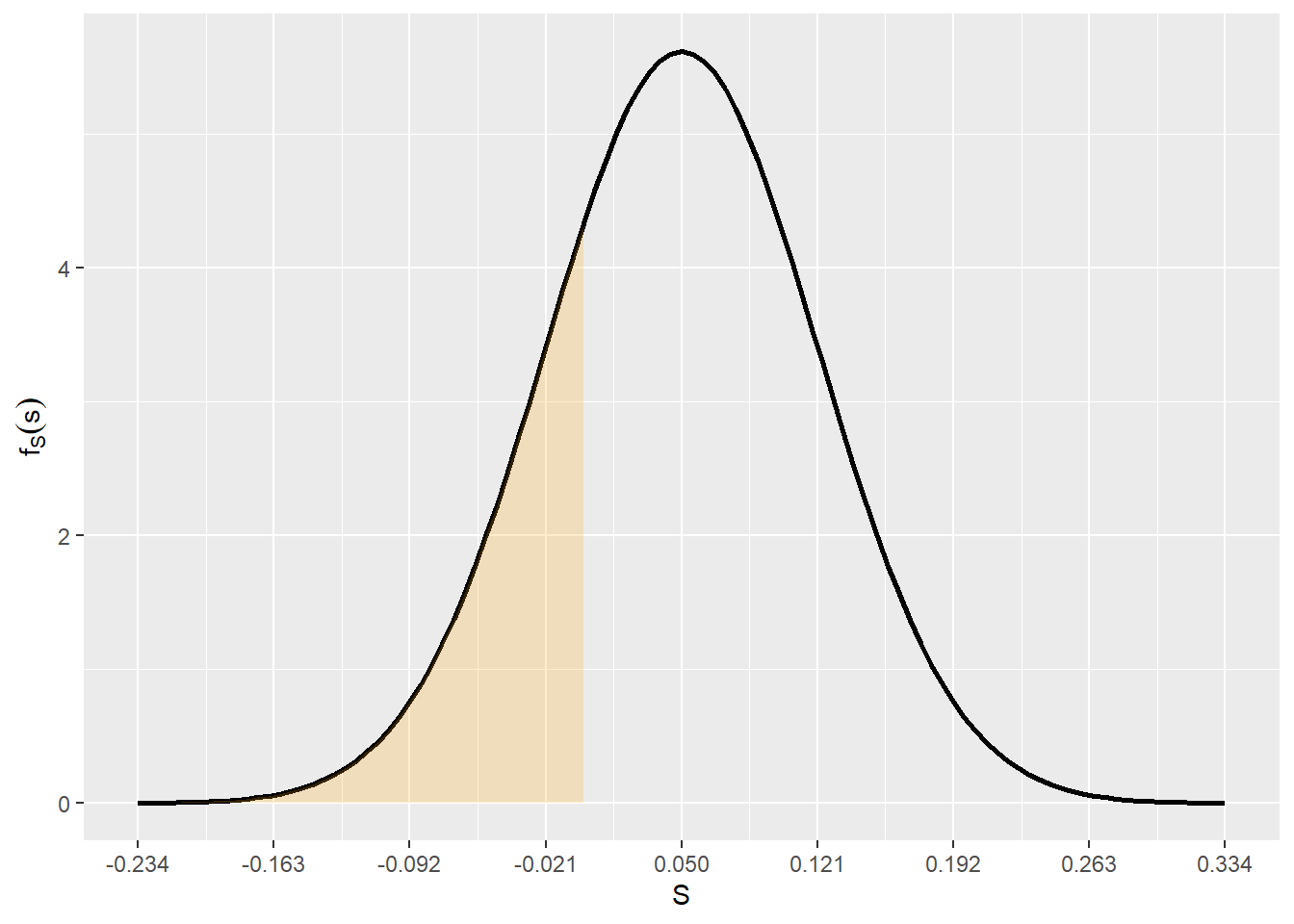
Exemplo - Distribuição Amostral e Soma/Diferença de v.a.s - 3
Uma fábrica tem uma máquina para ensacar cimento Portland automaticamente, sendo o peso médio dos sacos igual a \(\mu\) = 50.0 kg com um desvio padrão de \(\sigma\) = 1.6 kg. Para evitar reclamações, o fabricante dá uma indenização de R$ 5,00 por cada saco fornecido com menos de 48.0 kg. Sabe-se que o peso dos sacos segue uma distribuição normal.
- Qual o valor esperado da indenização no caso de serem fornecidos 200 sacos de cimento?
- Devido ao sucesso de vendas o fabricante decidiu comprar uma nova máquina, onde o peso dos sacos também segue uma distribuição normal com um desvio padrão de \(\sigma\) = 1.6 kg. Para quanto se deve regular o peso médio dos sacos da nova máquina para que o custo esperado de indenização de 200 sacos caia para R$ 40,00?
- Admita que o peso médio da nova máquina é de \(\mu\) = 51.0 kg, e o desvio padrão de \(\sigma\) = 1.6 kg. Qual a probabilidade do peso médio de 15 sacos escolhidos ao acaso da máquina antiga ser superior ao peso médio de 20 sacos escolhidos ao acaso da máquina nova?
Solução
Seja a variável aleatória \(X_A\) peso dos sacos de cimento, \(X_A \sim (\mu = 50.0,\sigma^2=1.6^2)\).
- Qual o valor esperado da indenização no caso de serem fornecidos 200 sacos de cimento?
A probabilidade de um saco de cimento ter peso inferior à 48 kg é:
\[ \mathbb{P}(X_A < 48) = 0.1056 \]
media = 50
desvpad = 1.6
pnorm(48,media,desvpad)[1] 0.1056498O valor esperado da indenização será:
\[ 200 \cdot 5 \cdot 0.1056 = 105.6 \]
- Devido ao sucesso de vendas o fabricante decidiu comprar uma nova máquina, onde o peso dos sacos também segue uma distribuição normal com um desvio padrão de \(\sigma\) = 1.6 kg. Para quanto se deve regular o peso médio dos sacos da nova máquina para que o custo esperado de indenização de 200 sacos caia para R$ 40,00?
\[ \begin{align} 200 \cdot 5 \cdot \mathbb{P}(X_N < 48) &= 40\\ \mathbb{P}(X_N < 48) &= 0.04\\ \mathbb{P}(Z < \frac{48 - x}{1.6}) &= 0.04\\ .\\ z &= \frac{48 - x}{1.6}\\ .\\ -1.75 &= \frac{48 - x}{1.6}\\ x &= 50.8\\ \mu &= 50.8 \space kg \end{align} \]
- Admita que o peso médio da nova máquina é de \(\mu\) = 51.0 kg, e o desvio padrão de \(\sigma\) = 1.6 kg. Qual a probabilidade do peso médio de 15 sacos escolhidos ao acaso da máquina antiga ser superior ao peso médio de 20 sacos escolhidos ao acaso da máquina nova?
Seja a variável aleatória \(X_{nova} \sim N(\mu = 51.0,\sigma^2 = 1.6^2)\), e dessa foi retirada uma amostra de \(n_{nova} = 20\) sacos onde a distribuição da média amostral segue uma normal (teoremas..) e as propriedades são:
\[ \begin{align} E[\overline{X}_{nova}] &= 51.0\\ V(\overline{X}_{nova}) &= \frac{\sigma^2}{n_{nova}}=\frac{1.6^2}{20} = 0.3577^2\\ . \\ E[\overline{X}_{antiga}] &= 50.0\\ V(\overline{X}_{antiga}) &= \frac{\sigma^2}{n_{antiga}}=\frac{1.6^2}{15} = 0.4131^2\\ \end{align} \] Temos que a diferença das duas distribuições é dada por:
\[ \begin{align} D &= \overline{X}_{antiga} - \overline{X}_{nova}\\ E[D] &= 50 - 51.0 = -1\\ V(D) &= 0.4131^2 + 0.3577^2 = 0.54644^2\\ \end{align} \]
\[ \mathbb{P}(D > 0) = 0.03362 \]
media = -1
desvpad = 0.54644
1 - pnorm(0,media,desvpad)[1] 0.03362294library(ggplot2)
media = -1
desvpad = 0.54644
funcShaded <- function(x) {
y <- dnorm(x, mean = media, sd = desvpad)
y[ x < 0] = NA
return(y)
}
li = media - 4*desvpad
ls = media + 4*desvpad
ggplot(data.frame(x=c(li,ls)),aes(x=x)) +
stat_function(fun=dnorm,geom = "line",size=1,col="black",args = c(mean=media,sd=desvpad)) +
stat_function(fun=funcShaded, geom="area", fill="orange", alpha=0.2) +
scale_x_continuous(name = "D",breaks = seq(li,ls,desvpad)) +
scale_y_continuous(name = expression(f[D](d)))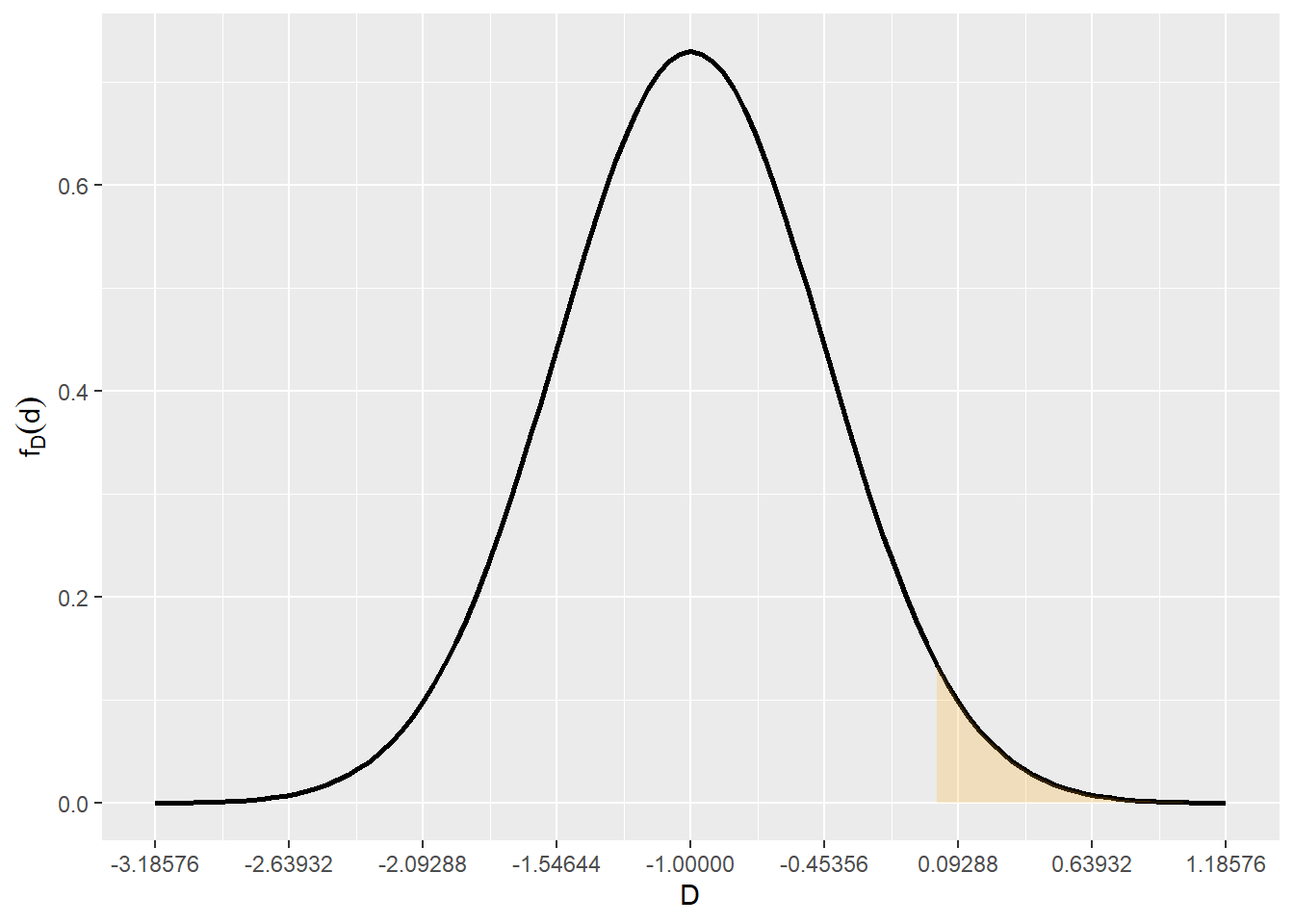
Exemplo - Distribuição Amostral e Soma/Diferença de v.a.s - 4
A loja Renner (Filial Florianópolis) fez um estudo sobre a quantidade gasta pelos seus clientes em cada visita à loja, tendo verificado que o montante gasto (em reais) por visita à loja segue uma distribuição aproximadamente normal, com média 100 e variância 324.
- Determine a percentagem de visitantes da loja que gasta menos de 80.
- Considere os clientes da loja que numa visita gastam entre 95 e 115. Estes clientes são denominados pela gerência como os clientes regulares.
- Calcule o valor esperado e variância do número de clientes regulares entre os próximos 30 visitantes da loja.
- Qual a probabilidade de entre os próximos 5 clientes estarem 3 clientes regulares?
- Num novo estudo constatou-se haver uma diferença significativa no que diz respeito à despesa de clientes femininos e masculinos. De fato, o montante gasto pelos clientes femininos segue uma distribuição Normal, \(F \sim (\mu = 70, \sigma = 14\)) e o montante gasto pelos clientes masculinos uma distribuição Normal \(M \sim (\mu = 65, \sigma = 16\)).
Solução
Seja a v.a. \(R \sim N(\mu=100,\sigma^2 =324)\).
- Determine a percentagem de visitantes da loja que gasta menos de 80.
\[ \mathbb{P}(R < 80) = 0.133 \]
media = 100
desvpad = 18
pnorm(80,media,desvpad)[1] 0.1332603- Considere os clientes da loja que numa visita gastam entre 95 e 115. Estes clientes são denominados pela gerência como os clientes regulares.
A probabilidade dos clientes serem regulares é:
\[ \mathbb{P}(95 < R < 115) = 0.407 \]
media = 100
desvpad = 18
pnorm(115,media,desvpad) - pnorm(95,media,desvpad)[1] 0.4070801- Calcule o valor esperado e variância do número de clientes regulares entre os próximos 30 visitantes da loja.
O número de clientes regulares (sucesso) entre os próximos 30 visitantes (tentativas) é uma v.a. binomial.
\(X \sim Bin(n = 30, p = 0.407)\)
\[ \begin{align} E[X] &= np = 30 \cdot 0.407 = 12.21\\ V(X) &= np(1-p)= 30 \cdot 0.407(1-0.407)=7.241 \end{align} \]
- Qual a probabilidade de entre os próximos 5 clientes estarem 3 clientes regulares?
\(X \sim Bin(n = 5, p = 0.407)\)
\[ p_X(3) = \mathbb{P}(X=3)=\left(\begin{array}{c}5\\3\end{array}\right) 0.407^3(1-0.407)^{5-3}=0.237 \]
Num novo estudo constatou-se haver uma diferença significativa no que diz respeito à despesa de clientes femininos e masculinos. De fato, o montante gasto pelos clientes femininos segue uma distribuição Normal, \(F \sim (\mu = 70, \sigma = 14\)) e o montante gasto pelos clientes masculinos uma distribuição Normal \(M \sim (\mu = 65, \sigma = 16\)).
O gerente da loja Renner (Filial Florianópolis) foi informado que vai receber um grupo de clientes composto por 6 clientes femininos e 8 masculinos. Defina a variável gasto total desse grupo de clientes e determine a probabilidade destes em conjunto gastarem um montante igual ou superior a 1000 reais?
\[ \begin{align} T &= \sum_{i=1}^6{F_i} + \sum_{i=1}^8{M_i}\\ E[T] &= \sum_{i=1}^6{E[F_i]} + \sum_{i=1}^8{E[M_i]} = 940\\ V(T) &= \sum_{i=1}^6{V(F_i)} + \sum_{i=1}^8{V(M_i)} = 3224 = 56.78^2\\ \end{align} \]
A probabilidade do gasto total ser maior que 1000,
\[ \mathbb{P}(T > 1000) =0.1453 \]
media = 940
desvpad = 56.78
1 - pnorm(1000,media,desvpad)[1] 0.145322library(ggplot2)
media = 940
desvpad = 56.78
funcShaded <- function(x) {
y <- dnorm(x, mean = media, sd = desvpad)
y[ x < 1000] = NA
return(y)
}
li = media - 4*desvpad
ls = media + 4*desvpad
ggplot(data.frame(x=c(li,ls)),aes(x=x)) +
stat_function(fun=dnorm,geom = "line",size=1,col="black",args = c(mean=media,sd=desvpad)) +
stat_function(fun=funcShaded, geom="area", fill="orange", alpha=0.2) +
scale_x_continuous(name = "T",breaks = seq(li,ls,desvpad)) +
scale_y_continuous(name = expression(f[T](t)))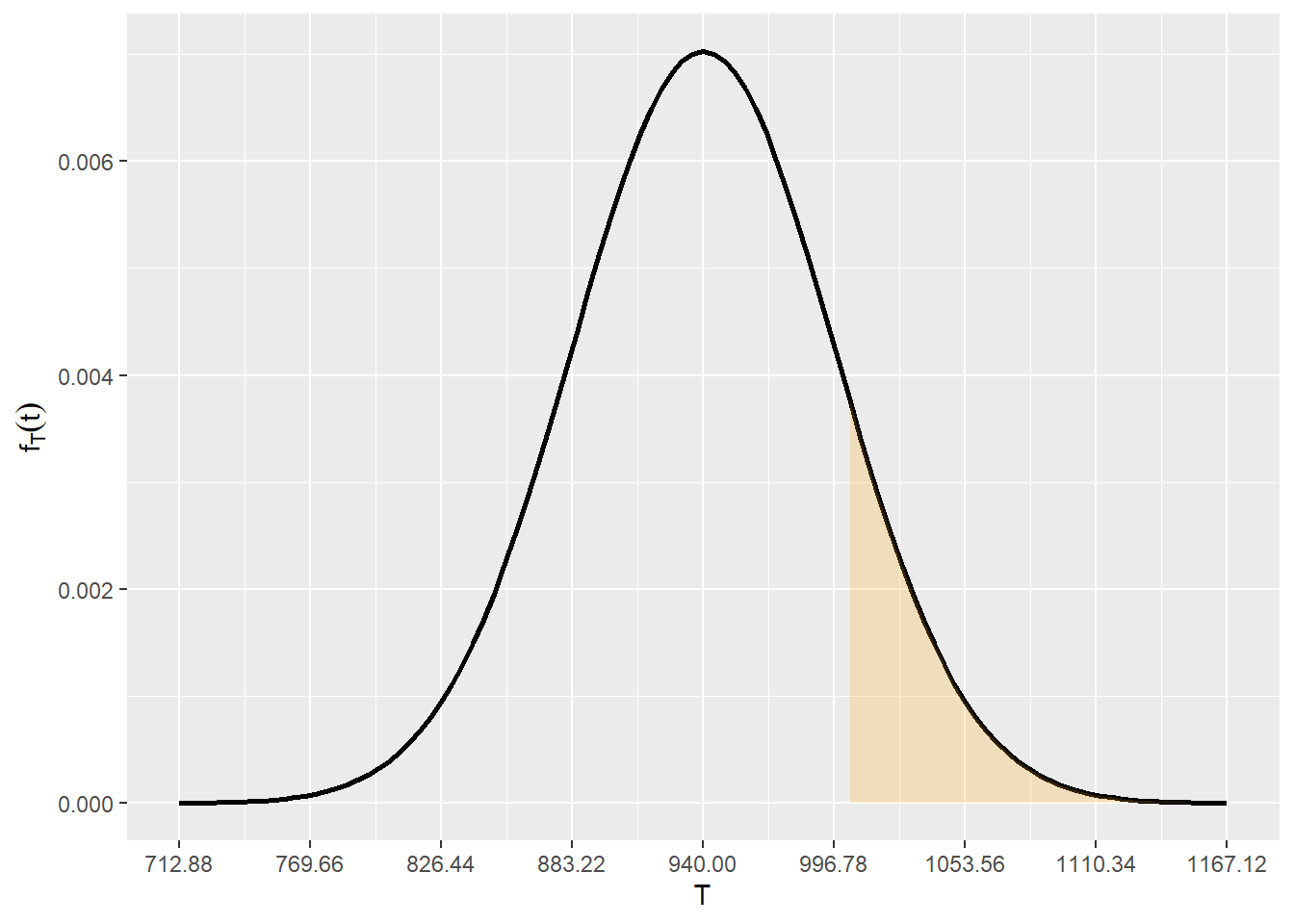
Exemplo - Distribuição Amostral e Soma/Diferença de v.a.s - 5
Uma máquina de enchimento de bolas de basquete está sob avaliação do engenheiro da fábrica. O engenheiro quer saber se é necessário comprar uma nova máquina, então resolveu fazer algumas análises.
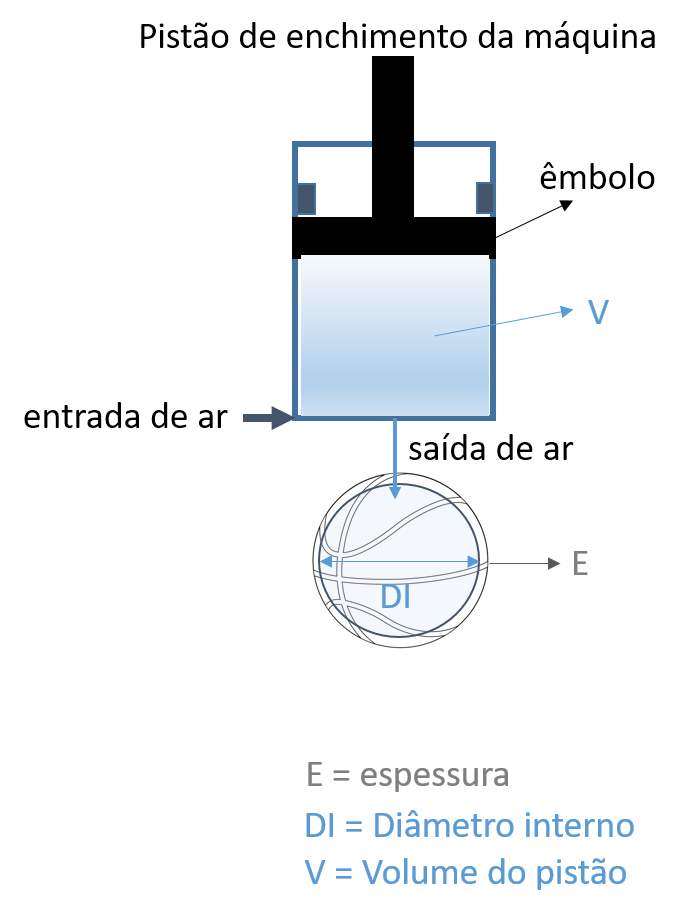
A máquina funciona deslocando o êmbolo para cima e para baixo. Quando o embolo sobe ele carrega o volume interno do pistão com ar, e quando o êmbolo desce o volume de ar é inserido dentro da bola, preenchendo o volume interno da bola fazendo com que o seu diâmetro interno aumente. Sabe-se que o volume interno do pistão (V) é uma variável aleatória com distribuição Uniforme \(V \sim U(8809, 9579)\) \(cm^3\). As subidas e descidas do êmbolo são independentes. Sabe-se também que a espessura (E) das bolas segue uma distribuição Normal de valor esperado 1.0 cm e desvio padrão 0.05 cm, independente do diâmetro interno.
A atual máquina sob avaliação necessita de oito volumes (V) \(cm^3\) para encher totalmente o volume (VT) \(cm^3\) de uma bola de basquete. O diâmetro interno da bola totalmente cheia (DI) é uma função do volume total (VT) de enchimento da bola, dado pela equação abaixo.
\[ DI = 0.0002.VT + 36.52 \]
- Determine qual é a forma de distribuição das variáveis aleatórias VT, DI e Diâmetro Externo, calcule os valores esperados e variâncias. Represente graficamente. Indique os pressupostos da sua resposta.
- Uma bola é considerada com defeito sempre que o seu diâmetro externo exceder 53.56 cm. Calcule a probabilidade de uma bola ser defeituosa.
- Considere que um lote contém 9 bolas que são posteriormente colocadas em caixas quadradas (3 x 3 bolas) para o envio para clientes. O comprimento do lado de cada caixa segue uma distribuição Normal com valor esperado 160.0 cm e desvio padrão 1.0 cm.
- O cliente rejeita o lote se este apresentar 2 ou mais bolas defeituosas. Calcule a probabilidade do cliente rejeitar um lote. Justifique o raciocínio.
- Qual a probabilidade do comprimento total de 3 bolas ser superior ao comprimento do lado de uma caixa escolhida ao acaso? Indique todos os cálculos necessários e pressupostos associados à resolução do problema.
Solução
- Determine qual é a forma de distribuição das variáveis aleatórias VT, DI e Diâmetro Externo, calcule os valores esperados e variâncias. Represente graficamente. Indique os pressupostos da sua resposta.
O volume total (VT) é a soma de oito volumes do pistão, sendo equivalente a:
\[ VT = \sum_{i=1}^{8}V \]
O volume (\(V \sim U(8809, 9579)\)) é uma v.a uniforme com os seguintes parâmetros:
\[ \begin{align} E[V] &= \frac{b+a}{2} = \frac{(8809 + 9579)}{2} = 9194\\ V(V) &= \frac{(b-a)^2}{12} = \frac{(9579 - 8809)^2}{12} = 49408.33\\ \end{align} \] A soma de oito v.a.s uniformes levam (se aproxima) à uma distribuição normal. Os parâmetros dessa distribuição normal podem ser calculados utilizando a propriedade da linearidade do valor esperado.
\[ \begin{align} VT &= \sum_{i=1}^8{V}\\ E[VT] &= \sum_{i=1}^8{E[V]} = \sum_{i=1}^8{(9194)} = 73552 \\ V(VT) &= \sum_{i=1}^8{(49408.33)} = 395266.6\\ \end{align} \]
Assim temos que \(VT\) é uma v.a com distribuição normal, \(VT \sim N(\mu = 73552, \sigma^2 = 395266.6)\).
O diâmetro interno da bola totalmente cheia (DI) é uma função do volume total (VT) de enchimento da bola, dado pela equação abaixo. Tal função é linear sendo a v.a. \(VT\) normal, consequentemente \(DI\) é uma v.a com distribuição normal \(DI \sim N(\mu = 51.23 , \sigma^2 = 0.0158)\).
\[ \begin{align} DI &= 0.0002.VT + 36.52\\ E[DI] &= 0.0002.E[VT] + 36.52 = 0.0002 \cdot (73552) + 36.52 = 51.23 \\ V(DI) &= 0.0002^2.V(VT) + 0 = 0.0002^2 \cdot (395266.6) = 0.0158 \\ \end{align} \]
O diâmetro externo (\(DE\)) da bola é função do diâmetro interno (\(DI\)) e da espessura (\(E\)), sendo ambas \(DI\) e \(E\) normais, sua soma também é normal, ou seja \(DE \sim N(\mu = 53.23 , \sigma^2 = 0.0258)\):
\[ \begin{align} DE &= DI + 2 \cdot E\\ E[DE] &= E[DI] + 2 \cdot E[E] = 51.23 + 2 \cdot (1.0) = 53.23 \\ V(DE) &= V(DI) + 2^2 \cdot V(E) = 0.0158 + 2^2 \cdot (0.05^2) = 0.0258 \\ \end{align} \]
Pressupostos assumidos: - Volumes (V) são independentes e identicamente distribuidos
- Uma bola é considerada com defeito sempre que o seu diâmetro externo exceder 53.56 cm. Calcule a probabilidade de uma bola ser defeituosa.
Devemos calcular a proabilidade de o diâmetro externo (DE) exceder 53.56 cm.
\[ DI \sim N(\mu = 53.23 , \sigma^2 = 0.0258)\\ \mathbb{P}(DE > 53.56) = \]
media = 53.23
desvpad = 0.1606238
1 - pnorm(53.56,media,desvpad)[1] 0.01996414library(ggplot2)
media = 53.23
desvpad = 0.1606238
funcShaded <- function(x) {
y <- dnorm(x, mean = media, sd = desvpad)
y[ x < 53.56] = NA
return(y)
}
li = media - 4*desvpad
ls = media + 4*desvpad
ggplot(data.frame(x=c(li,ls)),aes(x=x)) +
stat_function(fun=dnorm,geom = "line",size=1,col="black",args = c(mean=media,sd=desvpad)) +
stat_function(fun=funcShaded, geom="area", fill="orange", alpha=0.2) +
scale_x_continuous(name = "DE",breaks = seq(li,ls,desvpad)) +
scale_y_continuous(name = expression(f[DE](de)))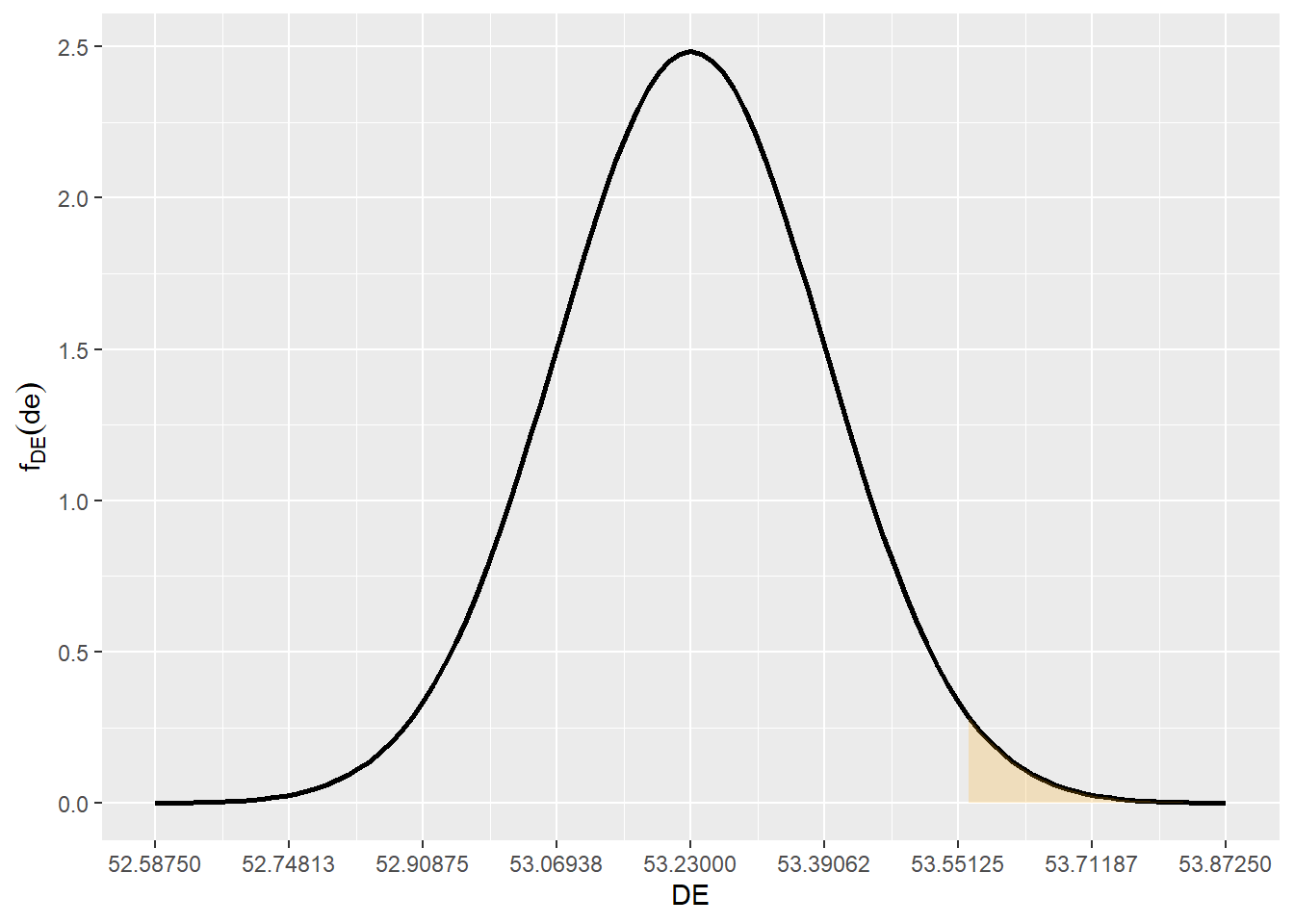
Considere que um lote contém 9 bolas que são posteriormente colocadas em caixas quadradas (3 x 3 bolas) para o envio para clientes. O comprimento do lado de cada caixa segue uma distribuição Normal com valor esperado 160.0 cm e desvio padrão 1.0 cm.
O cliente rejeita o lote se este apresentar 2 ou mais bolas defeituosas. Calcule a probabilidade do cliente rejeitar um lote. Justifique o raciocínio.
Para esse caso temos que um lote com n = 9 bolas de basquete, onde queremos calcular a probabilidade de 2 ou mais serem defeituosas. Se X = “número de bolas defeituosas em 9 bolas” temos uma v.a binomial.
\[ \mathbb{P}(X \ge 2) = 1 - [\mathbb{P}(X = 0) + \mathbb{P}(X = 1)]\\ n = 9\\ p = 0.01996414\\ \mathbb{P}(X = 0) = \left(\begin{array}{c}9\\0\end{array}\right)0.01996^0 \cdot (1-0.01996)^9 = 0.8340541\\ \mathbb{P}(X = 0) = \left(\begin{array}{c}9\\1\end{array}\right)0.01996^1 \cdot (1-0.01996)^8 = 0.152881\\ \mathbb{P}(X \ge 2) = 0.0130649 \]
- Qual a probabilidade do comprimento total de 3 bolas ser superior ao comprimento do lado de uma caixa escolhida ao acaso? Indique todos os cálculos necessários e pressupostos associados à resolução do problema.
Aqui devemos verificar se as 3 bolas que possuem diametro externo dada pela normal pode exceder o comprimento da caixa.
Primeiro calcularemos a dimensão total (\(D_{Total}\)) das 3 bolas, que é a soma dos diâmetros externos (que é uma soma de v.a.s normais, que resulta em uma nova v.a normal) e deduziremos do comprimento total (\(C_{Total}\)), resultando na v.a referente a diferença entre as dimenões (\(Dif\)):
\[ D_{Total} = \sum_{i=1}^{3}DE\\ E[D_{Total}] = 159.69\\ V(D_{Total}) = 0.0774\\ .\\ Dif = C_{Total} - D_{Total}\\ E[Dif] = 160.0 - 159.69 = -0.308\\ V(Dif) = 1 + 0.0774 = 1.077\\ \]
A probabilidade do comprimento total de 3 bolas ser superior ao comprimento do lado de uma caixa escolhida ao acaso ocorrerá quando a \(Dif\) for superior a zero, neste caso temos:
\[ \mathbb{P}(Dif > 0) = 0.3833 \]
media = -0.308
desvpad = sqrt(1.077)
1 - pnorm(0,media,desvpad)[1] 0.3833151library(ggplot2)
media = -0.308
desvpad = sqrt(1.077)
funcShaded <- function(x) {
y <- dnorm(x, mean = media, sd = desvpad)
y[ x < 0] = NA
return(y)
}
li = media - 4*desvpad
ls = media + 4*desvpad
ggplot(data.frame(x=c(li,ls)),aes(x=x)) +
stat_function(fun=dnorm,geom = "line",size=1,col="black",args = c(mean=media,sd=desvpad)) +
stat_function(fun=funcShaded, geom="area", fill="orange", alpha=0.2) +
scale_x_continuous(name = "Dif",breaks = seq(li,ls,desvpad)) +
scale_y_continuous(name = expression(f[Dif](dif)))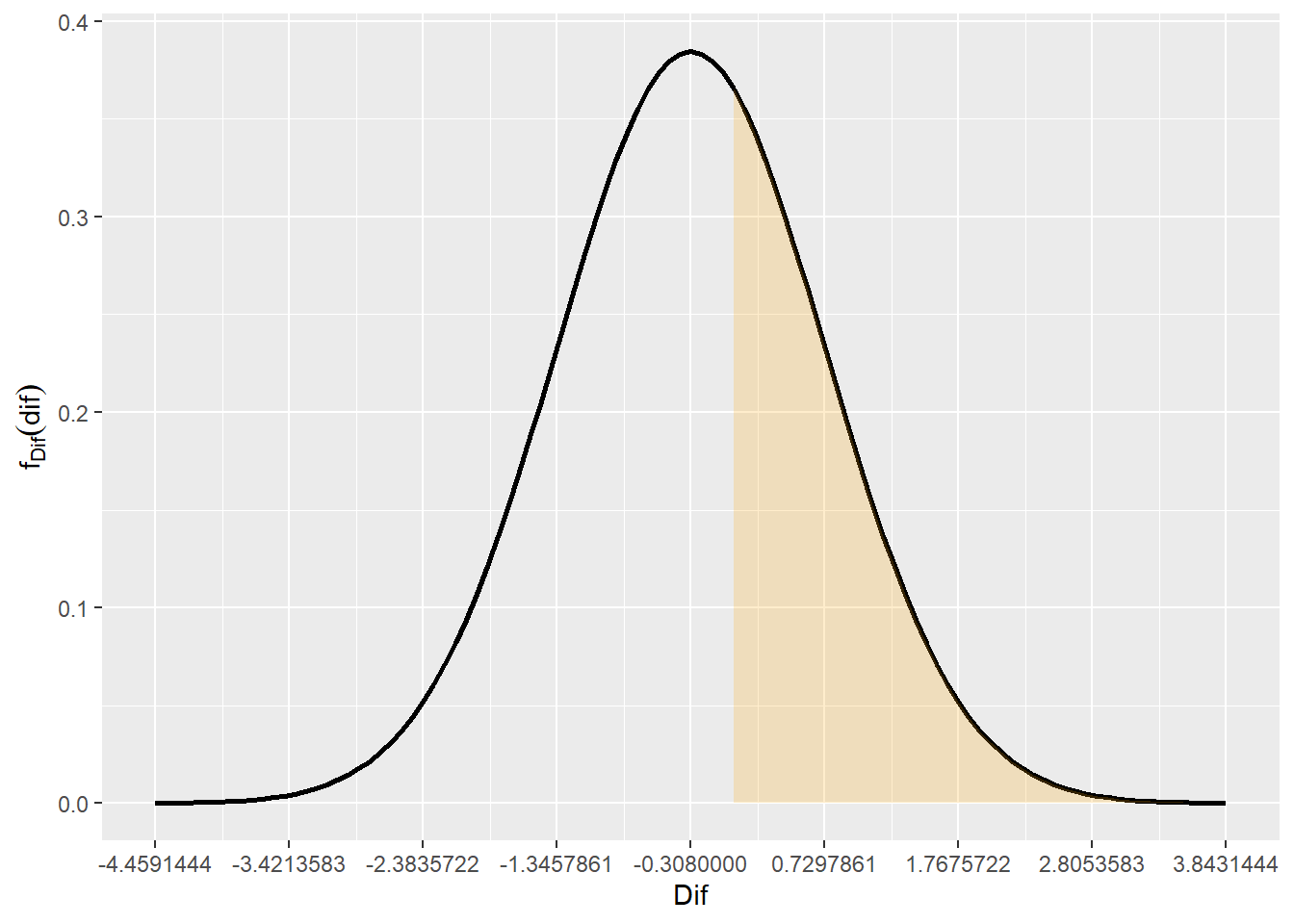
Este conteúdo está disponível por meio da Licença Creative Commons 4.0
