Distribuição do tempo de espera
As distribuições do tempo de espera é outra importante classe de problemas associados com a quantidade de tempo que leva para a ocorrência de um evento específico de interesse. Dentro dessa classe de problemas se enquadram duas distribuições bastante conhecidas, são elas:
Distribuição Geométrica
Nessa classe de problemas associados ao tempo de espera imagine o exemplo onde nós podemos lançar uma moeda, repetidamente, até que seja observado uma “cara”, ou ainda, podemos lançar uma bola de basquete na cesta repetidamente até acertarmos. A partir desse experimento temos interesse em calcular algumas probabilidades.
Dessa forma suponha que iremos conduzir repetidos experimentos de Bernoulli, observando as falhas e sucessos. Seja \(X\) o número de falhas antes do sucesso. Se \(P(Sucesso)=p\) então \(X\) possui a seguinte PMF,
Podemos dizer que \(X\) possui uma distribuição geométrica e escrever \(X \sim Geo(p)\).
Fica claro que \(p_X(x) \ge 0\) e que podemos verificar que \(\sum{p_X(x)}=1\)
\[ \sum\limits_{x=0}^{\infty}{p(1-p)^x}=p\sum\limits_{x=0}^{\infty}{(1-p)^x}=p\frac{1}{1-(1-p)}=1 \] resultado oriundo da série geométrica,
\[ \sum\limits_{k=0}^{\infty}{x^k}=\frac{1}{1-x}=1 \quad |x|< 1 \]
A variável aleatória geométrica é a única distribuição discreta com a propriedade de falta de memória que implica que se o experimento for iniciado em qualquer tentativa, não irá alterar a sua distribuição de probabilidades, ou seja a avaliação das probabilidades se iniciarem após algumas tentativas a distribuição não será afetada.
Exemplo - Geométrica 1
A probabilidade de um alinhamento ótico bem sucedido na montagem de produto de armazenamento de dados é de 0.80. Assuma que as tentativas são independentes.
- Qual é a probabilidade de que o primeiro alinhamento bem sucedido requeira exatamente quatro tentativas ?
- Qual é a probabilidade de que o primeiro alinhamento bem sucedido requeira no máximo quatro tentativas ?
- Qual é a probabilidade de que o primeiro alinhamento bem sucedido requeira ao menos quatro tentativas ?
Solução
- Qual é a probabilidade de que o primeiro alinhamento bem sucedido requeira exatamente quatro tentativas ?
Seja \(X\) o número de tentativas até a obtenção do primeiro alinhamento bem sucedido, temos uma variável aleatória com \(p = 0.8\).
Assim, temos que,
\[
\mathbb{P}(X = 3) = p_X(x)=0.8(1-0.8)^3 = 0.0064
\] Note que no R na função dgeom(x,p) \(x\) representa o número de fracassos, sendo neste caso \(x = 4 - 1 = 3\).
x = 3
p = 0.8
p_x = dgeom(x,p)
p_x[1] 0.0064- Qual é a probabilidade de que o primeiro alinhamento bem sucedido requeira no máximo quatro tentativas ?
\[ \mathbb{P}(X \le 3) = \mathbb{P}(X = 0) + \mathbb{P}(X = 1) + \mathbb{P}(X = 2) + \mathbb{P}(X = 3) = 0.9984 \]
x = seq(0,3,1)
p = 0.8
p_x = dgeom(x,p)
p_x[1] 0.8000 0.1600 0.0320 0.0064sum(p_x)[1] 0.9984- Qual é a probabilidade de que o primeiro alinhamento bem sucedido requeira ao menos quatro tentativas ?
\[ \mathbb{P}(X \ge 3) = 1 - \mathbb{P}(X \le 2) = 1 - (\mathbb{P}(X = 0) + \mathbb{P}(X = 1) + \mathbb{P}(X = 2)) = 0.008 \]
x = seq(0,2,1)
p = 0.8
p_x = dgeom(x,p)
p_x[1] 0.800 0.160 0.0321 - sum(p_x)[1] 0.008n = 10
x = seq(0,n,1)
p = 0.80
p_x = dgeom(x,p)
plot(x,p_x,type='h',xlab='Números de tentativas falhas para o alinhamento bem sucedido',ylab='p_X(x)')
points(x,p_x,col=2)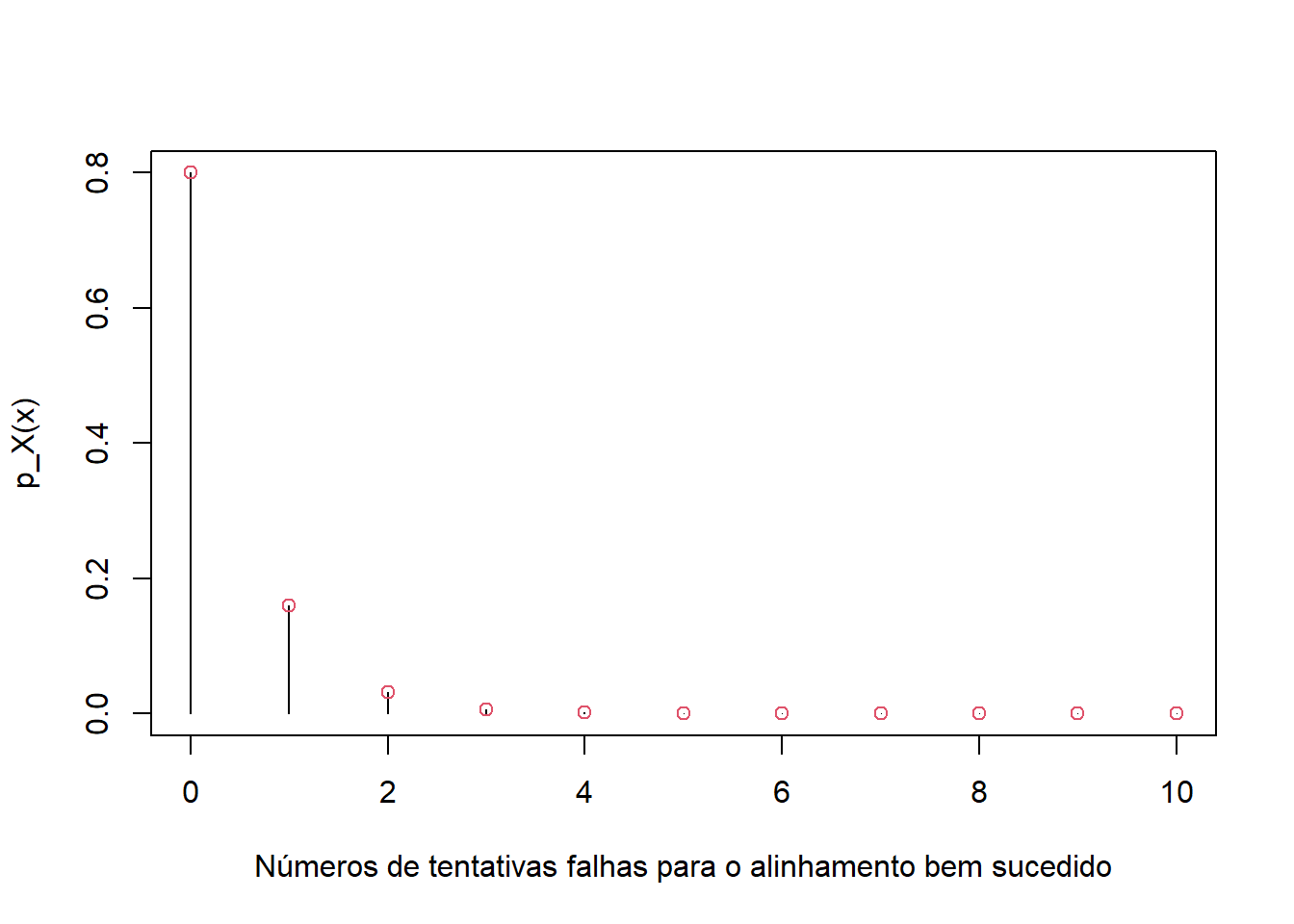
As probabilidades de cada um dos valores de \(x\) podem ser apresentadas:
library(knitr)
dx = data.frame(x, p_x) # agrupa os vetores x e p_x em um data frame
dx =round(dx,digits=4) # arredonda os valores do data frame
dx x p_x
1 0 0.8000
2 1 0.1600
3 2 0.0320
4 3 0.0064
5 4 0.0013
6 5 0.0003
7 6 0.0001
8 7 0.0000
9 8 0.0000
10 9 0.0000
11 10 0.0000Este conteúdo está disponível por meio da Licença Creative Commons 4.0
