Distribuição amostral da variância
Distribuição das variâncias de uma amostra aleatória de tamanho \(n\)
A distribuição das variâncias amostrais de uma variável aleatória representa a população de todas as possíveis variâncias oriundas de uma amostra aleatória de tamanho \(n\) de uma população, cuja a variável aleatória possui uma distribuição de densidade de probabilidade (falaremos aqui de variáveis aleatórias cuja resposta é continua).
Cabe mais uma vez relembrar aqui ao tomarmos uma amostra de uma população estaremos observando elementos (\(\omega_i\)) de uma população (\(\Omega\)), e que desses elementos temos interesse em analisar certa característica ou propriedade que nada mais é do que uma variável, neste caso aleatória, pois depende aleatóriamente do elemento que foi selecionado para compor a amostra.
Antes de mais nada cabe elucidar alguns cálculos fundamentais e isso exige do conhecimento das propriedades do valor esperado e das definições de parâmetros e estatísticas.
Considere o seguinte, ao calcularmos os parâmetros populacionais, como por exemplo a média populacional (\(\mu\)) ou a variância populacional (\(\sigma^2\)) ou ainda outro parâmetro, devemos, obviamente utilizar todos os elementos da população, dessa forma se repetidamente efetuarmos esse processo sob as mesmas condições, teremos sempre o mesmo resultado, ou seja uma constante. Na estatística clássica os parâmetros populacionais são constantes, e são calculados com todos os elementos da população, os \(N\) elementos.
No caso da variância populacional (\(\sigma^2\)), calcularemos da seguinte forma
\[ \begin{aligned} \sigma^2_{X} & = \frac{\sum(X- \mu)^2}{N}\\ \end{aligned} \]
onde:
\(N\) é o tamanho da população
\(X\) é a variável aleatória
\(\mu\) é o parâmetro média populacional, ou seja o \(E[X] = \mu\)
Como se chega a essa equação, apresentada acima ?
Bom, quando calculamos a variância de todos os elementos de uma variável aleatória (ex. a variabilidade da altura da população), estamos calculando de fato é o valor esperado dos desvio quadráticos \(E[(X-\mu)^2]\), que nada mais é do que a média dos desvios quadráticos. Lembre-se que o valor esperado dos desvios quadráticos é (para uma v.a. discreta e contínua):
\[ \begin{aligned} V(X) = E[(X-\mu)^2] &= \sum{(x_i-\mu)^2}p_X(x)\\ V(X) = E[(X-\mu)^2] &= \int{(x-\mu)^2}f_X(x) \end{aligned} \] Lembre-se que a distribuição de uma v.a. representa o comportamento do todo, ou seja da população, ou seja de todos os \(N\) elementos. Assim, a \(V(X)\) é uma propriedade da v.a. de todos os \(N\) elementos.
Bom, uma vez que possuímos todos os elementos (ou seja os dados relativos a v.a.), podemos calcular diretamente essa propriedade, neste caso a \(\sigma^2\).
Agora, e se não tivessemos acesso a toda a população e sim somente uma amostra da mesma? Neste caso eu não tenho como calcular a variância populacional \(\sigma^2\), mas tenho como calcular a variância amostral, a pergunta é, como ?
Bom, sabemos agora que não vamos lidar com uma constante, e sim com uma variável aleatória, pois os valores agora dependem da amostra, que é aleatória, estaremos calculando aquilo que chamamos de estatística. Sendo assim, essa quantidade que iremos calcular é uma v.a. com alguma distribuição.
Mais uma vez estaremos fazendo uma estimativa do parâmetro populacional. A forma de calcularmos essa estatística (v.a., que chamaremos de \(S^2\)) de forma apropriada é de esperar que na média, essa estatística calculada seja igual ao valor do parâmetro populacional (a constante \(\sigma^2\)), ou seja, esperamos que \(E[S^2] = \sigma^2\).
A forma apropriada de esperarmos esse resultado é quando calculamos essa estatística da seguinte forma:
\[ \begin{aligned} S^2 & = \frac{\sum(X- \overline{X})^2}{n-1}\\ \end{aligned} \]
onde:
\(n\) é o tamanho da amostra aleatória
\(X\) é a variável aleatória
\(\overline{X}\) é a variável aleatória média amostral
\((n-1)\) é chamado de graus de liberdade
Cabe notar que não temos neste caso o valor do parâmetro média populacional \(\mu\), e sendo assim utilizamos a sua estimativa \(\overline{X}\).
Porque dividimos a equação por \((n-1)\) ao invés de simplesmente \(n\) ?
Bom para respondermos a essa questão observe os seguintes resultados. A prova desses resultados virá em seguida.
\[\begin{align} E\Bigg[\frac{\sum_{i=1}^n (X_i-\color{red}{\mu})^2}{\color{blue}{n}}\Bigg] &= \sigma^2\\ E\Bigg[\frac{\sum_{i=1}^n (X_i-\color{red}{\overline{X}})^2}{\color{blue}{n}}\Bigg] &= \Bigg(\color{blue}{\frac{n-1}{n}} \Bigg)\sigma^2\\ E\Bigg[\frac{\sum_{i=1}^n (X_i-\color{red}{\overline{X}})^2}{\color{red}{n-1}}\Bigg] &= \sigma^2\\ \end{align}\]
Note que o valor esperado da equação (2) é um valor de variância viesado pelo termo \((n-1)/n\), e uma das soluções (matemática) para esse caso é dividir a equação por \((n-1)\) ao invés de simplesmente \(n\).
Prova
A seguir a prova da equação (1) \[ \begin{aligned} E\Bigg[\frac{\sum_{i=1}^n (X_i-\color{red}{\mu})^2}{\color{blue}{n}}\Bigg] &= \sigma^2\\ \end{aligned} \]
Primeiramente considere \(X_1, ..., X_n\) variáveis aleatórias, independentes e identicamente distribuidas (i.i.d), com média \(\mu\) e variância \(\sigma^2\).
Por regra geral (estatística clássica), temos que \(\mu\) e \(\sigma^2\) são constantes.
Na prova faremos uso dos seguintes resultados auxiliares.
\[ \begin{aligned} E[X] &= \mu\\ E[X-\mu] &= 0\\ \\ V[X] &= \sigma^2\\ V[X] &= E[(X-\mu)^2]\\ V[X] &= E[X^2] - (E[X])^2\\ V[X] &= E[X^2] - \mu^2\\ \\ E[X^2] &= V[X] + \mu^2\\ E[X^2] &= \sigma^2 + \mu^2\\ \\ V\Big[\overline{X}\Big] &= \frac{\sigma^2}{n}\\ V\Big[\overline{X}\Big] &= E\Big[\overline{X}^2\Big] - \Big(E\Big[\overline{X}\Big]\Big)^2\\ V\Big[\overline{X}\Big] &= E\Big[\overline{X}^2\Big] - \mu^2\\ \\ E\Big[\overline{X}^2\Big] &= V\Big[\overline{X}\Big] + \mu^2\\ E\Big[\overline{X}^2\Big] &= \frac{\sigma^2}{n} + \mu^2\\ \end{aligned} \]
\(E[X-\mu] = 0\), pois é propriedade da média, de se colocar exatamente no “centro de gravidade” dos dados, onde o somatório dos desvios é zero
Iniciaremos a análise verificando o que se espera dos desvios quadráticos em torno da média populacional.
\[ \begin{aligned} E[\sum_{i=1}^n (X_i-\mu)^2] &= E[\sum_{i=1}^n (X_i-\mu)^2]\\ &= \sum_{i=1}^n E[(X_i-\mu)^2]\\ &= \sum_{i=1}^n E[X_i^2 -2X_i\mu+\mu^2]\\ &= \sum_{i=1}^n E[X_i^2] -2\mu \sum_{i=1}^nE[X_i] + \sum_{i=1}^nE[\mu^2]\\ \end{aligned} \]
Assim temos,
\[\sum_{i=1}^nE[\mu^2] = n \cdot \mu^2\]
\[\sum_{i=1}^n E[X_i] = n \cdot \mu\]
\[\sum_{i=1}^nE[X^2] = n \cdot (\sigma^2 + \mu^2)\] \[ \begin{align} E[\sum_{i=1}^n (X_i-\mu)^2] &= n(\sigma^2 + \mu^2) - 2 n \mu^2 + n \mu^2\\ &= n\sigma^2\\ \end{align} \] Portanto é de se esperar que \[ E\Bigg[\frac{\sum_{i=1}^n (X_i-\mu)^2}{n}\Bigg] = \sigma^2 \]
Prova
A seguir a prova da equação (2) \[ \begin{aligned} E\Bigg[\frac{\sum_{i=1}^n (X_i-\color{red}{\overline{X}})^2}{\color{blue}{n}}\Bigg] &= \Bigg(\frac{\color{blue}{n-1}}{\color{blue}{n}} \Bigg)\sigma^2\\ \end{aligned} \]
\[ \begin{aligned} E\bigg[\sum_{i=1}^n (X_i -\overline{X})^2\bigg] &= E\bigg[\sum_{i=1}^nX_i^2 -2\overline{X}\sum_{i=1}^nX_i + \sum_{i=1}^n \overline{X}^2 \bigg] \\ &= E\bigg[\sum_{i=1}^nX_i^2 -2\overline{X}\sum_{i=1}^nX_i + n \cdot \overline{X}^2 \bigg] \end{aligned} \]
Mas como:
\[
\begin{aligned}
\overline{X}=\frac{\sum_{i=1}^n X_i}{n} \Longrightarrow \sum_{i=1}^n X_i=n\cdot \overline{X}
\end{aligned}
\] Substituindo \(\sum_{i=1}^n X_i\) temos:
\[ \begin{aligned} E\bigg[\sum_{i=1}^n (X_i -\overline{X})^2\bigg] &= E\bigg[\sum_{i=1}^nX_i^2 -2n\overline{X}^2 + n\overline{X}^2 \bigg] \\ &= E\bigg[\sum_{i=1}^nX_i^2 -n\overline{X}^2 \bigg] \\ &= \sum_{i=1}^nE[X_i^2]-nE[\overline{X}^2]\\ &= n \cdot(\sigma^2+\mu^2)-n \cdot\bigg(\frac{\sigma^2}{n}+\mu^2\bigg)\\ &= n\sigma^2 + n\mu^2 -\sigma^2-n\mu^2 \\ &= n\sigma^2-\sigma^2\\ &=(n-1)\cdot \sigma^2 \end{aligned} \]
Portanto nos temos que: \[E\bigg[\sum_{i=1}^n (X_i -\overline{X})^2\bigg] = (n-1)\cdot \sigma^2\]
Logo: \[ \begin{aligned} E\bigg[\frac{\sum_{i=1}^n (X_i -\overline{X})^2}{n}\bigg] = \frac{(n-1)}{n} \cdot \sigma^2 \end{aligned} \]
Prova
A seguir a prova da equação (3) \[ \begin{aligned} E\Bigg[\frac{\sum_{i=1}^n (X_i-\color{red}{\overline{X}})^2}{\color{blue}{n-1}}\Bigg] &= \sigma^2\\ \end{aligned} \]
Dada as provas anteriores note que:
\[ \begin{aligned} E\bigg[\sum_{i=1}^n (X_i -\overline{X})^2\bigg] &= (n-1)\cdot \sigma^2\\ \\ E\bigg[\frac{\sum_{i=1}^n (X_i -\overline{X})^2}{n-1}\bigg] &= \sigma^2 \end{aligned} \]
De onde temos a fórmula para calcular a variância a partir de uma amostra:
Variância amostral \[ \begin{aligned} S^2 = \frac{\sum_{i=1}^n (X_i -\overline{X})^2}{n-1} \end{aligned} \]
Precisamos verificar como a variável aleatória \(S^2\) se distribui
Vamos assumir que a variável aleatória (\(X\)) possui distribuição normal, para que matemáticamente os resultados sejam convenientes, assim temos que:
Seja \(X\) uma variável aleatória, \(X \sim N(\mu,\sigma^2)\), a distribuição da variância amostral segue uma distribuição desconhecida, por assim dizer, que quando reescalada segue uma qui-quadrado com \(n-1\) graus de liberdade.
\[ \begin{aligned} S^2 & = \frac{\sum(X- \overline{X})^2}{n-1}\\ E[S^2] & = \sigma^2 \\ V(S^2) & = \frac{2\sigma^4}{n-1}\\ \\ S^2 &\sim ~?\\ \small{\text{reescalada pela constante}} & ~\small{(n-1)/\sigma^2}\\ \\ \color{orange}{\frac{(n-1)}{\sigma^2}}S^2 &\sim ~ \chi^2_{(n-1)}\\ \end{aligned} \]Isso significa dizer que se a população do qual são retiradas as amostras segue uma distribuição de probabilidade normal, a variável aleatória \(S^2\) com média \(\sigma^2\) e desvio padrão \(2\sigma^4/{n-1}\), quando reescalada pela constante \((n-1)/\sigma^2\) tenderá à uma distribuição qui-quadrado com \(n-1\) graus de liberdade.
O seguinte teorema auxilia a entender esses resultados
Seja \(X_1, X_2, ..., X_n\) observações de uma amostra aleatória de tamanho \(n\) oriunda de uma distribuição normal \(X_i \sim N(\mu,\sigma^2)\).
\(\overline{X} = \frac{\sum{X_i}}{n}\) é a média amostral de \(n\) observações
\(S^2 = \frac{\sum(X- \overline{X})^2}{n-1}\) é a variância amostral de \(n\) observações
Então, temos que:
\(\overline{X}\) e \(S^2\) são independentes
\(\frac{(n-1)S^2}{\sigma^2} = \frac{\sum(X- \overline{X})^2}{\sigma^2} \sim \chi^2_{(n-1)}\)
Alguns resultados já conhecidos nos auxiliam nesta nova verificação, vamos à alguns deles:
\[ \begin{aligned} \color{blue}{X} &\sim N(\mu,\sigma^2)\\ \\ \color{orange}{Z} &= \frac{\color{blue}{X} - \mu}{\sigma}\\ \color{orange}{Z} &\sim N(0,1)\\ \\ \color{orange}{Z}^2 &= \Bigg(\frac{\color{blue}{X} - \mu}{\sigma}\Bigg)^2\\ \color{orange}{Z}^2 &\sim \chi^2_{(1)}\\ \\ Q &= \sum_{i=1}^{n}\color{orange}{Z}^2 = \sum_{i=1}^{n}\Bigg(\frac{\color{blue}{X_i} - \mu}{\sigma}\Bigg)^2\\ Q &\sim \chi^2_{(n)}\\ \\ \end{aligned} \]
Re-arranjando a equação da variância amostral:
\[ \begin{aligned} S^2 = \frac{\sum_{i=1}^n (X_i -\overline{X})^2}{n-1}\\ (n-1)S^2 = \sum_{i=1}^n (X_i -\overline{X})^2\\ \end{aligned} \]
Podemos simplesmente dividir essa equação por uma constante, neste caso \(\color{red}{\sigma^2}\), note que a forma da distribuição não irá se alterar, somente seus valores numéricos, convenientemente teríamos:
\[ \begin{aligned} \frac{(n-1)S^2}{\color{red}{\sigma^2}} = \frac{\sum_{i=1}^n (X_i -\overline{X})^2}{\color{red}{\sigma^2}}\\ \\ \frac{(n-1)S^2}{\color{red}{\sigma^2}} = \sum_{i=1}^{n}\Bigg(\frac{X_i -\overline{X}}{\color{red}{\sigma}}\Bigg)^2\\\\ \end{aligned} \]
Vamos primeiramente tentar encontrar alguma relação com aquilo que já conhecemos como distribuição, como é o caso da distribuição de \(\color{orange}{Z}^2\).
\[ \begin{aligned} Q = \sum_{i=1}^{n}\color{orange}{Z}^2 &= \sum_{i=1}^{n}\Bigg(\frac{\color{blue}{X_i} - \mu}{\sigma}\Bigg)^2\\ \end{aligned} \]
Um pequeno artifício matemático pode ser lançado aqui, observe que podemos somar \(0\) à equação \((-\overline{X} + \overline{X})\):
\[ \begin{aligned} Q = \sum_{i=1}^{n}\color{orange}{Z}^2 &= \sum_{i=1}^{n}\Bigg(\frac{\color{blue}{X_i} - \mu}{\sigma}\Bigg)^2\\ Q &= \sum_{i=1}^{n}\Bigg(\frac{\color{blue}{X_i} - \mu -\overline{X} + \overline{X}}{\sigma}\Bigg)^2\\ Q &= \sum_{i=1}^{n}\Bigg(\frac{(\color{blue}{X_i} -\overline{X}) + (\overline{X} - \mu)}{\sigma}\Bigg)^2\\ Q &= \sum_{i=1}^{n}\Bigg(\frac{\color{blue}{X_i} -\overline{X}}{\sigma}\Bigg)^2 + \sum_{i=1}^{n}\Bigg(\frac{\overline{X}- \mu}{\sigma}\Bigg)^2 + 2\Bigg(\frac{\overline{X}- \mu}{\sigma^2}\Bigg) \sum_{i=1}^{n}\Big(\color{blue}{X_i} -\overline{X}\Big)\\ \end{aligned} \]
Uma vez que,
\[ \begin{aligned} \sum_{i=1}^{n}\Big(\color{blue}{X_i} -\overline{X}\Big) = n\overline{X} - n\overline{X} = 0\\ \end{aligned} \]
Dessa forma, \(Q\) se reduz a,
\[ \begin{aligned} Q &= \sum_{i=1}^{n}\Bigg(\frac{\color{blue}{X_i} -\overline{X}}{\sigma}\Bigg)^2 + \sum_{i=1}^{n}\Bigg(\frac{\overline{X}- \mu}{\sigma}\Bigg)^2\\ Q &= \frac{\sum_{i=1}^{n}\Big(\color{blue}{X_i} -\overline{X}\Big)^2}{\sigma^2} + \frac{n(\overline{X}- \mu)^2}{\sigma^2}\\ \end{aligned} \]
A média amostral \(\overline{X}\) é uma variável aleatória que se distribui de forma normal, de acordo com o TLC (Teorema do Limite Central), e os resultados a seguir já são conhecidos.
\[ \begin{aligned} \overline{X} &\sim N(\mu,\sigma^2/n)\\ \\ Z &= \Bigg(\frac{\overline{X}- \mu}{\sigma/ \sqrt{n}}\Bigg)\\ \\ Z &= \frac{\sqrt{n}(\overline{X} - \mu)}{\sigma}\\ \\ Z &\sim N(0,1)\\ \\ Z^2 &= \Bigg(\frac{\overline{X}- \mu}{\sigma/ \sqrt{n}}\Bigg)^2\\ \\ Z^2 &= \frac{n(\overline{X}- \mu)^2}{\sigma^2}\\ \\ Z^2 &\sim \chi^2_{(1)}\\ \end{aligned} \]
Aplicando o conhecimento das distribuições temos que:
\[\begin{aligned} \underbrace{Q}_{\sim \chi^2_{(n)}} &= \frac{\sum_{i=1}^{n}\Big(\color{blue}{X_i} -\overline{X}\Big)^2}{\sigma^2} + \underbrace{\frac{n(\overline{X}- \mu)^2}{\sigma^2}}_{\sim \chi^2_{(1)}}\\ \\ \underbrace{\frac{\sum_{i=1}^{n}\Big(\color{blue}{X_i} -\overline{X}\Big)^2}{\sigma^2}}_{\sim \chi^2_{(n-1)}} &= \underbrace{Q}_{\sim \chi^2_{(n)}} - \underbrace{\frac{n(\overline{X}- \mu)^2}{\sigma^2}}_{\sim \chi^2_{(1)}}\\ \end{aligned}\]Dessa forma, quando a amostra for oriunda de uma distribuição normal, a quantidade relacionada a variância amostral irá se distribuir do forma qui-quadrado com \(n-1\) graus de liberdade,
\[ \begin{aligned} \frac{\sum_{i=1}^{n}\Big(\color{blue}{X_i} -\overline{X}\Big)^2}{\sigma^2} &= \color{green}{\frac{(n-1)S^2}{\sigma^2}} \sim \chi^2_{(n-1)}\\ \end{aligned} \]
library(ggplot2)
ggplot(data.frame(x = c(0, 30)), aes(x = x)) +
stat_function(fun = dchisq, args = list(df = 1),aes(colour = "(n-1) = 1"), size = 1.5) +
stat_function(fun = dchisq, args = list(df = 3),aes(colour = "(n-1) = 3"), size = 1.5) +
stat_function(fun = dchisq, args = list(df = 8),aes(colour = "(n-1) = 8"), size = 1.5) +
scale_x_continuous(name = expression(paste({chi^{2}}[(n-1)])),
breaks = seq(0, 30, 5),
limits=c(0, 30)) +
scale_y_continuous(name = "Densidades") +
ggtitle("Distribuições Qui-quadrado com diferentes graus de liberdade (n-1)") +
scale_colour_brewer(palette="Accent") +
labs(colour = "Groups") +
theme_bw() +
theme(axis.line = element_line(size=1, colour = "black"),
panel.grid.major = element_line(colour = "#d3d3d3"),
panel.grid.minor = element_blank(),
panel.border = element_blank(), panel.background = element_blank(),
plot.title = element_text(size = 14, family = "Tahoma", face = "bold"),
text=element_text(family="Tahoma"),
axis.text.x=element_text(colour="black", size = 9),
axis.text.y=element_text(colour="black", size = 9),
legend.position = "bottom")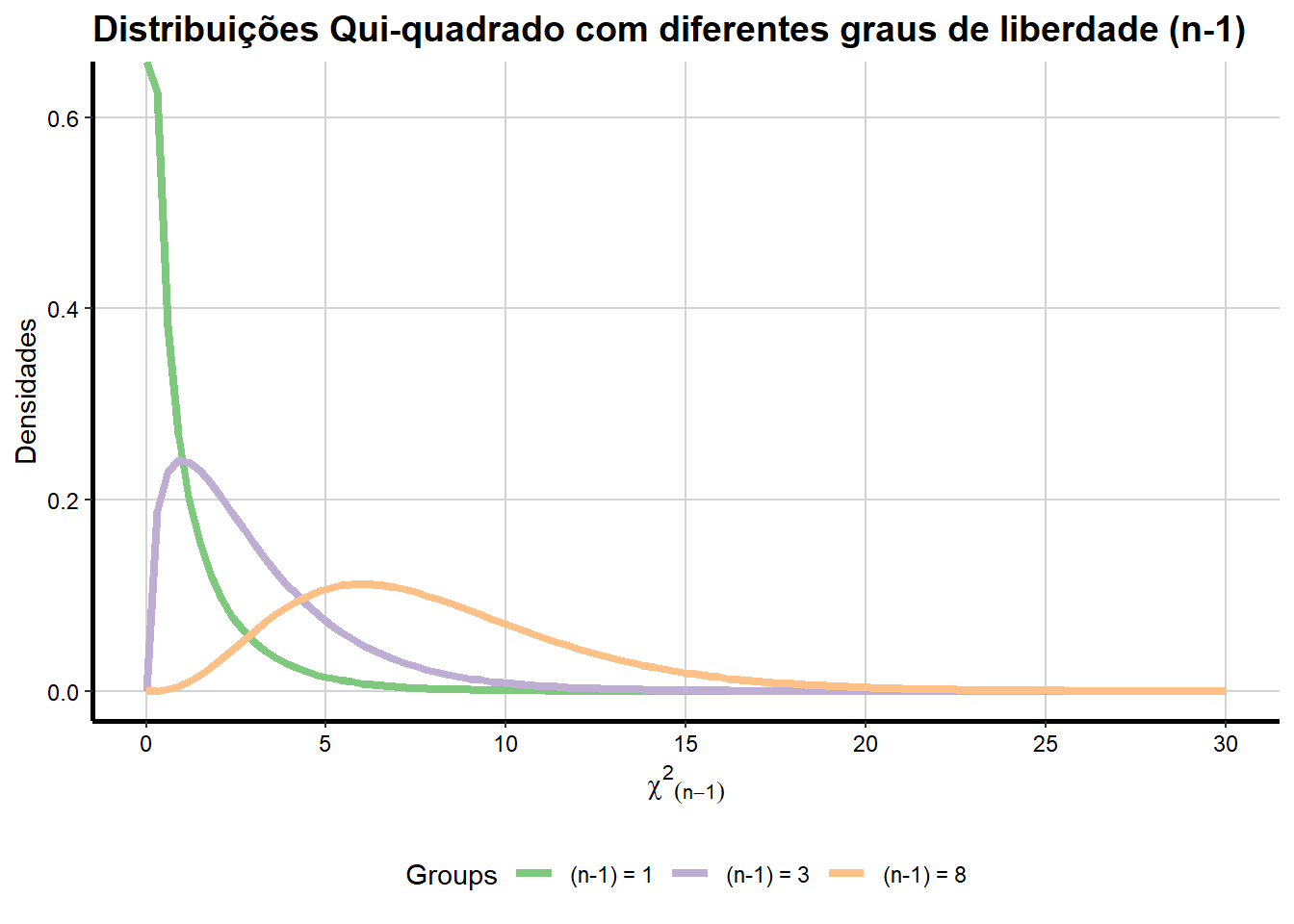
Exemplo 1
Assuma que nota dos alunos na disciplina de estatística é normalmente distribuida com média \(\mu = 7.2\) e variância \(\sigma^2 = 1.6^2\).
Seja \(X_i\) a nota de alunos aleatoriamente selecionados, \(i = 1,...,8\) na disciplina.
Qual é a distribuição de \(\frac{(n-1)S^2}{\sigma^2}\)?
Solução: Exemplo 1
Devido ao tamanho da amostra ser de \(n=8\) elementos da população o Teorema acima nos informa que:
\[ \begin{aligned} \frac{\sum_{i=1}^{n}\Big(\color{blue}{X_i} -\overline{X}\Big)^2}{\sigma^2} &= \color{green}{\frac{(n-1)S^2}{\sigma^2}}\\ \end{aligned} \]
\[ \begin{aligned} \frac{\sum_{i=1}^{n}\Big(\color{blue}{X_i} -\overline{X}\Big)^2}{\sigma^2} &= \color{green}{\frac{(n-1)S^2}{\sigma^2}} = \color{green}{\frac{(8-1)S^2}{1.6^2}} = = \color{green}{\frac{(7)S^2}{1.6^2}}\\ \end{aligned} \]
segue uma distribuição de qui-quadrado com \(gl = (n-1)=7\) graus de liberdade. Abaixo temos como a distribuição de densidades teórica se parece:
library(ggplot2)
ggplot(data.frame(x = c(0, 30)), aes(x = x)) +
stat_function(fun = dchisq, args = list(df = 7),aes(colour = "(n-1) = 7"), size = 1.5) +
scale_x_continuous(name = expression(paste({chi^{2}}[(7)])),
breaks = seq(0, 30, 5),
limits=c(0, 30)) +
scale_y_continuous(name = "Densidades") +
ggtitle("Distribuições Qui-quadrado com grau de liberdade (n-1 = 7)") +
scale_colour_brewer(palette="Accent") +
labs(colour = "Groups") +
theme_bw() +
theme(axis.line = element_line(size=1, colour = "black"),
panel.grid.major = element_line(colour = "#d3d3d3"),
panel.grid.minor = element_blank(),
panel.border = element_blank(), panel.background = element_blank(),
plot.title = element_text(size = 14, family = "Tahoma", face = "bold"),
text=element_text(family="Tahoma"),
axis.text.x=element_text(colour="black", size = 9),
axis.text.y=element_text(colour="black", size = 9),
legend.position = "none")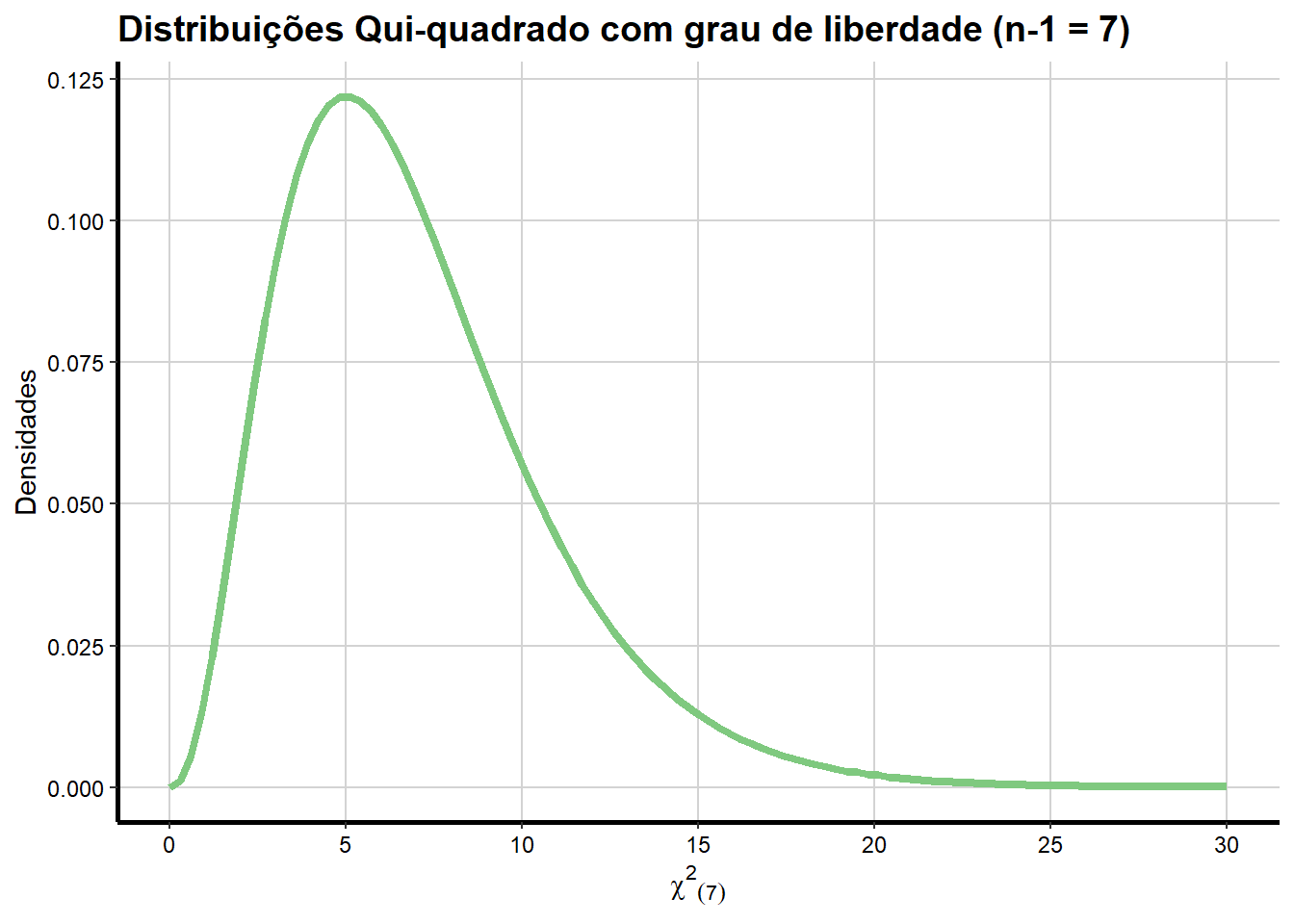
Mais uma vez, todo o trabalho que foi feito até agora sobre tem sido de natureza teórica. Isto é, o que aprendemos é baseado na teoria da probabilidade. Sendo assim neste caso veríamos esses resultado se obtivéssemos repetidas amostras de tamanho 8, digamos 1000 amostras de tamanho 8 e calculássemos a quantidade:
\[ \frac{(8-1)S^2}{1.6^2} = \frac{\sum_{i=1}^{n}\Big(\color{blue}{X_i} -\overline{X}\Big)^2}{1.6^2} \]
para cada amostra.
Ou seja, a distribuição dos 1000 valores resultantes da função acima deve se parecer com uma distribuição qui-quadrado (7)??
A única maneira de responder a essa pergunta é simular esses resultados.
Abaixo seguem alguns resultados de uma simulação (neste caso somente são apresentados as 6 primeiras amostras simuladas de tamanho 8), onde foram gerados 1000 amostras de tamanho \(n=8\) a partir de uma distribuição normal com média \(\mu = 100\) e variância \(\sigma^2 = 1.6^2\).
Na tabela abaixo é apresentado somente 6 das amostras de tamanho 8, como exemplo do conjunto resultante dessa simulação de 1000 amostras. Note que \(X1 ... X8\) são as variáveis aleatórias normais, \(n=8\) e a chamada quantidade é exatamente
\[ \frac{(8-1)S^2}{1.6^2} \] a quantidade calculada para cada amostra de tamanho 8.
md.pop = 7.2 #média populacional \mu
var.pop = 1.6^2 #variância populacional \sigma^2
dp.pop = 1.6 #desvio padrão populacional \sigma
n = 8
df = data.frame(matrix(rnorm(8000, mean = md.pop, sd = dp.pop), nrow = 1000))
df$"media.a" = apply(df[1:8], 1, function(x) mean(x))
df$"variancia.a" = apply(df[1:8], 1, function(x) var(x))
df$"quantidade" = apply(df[1:8], 1, function(x) (n-1)*var(x)/var.pop)
kable(head(df))| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | media.a | variancia.a | quantidade |
|---|---|---|---|---|---|---|---|---|---|---|
| 6.396492 | 8.956240 | 9.358181 | 7.080006 | 9.603621 | 7.883360 | 6.442272 | 4.614644 | 7.541852 | 2.995690 | 8.191341 |
| 7.410450 | 9.089658 | 6.832411 | 5.684667 | 6.762497 | 6.829758 | 7.241935 | 8.302194 | 7.269196 | 1.079032 | 2.950479 |
| 7.073733 | 8.140017 | 4.428024 | 7.200601 | 6.360233 | 7.846389 | 6.449531 | 6.089038 | 6.698446 | 1.355920 | 3.707594 |
| 8.618856 | 8.921876 | 6.196306 | 4.760068 | 6.993306 | 6.320126 | 5.371091 | 6.157524 | 6.667394 | 2.131127 | 5.827301 |
| 7.387154 | 9.018645 | 6.815188 | 7.357363 | 6.467231 | 6.090975 | 7.949740 | 6.639526 | 7.215728 | 0.879498 | 2.404877 |
| 7.709808 | 8.416468 | 5.059876 | 4.757428 | 7.642667 | 5.003896 | 8.028996 | 8.087191 | 6.838291 | 2.533213 | 6.926755 |
Por exemplo, note que para a primeira linha temos como média amostral \(\overline{x} = 7.5418521\) e variância amostral \(s^2 = 2.9956904\).
\[ \begin{aligned} \frac{\sum_{i=1}^{n}\Big(\color{blue}{X_i} -\overline{X}\Big)^2}{\sigma^2} &= \color{green}{\frac{(8-1)S^2}{1.6^2} =} \color{green}{\frac{(7)2.9956904}{1.6^2} = 8.191341} \\ \end{aligned} \] Bom, agora que temos os valores dessa quantidade calculada para cada amostra podemos observar a sua distribuição empírica.
ggplot(df, aes(df$quantidade)) +
geom_histogram(aes(y=..density..),binwidth = 1) +
# stat_function(fun = dchisq, args = list(df = 7), aes(colour = "Qui-quadrado_(n-1=7)"), size = 1.5) +
scale_x_continuous(name = expression(paste(frac((7)*S^{2},1.6^{2}))),
breaks = seq(0, 30, 5),
limits=c(0, 30)) +
scale_y_continuous(name = "Densidades") +
ggtitle("Histograma da quantidade") +
scale_colour_brewer(palette="Accent") +
labs(colour = "Groups") +
theme_bw() +
theme(axis.line = element_line(size=1, colour = "black"),
panel.grid.major = element_line(colour = "#d3d3d3"),
panel.grid.minor = element_blank(),
panel.border = element_blank(), panel.background = element_blank(),
plot.title = element_text(size = 14, family = "Tahoma", face = "bold"),
text=element_text(family="Tahoma"),
axis.text.x=element_text(colour="black", size = 9),
axis.text.y=element_text(colour="black", size = 9),
legend.position = "none")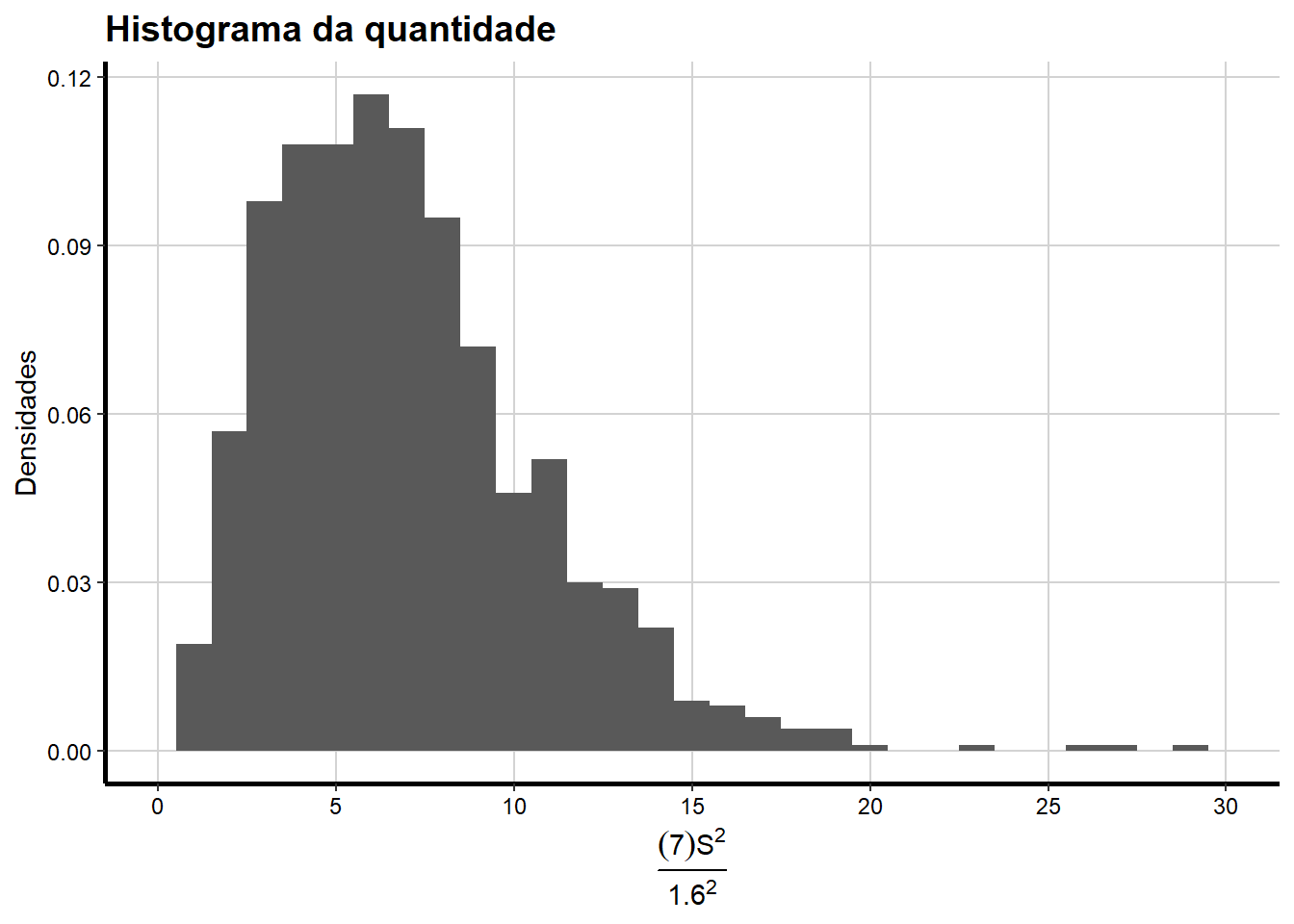
Se impusermos no gráfico uma curva das densidades de uma \(\chi^2_{7}\) com 7 graus de liberdade temos:
ggplot(df, aes(df$quantidade)) +
geom_histogram(aes(y=..density..),binwidth = 1) +
stat_function(fun = dchisq, args = list(df = 7), aes(colour = "Qui-quadrado_(n-1=7)"), size = 1.5) +
scale_x_continuous(name = expression(paste(frac((7)*S^{2},1.6^{2}))),
breaks = seq(0, 30, 5),
limits=c(0, 30)) +
scale_y_continuous(name = "Densidades") +
ggtitle("Histograma da quantidade") +
scale_colour_brewer(palette="Accent") +
labs(colour = "Groups") +
theme_bw() +
theme(axis.line = element_line(size=1, colour = "black"),
panel.grid.major = element_line(colour = "#d3d3d3"),
panel.grid.minor = element_blank(),
panel.border = element_blank(), panel.background = element_blank(),
plot.title = element_text(size = 14, family = "Tahoma", face = "bold"),
text=element_text(family="Tahoma"),
axis.text.x=element_text(colour="black", size = 9),
axis.text.y=element_text(colour="black", size = 9),
legend.position = "none")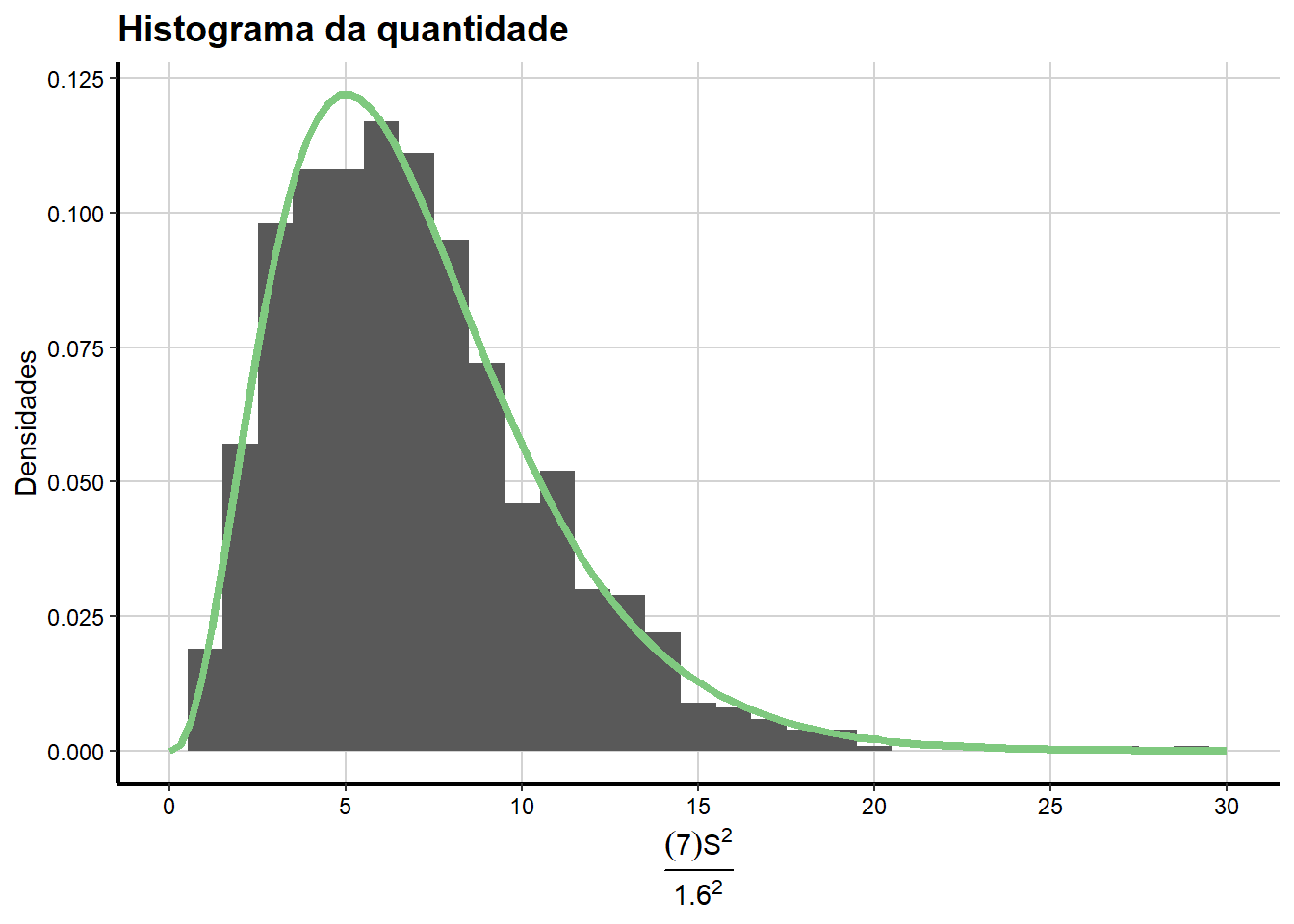
Que é muito similar a distribuição da quantidade em questão, que é relacionada com a variância amostral.
Applet de simulação da distribuição amostral
Abaixo está disponível um applet em Java que simula o processo de tomada de amostras de tamanho \(n\) e a criação da distribuição amostral.
Está disponível a simulação da distribuição amostral das seguintes v.a.s:
- Média
- Mediana
- sd - Desvio Padrão
- Variância
- Variância U (n-1)
- Amplitude
Este applet java foi desenvolvido por David Lane (Rice University , University of Houston Clear Lake, and Tufts University), no projeto: Online Statistics Education: A Multimedia Course of Study (http://onlinestatbook.com/). Project Leader: David M. Lane, Rice University.