Distribuição Binomial
Esta importante distribuição é aplicada em casos de experimentos repetidos, onde existem dois possíveis resultados: cara ou coroa, sucesso ou fracasso, item defeituoso ou item não defeituoso, e muitos outros possíveis pares. A probabilidade de cada resultado pode ser calculada utilizando a regra da multiplicação, talvez com o uso do diagrama de árvore, porém é muito mais simples e eficiente utilizar uma equação generalizada.
Assim, uma variável aleatória poderá ter sua distribuição de probabilidade modelada de forma binomial caso atenda os seguintes pressupostos:
o resultado é completamente determinado por chance (aleatório);
existem somente dois possíveis resultados, experimento Bernoulli;
todas as tentativas possuem a mesma probabilidade para um resultado em particular. Ou seja, as tentativas ou realizações do experimento são independentes;
isso implica que, existe uma probabilidade \(p\) de sucesso constante em cada tentativa
o número de tentativas, \(n\), é um valor fixo, um número inteiro e positivo;
Dado um experimento aleatório \(e\), de acordo com a v.a.d. \(X\):
- Seja \(X\) o número de caras em \(n\) tentativas independentes.
- Seja \(X\) o número de itens defeituosos em \(n\) itens produzidos independentes.
- Seja \(X\) o número de amostras contaminada em \(n\) amostras independentes.
- Seja \(X\) o número de questões corretas em \(n\) questões respondidas independentes.
- …
O modelo é dado pela seguinte função massa de probabilidade (PMF):
\[ p_X(x) = \mathbb{P}(X=x)=\left(\begin{array}{c}n\\x\end{array}\right) p^x(1-p)^{n-x} \]
onde,
\[ \left(\begin{array}{c}n\\x\end{array}\right)=\frac{n!}{x!(n-x)!} \] para \(x = 0,1,\ldots,n\):
Exemplo Binomial 1:
Baseado em estudos anteriores, a probabilidade de um certo componente elétrico estar em condições operacionais satisfatórias é de 0.98. Os componentes são amostrados item por item, a partir de uma produção (contínua). Em uma amostra de cinco componentes, quais são as probabilidades de se encontrarem,
- zero
- exatamente um
- exatamente dois
- dois ou mais
- ao menos quatro, itens defeituosos?
Resposta Exemplo B1:
Os requisitos para a aplicação do modelo binomial foram satisfeitos. \(n=5\), \(P(defeituoso) = 0.02\) Assumiremos como \(p=0.02\) a probabilidade de encontrarmos um item defeituoso. Aplicando o modelo probabilístico binomial para responder as questões temos:
n = 5
p = 0.02
x = seq(0,n,1)
p_x = dbinom(x,n,p)
plot(x,p_x,type='h',xlab='valores de x',ylab='p_X(x)')
points(x,p_x,col=2)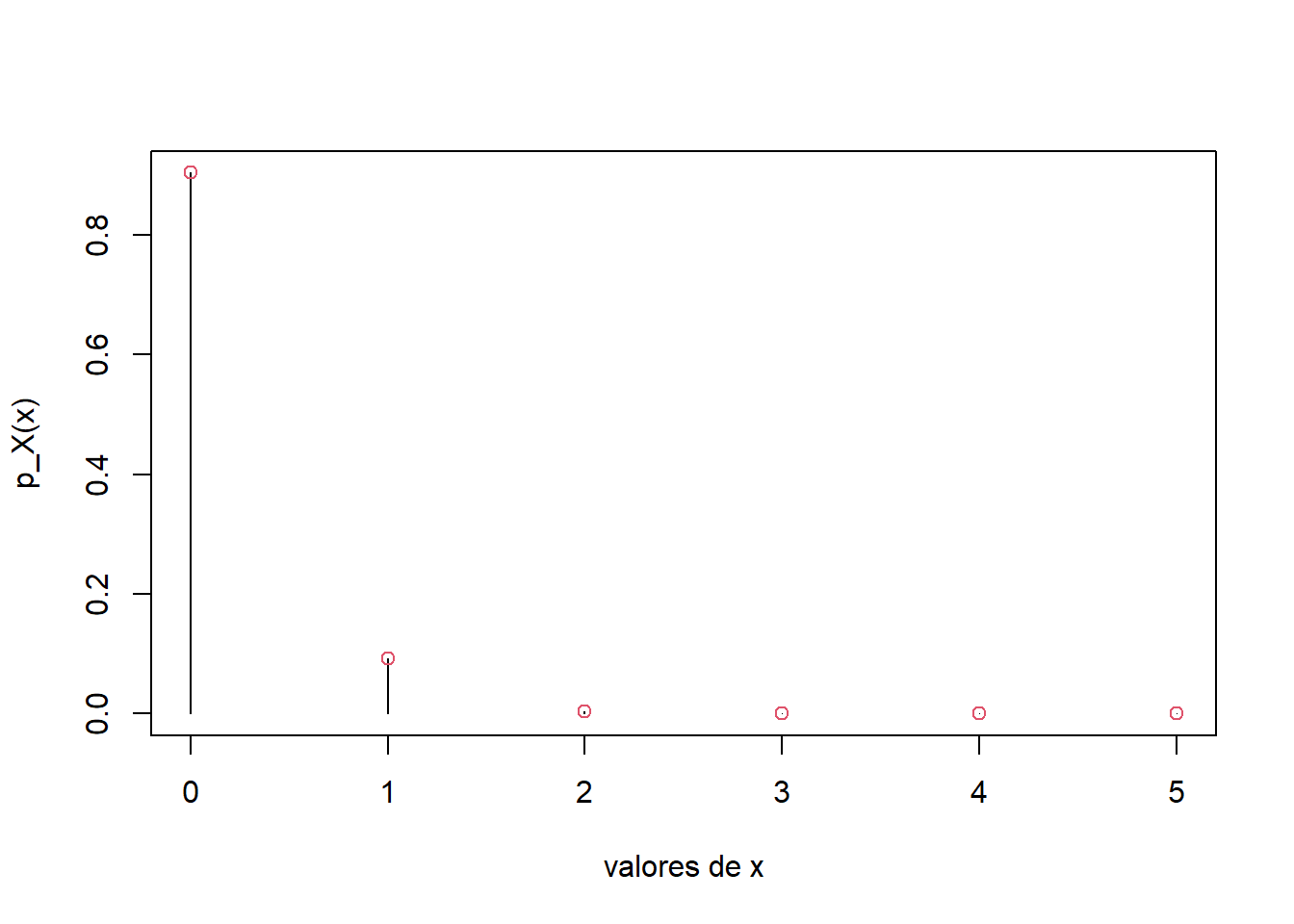
As probabilidades de cada um dos valores de \(x\) pode ser apresentadas:
setNames(p_x, x) 0 1 2 3 4 5
0.9039207968 0.0922368160 0.0037647680 0.0000768320 0.0000007840 0.0000000032 - zero
- exatamente um
- exatamente dois
- dois ou mais
- ao menos quatro, itens defeituosos?
a = p_x[1] # o primeiro elemento do vetor p_x, ou seja p_X(0)
b = p_x[2] # o segundo elemento do vetor p_x, ou seja p_X(1)
c = p_x[3] # o terceiro elemento do vetor p_x, ou seja p_X(2)
d = 1 - (p_x[1] + p_x[2]) # 1 - [p_X(0) + p_X(1)]
e = p_x[5] + p_x[6] # p_X(4) + p_X(5)
setNames(c(a,b,c,d,e), c('a','b','c','d','e')) a b c d e
0.9039207968 0.0922368160 0.0037647680 0.0038423872 0.0000007872
Este conteúdo está disponível por meio da Licença Creative Commons 4.0