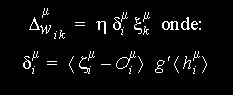INE 5443
3. Técnicas Subsimbólicas: Redes Neurais
Parte I:
3.1. Filosofia
Geral da Aplicação do Raciocínio
Subsimbólico
a Padrões: Redes Neurais Aprendendo Dados, Classificadores e
Agrupadores
3.2. O
Simulador SNNS - Stutgarter Neural Network Simulator
3.3. Classificadores:
Usando Aprendizado Supervisionado para Reconhecer Padrões
Parte II:
3.4. Desenvolvimento de Aplicações: Usando Aprendizado Supervisionado
Parte III:
3.5. Agrupadores:
Usando Aprendizado Não Supervisionado para Organizar
Padrões
3.5.1. O
Modelo de Kohonen e Quantização de Vetores
3.5.2. O
Modelo ART: Teoria da Ressonância Adaptativa
Parte IV:
3.6. Explorando
Dados Agrupados em Redes
3.1.
Filosofia Geral da Aplicação do Raciocínio
Subsimbólico
a Padrões: Redes Neurais Aprendendo Dados, Classificadores e
Agrupadores
Chamamos de Raciocínio
Subsimbólico ao procesamento de informação em
um nível onde os padrões representam conjuntos de dados
mas
onde não podemos associar um significado imediato a cada dado
processado.
Isto significa que trabalhamos com dados, que em seu conjunto podem ser
chamados de informação e assumir um significado, mas onde
não sabemos ou não podemos determinar o significado de
cada
parte do conjunto de informação em separado. O mesmo vale
para as representações internas, intermediárias
desses
dados: usamos sistemas que representam essa informação,
mas
eles são sistemas black box - caixa preta - produzindo
classificações
dos padrões e resultados numéricos, sem no entanto fazer
isto de forma explícita. As redes neurais são o melhor
exemplo
de um sistema subsimbólico: mesmo que cada parte de um
padrão
apresentado a uma rede tenha um significado explícito,
associável
a um símbolo de nosso modelo do mundo real, a
representação
interna dos dados no procesador (a rede) não é
explícita
e não possui significado. Um método subsimbólico
tipicamente
é incapaz de explicar porque chegou a uma determinada
conclusão,
uma vez que um mapeamento explícito de causa-e-efeito não
existe.
Fica mais fácil ilustrar este conceito através de um exemplo. Imagine um sistema militar para classificar tipos de navios ("inimigos") a partir do padrão de ruído emitido por estes, da forma como é captado por um submarino ("nosso"). Hipotetize que nós sabemos que um determinado padrão de ruídos corresponde a um porta-aviões de determinada classe de uma determinada nacionalidade. Este padrão inclue um conjunto de freqüências e as variações de amplitude dessas freqüências, além de algumas outras informações. Nós podemos associar um conjunto de símbolos a esse padrão: "Porta-Aviões modelo Banheirão de Corto Maltese", mas classificamos o padrão como um todo. Nós não sabemos dizer que papel tem uma freqüência X qualquer do ruído neste padrão ou que parte mecânica do navio em questão ela representa. Talvez não saibamos nem mesmo, se vamos continuar cnseguindo classificar o padrão, caso retiremos os valores correspondentes a esta freqüência do padrão.
Este é um exemplo típico. Mesmo em situações onde os dados possuem um significado conhecido, como no caso de dados de um paciente cardíaco potencial, onde eu sei o significado da freqüência cardíaca, mas onde eu não sei o relacionamento entre a freqüência cardíaca e a chance deste paciente ter um infarte numa determinada situação futura. É esse relacionamento, que eu não posso mapear de forma explícita que eu quero que um sistema subsimbólico mapeie implicitamente para mim. E os sistemas subsimbólicos fazem isto, mas o fazem de forma fechada, sem gerar mapas, tabelas estatísticas ou conjuntos de regras de como criam este mapeamento.
As Redes
Neurais Artificiais
são o mais difundido e popular conjunto de métodos
subsimbólicos,
sendo em geral caixas-pretas por excelência. Existem outros
métodos
que não vamos abordar aqui. O fato das redes neurais serem
caixas
pretas muitas vezes é citado como uma de suas desvantagens.
Neste
capítulo nós vamos ver que isto é relativo. Este
capítulo
pressupõe que você já viu Teoria das Redes Neurais
na cadeira de Inteligência Artificial e que você tem o
conhecimento
teórico básco sobre os métodos: aqui nós
vamo
ver aplicações de redes neurais e técnicas de
integração
das mesmas em sistemas mais complexos.
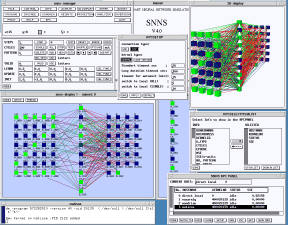
3.2. O Simulador SNNS - Stutgarter Neural Network Simulator
O SNNS é um dos melhores simuladores de Redes Neurais existentes. Porisso nós vamos vê-lo aqui. O objetivo de alocarmos um capítulo a ele é o de prover ao aluno com uma ferramenta poderosa para a execução dos exercícios propostos, livrando-o da necessidade de ter de programar ele mesmo as redes.O SNNS possui outra vantagem: após treinada um rede, você pode gerar com o SNNS um arquivo em linguagem "C" contendo a rede treinada. Este arquivo compilado pode ser utilizado como prorama standalone ou então como biblioteca (.dll ou .so) linkada ao programa aplicativo que você for usar. Isto é uma vantagem para as aplicações em Smalltalk que você vai desenvolver, pois permite que você utilize o pacote "DLL & C connect" para usar estas redes em Smalltalk.
- Versão do SNNS em Java para Windows
- Java Runtime Environment completo que você precisa para o software acima
- Versão compilada do SNNS 4.2 para Linux (se você possue RedHat ou Conectiva instalado pode ter problemas para rodar pois a versão do Athena suprida com RedHat e seus clones é meio estranha. Teste estas opções: a) Mude a profundidade de seu vídeo para 8 bits ou b) Não carregue os arquivos de configuração dos exemplos, apenas as redes e os arquivos de treinamento.
- Versão do SNNS para SunOS ou Solaris: Os fontes do SNNS compilam sem problemas nas plataformas Sun. Acesse a homepage do SNNS e baixe os fontes. As bibliotecas do Athena podem ser baixadas para Sun em vários lugares.
3.3. Classificadores: Usando Aprendizado Supervisionado para Reconhecer Padrões
Há dois modelos de redes neurais utilizados na prática como classificadores passíveis de serem gerados através de aprendizado supervisionado. Ambos os modelos baseiam-se nos Perceptrons feed-forward 1 , variando o número de camadas e a função de ativação e, por conseguinte, a regra de aprendizado: a) As Redes Backpropagation 2 e b) as Redes de Base Radial.Por serem as mais utilizadas e, do ponto de vista prático, mas mais importantes, vamos nos ocupar aqui das Redes Backpropagation, também chamadas redes-BP. As redes de Base Radial, conhecidas também por redes-RBF podem ser usadas, em teoria, para representar os mesmos tipos de problemas que uma rede Backpropagation equivalente. Alguns autores argumentam que são mais eficientes durante o treinamento. Por outro lado, a compreensão de seu algoritmo de aprendizado envolve uma matemática bastante mais complexa. Como são utilizadas para resolver o mesmo tipo de problemas que os onde Backpropagation encontra aplicação, sem vantagens consideráveis na qualidade do resultado final, vamos ignorá-las aqui. No final desta seção há uma comparação entre redes-RBF e redes-BP, extraída de [Haykin] e um comentário nosso sobre redes-RBF e sua relação com Nearest Neighbour e métodos que utilizam NN, como IBL*.
Como
esta disciplina pressupõe que você já viu o assunto
Redes Neurais, vamos aqui apenas recordar alguns conceitos
matemáticos
importantes para que você entenda a nossa discussão mais
adiante
de como se deve aplicar corretamente Backpropagation.
3.3.1. Princípios Matemáticos de Redes-BP
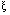 e vetor de saída
e vetor de saída 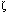 . O
vetor
de saída representa a atividades esperada nos neurônios de
saída quando é apresentado o vetor de entrada nos
neurônios
de entrada da rede.
. O
vetor
de saída representa a atividades esperada nos neurônios de
saída quando é apresentado o vetor de entrada nos
neurônios
de entrada da rede.


Princípios Básicos das Redes Backpropagation
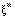 gerada por este padrão na camada de neurônios de entrada,
camada a camada, até gerarmos uma ativação nos
neurônios
da camada de saída.
gerada por este padrão na camada de neurônios de entrada,
camada a camada, até gerarmos uma ativação nos
neurônios
da camada de saída.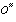 gerada para o vetor de entrada
gerada para o vetor de entrada 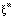 do padrão m pela rede seja o mais próximo possível
do vetor de saída
do padrão m pela rede seja o mais próximo possível
do vetor de saída 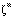 deste
padrão, de forma que no futuro, quando apresentarmos um outro
vetor
similar a
deste
padrão, de forma que no futuro, quando apresentarmos um outro
vetor
similar a 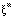 , a rede produza
uma
resposta o mais próxima possível de
, a rede produza
uma
resposta o mais próxima possível de 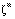 .
. 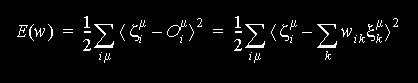
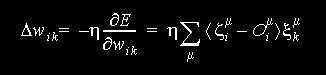
- introduzimos uma taxa de aprendizado h, tipicamente de valor < 0,2
- apresentamos os padrões de treinamento em ordem aleatória, garantindo que tenhamos apresentado todos antes de reapresentarmos algum.
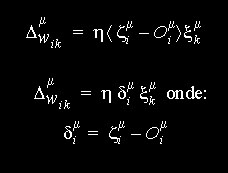
Aprendizado das Redes-BP
- para que uma rede neural feedforward possa representar uma função qualquer (universalidade representacional) ela necessita de pelo menos uma camada intermediária, além da camada de entrada e da de saída e a função de ativação de pelo menos parte dos neurônios deve ter caráter não-linear.
- para que a rede possa aprender, é necesário que possamos calcular a derivada do erro em relação aos pesos em cada camada, de tràs para frente, de forma a minimizar a função custo definida na camada de saída. Para isto ser possível, a função de ativação deve ser derivável.
- introduzir uma não linearidade sem no entanto alterar de forma radical a resposta da rede (ela se comporta de forma similar a uma rede linear para casos "normais") e
- possibilitar o cálculo da derivada parcial do erro em relação aos pesos (o que nós queríamos desde o começo) de uma forma elegante e generalizável para todas as camadas.
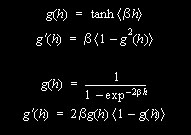

Aprendizado para Redes de Várias Camadas
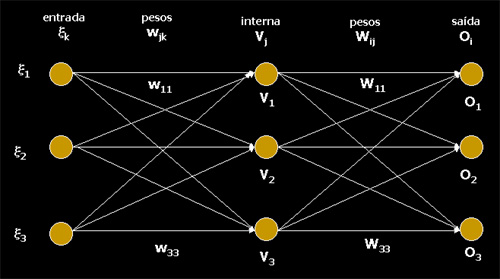
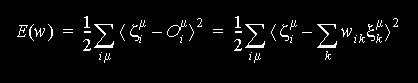





- uma rede feedforward de M camadas
- um conjunto de conexões ponderadas por pesos e dirigidas da camada m-1 para a camada m:
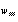
- uma função de ativação não-linear contínua e diferenciável no domínio dos valores a serem treinados na rede
- uma taxa de aprendizado h
- um conjunto de treinamento contendo xm entradas e zm saídas.



3.3.2. O que
Aprende
uma Rede-BP ?
Como citamos em outras partes deste texto, uma rede backpropagation, ao contrário de redes-RBF ou classificadores baseados em Nearest Neighbour, como IBL, aprende uma função capaz de mapear a entrada à saída, caso esta exista. Se o conjunto de treinamento for inconsistente a rede não aprenderá nada ou aprenderá cada exemplo individual do conjunto de treinamento, caso a criemos grande o suficiente.
Em princípio, o mapeamento entrada-saída em uma rede-BP está distribuído sobre o total dos pesos e conexões da rede, sendo bastante difícil associarmos um determinado neurônio e suas conexões a uma determinada classe.
Do ponto de vista matemático, existem várias interpretações do significado dos pesos aprendidos por uma rede neural. Uma discussão detalhada deste assunto foge do escopo de uma disciplina de graduação e nós remetemos à literatura, principalmente [Hertz et.ali.].
Existem, porém, algumas situações interessantes, onde o aprendizado da rede neural pode ser visualizado e podemos realmente associar um ou um conjunto de neurônios a uma determinada classe. Isto tende a acontecer quando o conjunto de treinamento contém classes realmente muito bem comportadas.
O exemplo clássico para este comportamento é o encoder (codificador). Este exemplo está incluído na coleção de exemplo sprontos do SNNS e sugerimos ao leitor que faça alguns experimentos com ele. O encoder é um exemplo onde podemos fazer os padrões de ativação dos neurônios da camada interna representarem uma compressão dos dados de treinamento e ainda utilizar esta compressão de dados como um código representando os mesmos.
O encoder toma um valor de entrada de 0 a 7 e aprende a asociá-lo a mesma saída, possuíndo 8 neurônios de entrada, um para cada valor e 8 neurônios de saída, com a mesma representação. Na camada intermediária possui apenas 3 neurônios. O objetivo é que, ao aprender a associação entrada-saída, ele codifique os dados. A figura abaixo mostra o encoder recebendo o número 1 como padrão de entrada (01000000) e representando internamente este número como 101.
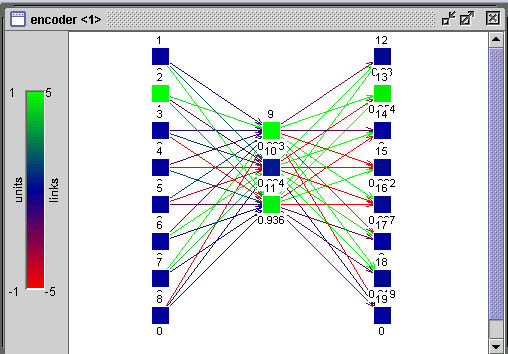
O conjunto de treinamento do encoder não é só linearmente separável, mas é também linearmente independente e, portanto, um conjunto extremamente fácil de aprender, que não necessitaria de uma camada interna, podendo ser representado por um perceptron simples. Mesmo assim é interessante de se observar o fenômeno da representação interna. Este fenômeno porém não ocorre sempre dessa forma, com a rede “inventando” seu próprio código binário. Às vezes os pesos se distribuem de uma forma tal na rede que não é possível uma interpretação visual da “representação interna”.
Exercício: Observando o Encoder
Vamos ver com que freqüência o encoder realmente aprende uma representação interna que para nós, humanos, faz “sentido”. Carregue o exemplo do encoder no SNNS. Reinicialize a rede e treine-o. Bastam 100 épocas pois o conjunto é aprendido extremamente rápido. Feito isto, vá para o modo “updating” e repasse todo o conjunto de treinamento pela rede. Foi possível criar-se um arepresnetação interna similar a algum código binário conhecido ? Repita este processo várias vezes, reincializando, treinando e testando a rede para ver como ela se comporta.
3.3.3. Aspectos Práticos de Métodos de Descida em Gradiente
Como citamos
brevemente antes,
o processo de redução do erro E(w) pertence a uma
categoria
de métodos matemáticos denominado Métodos de
Descida
em Gradiente (Gradient Descent Methods). Nocaso específico das
redes-BP,
que nos interessa, podemos imaginar a idéia de que o erro
é
uma (hiper) superfície em um espaço definido pelos pesos
[w] da rede neural. O estado atual da rede (conjunto de valores
específico
dos pesos das conexões entre os neurônios) é um
ponto
sobre esta superfície. O nosso objetivo é mover este
ponto
através da alteração dos valores do spesos de
forma
a encontrar uma posição onde o erro seja o menor
possível.
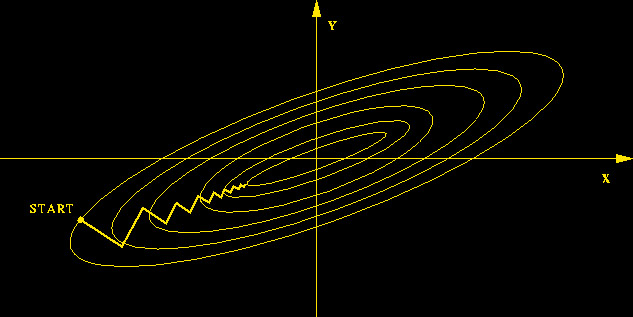
O movimento é realizado sempre no sentido de reduzir-se o erro,
ou seja sempre descendo a superfície de erro de forma que o
próximo
ponto seja uma posição mais funda nesta
superfície,
até encontrar uma posição de onde não sejja
possível descer-se mais. Se imaginarmos uma
situação
3D, onde há apenas dois pesos definindo os espaços x e Y
e a coordenada z sendo definida pelo erro, podemos imaginar o processo
como o mostra a figura abaixo.
O material abaixo
é
um resumo do tutorial
de redes neurais disponibilizado pela Neuro-Fuzzy
AG (Grupo de Trabalho Neuro-Fuzzy) do Departamento de
Matemática
da Universidade de Muenster, Alemanha.
| Mínimo Local: Partindo-se da configuração de pesos inicial w1, o método de descida em gradiente não encontrará a solução (mínimo global). | 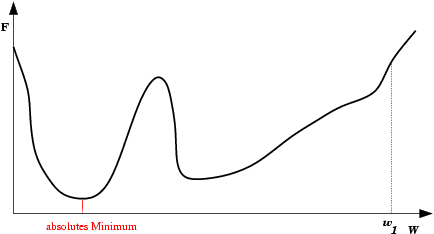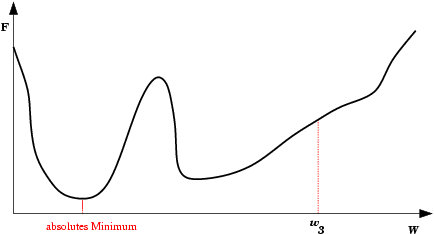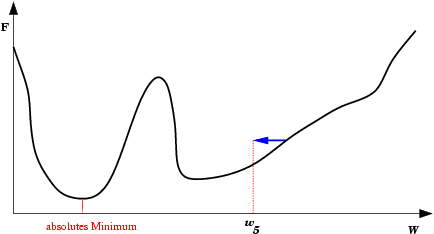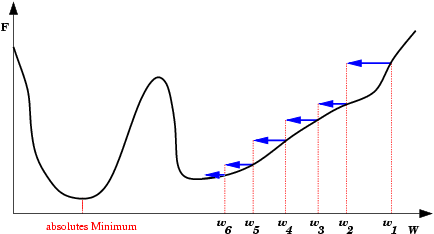 |
| Platô encontrado em E(w) durante treinamento da rede neural. Durante um longo período não haverá mudanças significativas em E(w). Após um tempo, porém, o mínimo absoluto (global) é encontrado. | 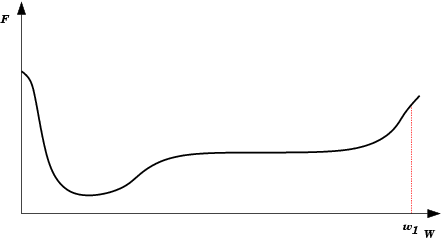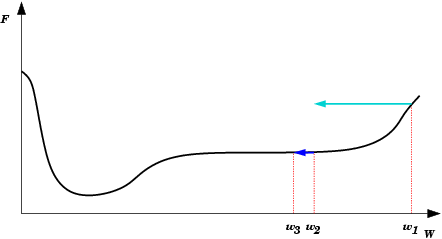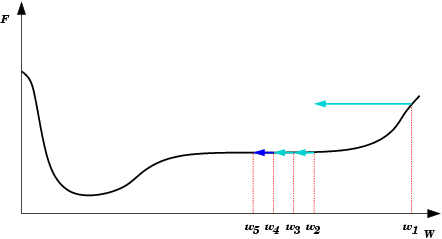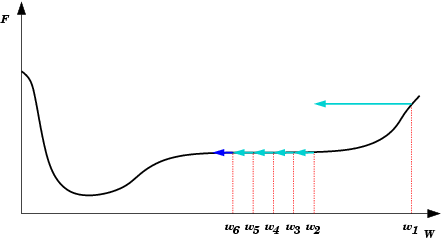 |
| Oscilações ocorrem quando o processo de descida de gradiente cai em uma ravina de onde não sai mais. Também é uma espécie de mínimo local. O passo de modificação dos pesos (taxa de aprendizado) é grande demais para que a rede caia na ravina, mas pequena demais para sair do mínimo. Ao conrário do mínimo local comum, aqui a rede não encontra um estado estável. | 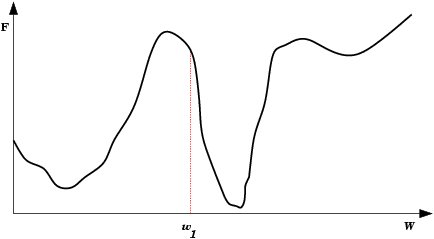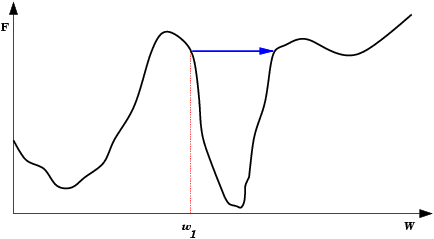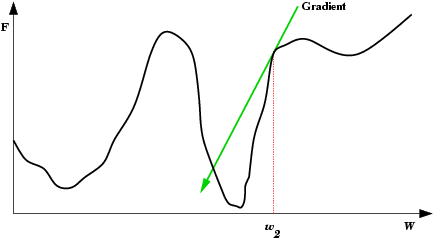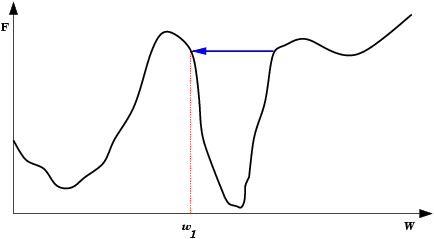 |
| A Oscilação Indireta é uma situação de oscilação mais complexa, onde a rede também fica "presa" em um mínimo local e não encontra um estado estável. Neste caso porém, existem estados intermediários entre os estados extremos da oscilação, onde o erro por momentos se permite reduzir. | 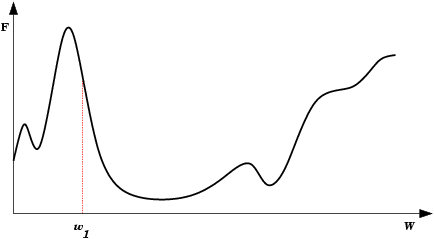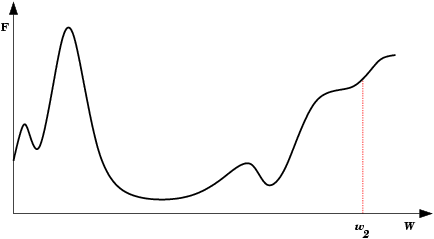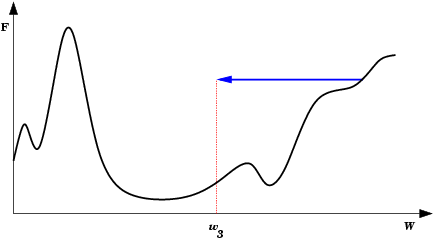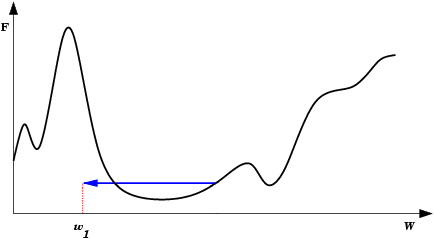 |
| Saída do mínimo ótimo para um subótimo. Se a mudança dos pesos se inicia numa área de gradiente muito grande, os primeiros ajustes podem ser excessivamente grandes e levar a rede a passar do vale onde está o mínimo global, para uma região com um mínimo local. | 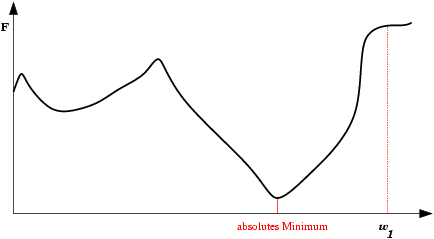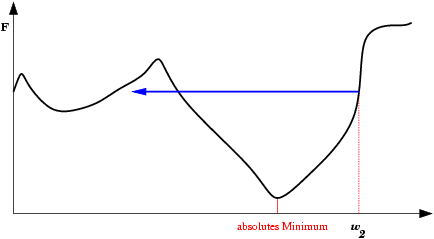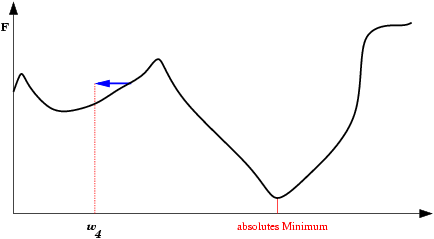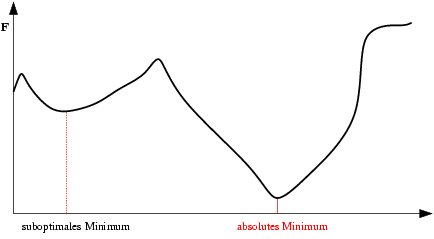 |
Existem
várias técnicas
para "turbinar"a descida em gradiente de forma e evitar alguns dos
problemas
descritos acima. Estas técnicas são implementadas em
parte
no SNNS. Na aula vamos discutir suas vantagens e
limitações.
3.4. Desenvolvimento de Aplicações Usando Aprendizado Supervisionado