2D DFT from 1D DFT

[Laboratory]

The 2D Discrete Fourier Transform is given by the equation:

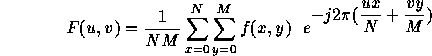
Which can be written as:

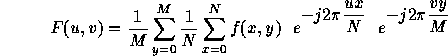
Since the kernel is separable, resulting in:

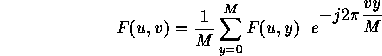
This important result implies that the 2D DFT F(u,v) can be obtained by

1. taking the 1D DFT of every row of image f(x,y), F(u,y),
2. take the 1D DFT of every column of F(u,y)

a)f(x,y); b)F(u,y); c)F(u,v)

a)	b)	c)

The same separable form also applies for the inverse 2D DFT.

Keeping in mind that the 2D DFT can be decomposed using the 1D DFT as a primitive, we can demonstrate most of 2D Discrete Fourier Transform concepts and properties using equations related to 1D DFT.

• Lab: 2D DFT from 1D DFT