

Generation of synthetic data sets, 1D signals and 2D images, are essential for the creation of test patterns, color maps, filter kernels, etc. In this experiment we want to create simple 1D signals and 2D images.

The digital impulse delta(i), also called digital delta function is defined as:
delta(i) = 1, for i = 0
= 0, for other values of i

A sequence of impulses can be built from a summation of several impulses placed at different locations.
![]()
![]()
|
|---|

The equation of a 2D impulses is given by
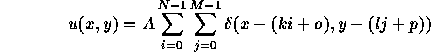
![]()
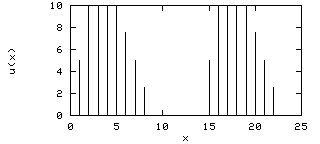
Depicted below is an image with size W=128 and H=100 consisting of 2D impulses. In the width direction there are (N=4) impulses separated by (k=32) pixels, and in the height direction (M=8) impulses separated by (l=10) pixels. The amplitude of each impulse is (A=255). The offsets for both width and height are (o=p=0).

|
|---|

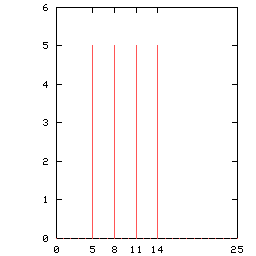
There are several parameters that define a 1D-trapezoidal pulse. min and max are the minimum and maximum values. Other parameters are Rise duration (r), pulse Width (w), Fall duration (f) and pulse Period (t), where each control the length of each part of the pulse. Sampling (sampl) controls the number of samples. For most applications, ilt is easier to use sampl=1.
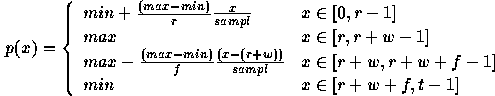
A sequence of almost two trapezoidal pulses, p(x), is shown below:
|
|---|
A particular cases of this function are the square wave (r=f=0), triangular wave (r=f, w=0) and ramp (w=f=0, r=t).
The images shown below correspond to a ramp, triangle and square waves in the width direction. The size of all three images is W=512, H=50 and sampl=1.

|
|---|

|
|---|

|
|---|