Parte II:
Técnicas de Projeto de Algoritmos
Para a maioria dos problemas, as técnicas simples de Análise Estruturada ou de Análise Orientada a Objetos aliadas a um pouco de bom senso e conhecimentos sobre Estruturas de Dados são suficientes para que nós possamos elaborar um algoritmo para resolver este problema.
Exemplos:
Existem alguns problemas porém, onde o caminho a ser seguido para a solução não é tão direto. São problemas onde os algoritmos para resolvê-los ou parte deles não são tão óbvios.
Estes são problemas, onde nós temos de aplicar Técnicas de Projeto de Algoritmos mais elaboradas para resolvê-los.
Exemplos:
Para a solução de problemas assim, existem conjuntos de técnicas que dividem os problemas em classes a apresentam linhas gerais para o projeto de um algoritmo.
Alguns problemas podem ser resolvidos pela técnica "gulosa": A cada ponto, onde temos de tomar um a decisão, tomamos aquela que nos parece ser a melhor neste momento, sem analisar se ela vai ou não nos prejudicar no futuro (caminho do menor esforço).
É a técnica de utilizar a optimalidade local para resolver o problema: Observando o problema como um todo, a cada ponto onde uma decisão é tomada, temos um estado do problema. A técnica "gulosa" consiste em só observarmos o contexto "local" deste estado para escolhermos o próximo estado.
Dois exemplos típicos de algoritmos gulosos são os algoritmos para a Árvore Expandida de Custo Mínimo de Kruskal de de Dijkstra. Em ambos os algoritmos, escolhemos o próximo vértice somente pelo critério "qual é o vértice livre que está mais próximo ?". Um exemplo desses algoritmos voce encontra aqui.
Eu posso representar um problema através de uma tupla <a, b, c..., n> consistindo de todas as variáveis do problema e de um conjunto possível de estados (espaço de estados) representando todos os valores possíveis deste conjunto de variáveis. A idéia da técnica gulosa é resolver o problema sempre aplicando o algoritmos de solução de maneira a tentar ir para um estado de menor valor (ou custo) possível.
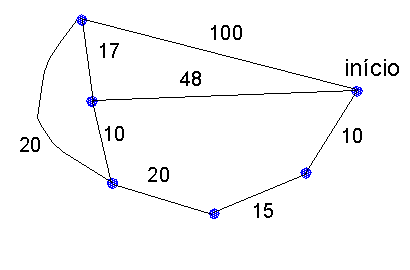
Nem sempre a optimalidade local serve para resolver um problema. No caso do problema do caixeiro viajante e do grafo abaixo, se nós utilizarmos a estratégia de irmos sempre para a cidade mais próxima, nós não vamos encontrar uma solução boa
.
Característica da Técnica Gulosa:
Muitos problemas podem ser resolvidos na sua forma mais "branda" utilizando-se uma técnica gulosa, a solução ótima absoluta, porém, não é garantida.
Exemplo: Distribuição (scheduling) de tempo de trabalho entre processadores:
Implemente o Scheduler acima para a situação de uma empresa têxtil que possue 3 máquinas de bordar desenhos em camisetas usando 3 diferentes técnicas de implementação: a) acaso, b) alg. guloso e c) busca exaustiva antes de iniciar. O tempo para bordar uma camiseta depende do tamanho da camiseta e do tipo do desenho. Esse tempo varia de 10 a 50 segundos.
Teste o tempo final, o tempo médio e o gasto de energia elétrica que essa empresa levaria/teria para bordar um lote de: 6, 9, 18, 30 e 50 camisetas usando a técnica a, b e c. Suponha os tempos em cada lote distribuídos aleatoriamente com uma distribuição uniforme no intervalo 10-50s.
Quais são as suas conclusões ?