INE 5443

Programa

Links

Bibliografia

Plano de Ensino

---

1.1. O que são padrões ? 

1.2. Como montamos um padrão ? 

Assunto ministrado como aula expositiva ao quadro.

1.3. Sinais X Padrões, Exemplos de Sinais e Aplicações.

Assunto ministrado como aula expositiva ao quadro.

1.4. Quais as atividades que realizamos com padrões ?

1.5. Medidas de distância entre padrões: a distância de Hamming, Nearest Neighbour e outras

1.6. Como trabalhamos com padrões usando medidas de distância simples

1.7. Tesselação: Trangulação de Delaunay e o Diagrama de Voronoi

1.7.1. O que é um  Diagrama de Voronoi ?

O Diagrama de Voronoi foi inventado para resolver um problema simples: Como dividir uma cidade em áreas irregulares de forma a que a área coberta por um carteiro vinculado a uma determinada agência de correio seja otimizada ?

G. F. Voronoi, em sua tese de outorado entitulada Ob odnom obobshchenii algorifma nepreryvnykh drobei (Isto é russo para Sobre uma generalização do algoritmo de quebra de cadeias. A transliteração do cirílico é de http://www.algebra.at/voron_d.htm), publicada em Russo em Varsóvia, Polônia, em 1896, desenvolveu um método onde, com base em uma triangulação préexistente de pontos que representam os centros de alguma coisa (no caso da primeira aplicação, agências de correio), se determina qual a área de influência de cada um destes centros em função da posição dos outros centros, delimitando de forma geométrica cada área de influência. 

Abaixo um exemplo encontrado em vários sites na WWW mostrando o problema da distribuição da área de influência dos McDonalds do centro de San Francisco, CA., segundo Th.Ottmann.

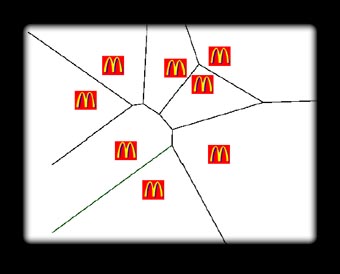
O diagrama de Voronoi é um  método que tem extrema utilidade em reconhecimento de padrões para delimitar as áreas de categorias ou classes em uma representação geométrica de suas distribuições.

Chamamos estes "centros" de centróides. Se nós temos um conjunto de padrões constituído de um elemento típico para cada categoria que queremos representar (protótipo), podemos nos utilizar do diagrama de Voronoi para determinar a extensão de cada uma das categorias, simplesmente utilizando cada um dos protótipos como um centróide e gerando um diagrama de Voronoi sobre estes. 

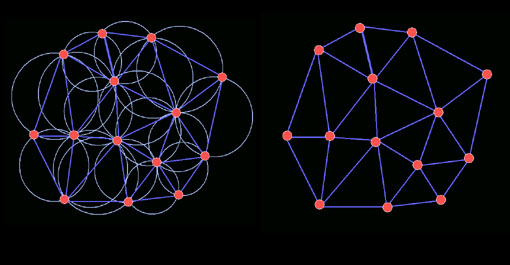
Para podermos gerar um diagrama de Voronoi partimos do conjunto de protótipos e geramos primeiramente uma triangulação. Para isto utilizamos o método da Triangulação de Delaunay, que veremos em detalhe adiante. Na figura abaixo, a triangulação está em vermelho.

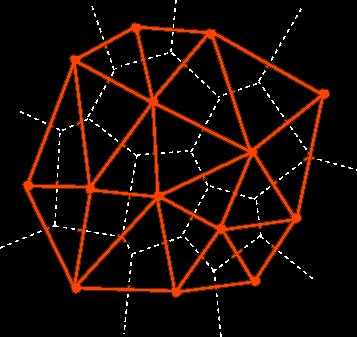
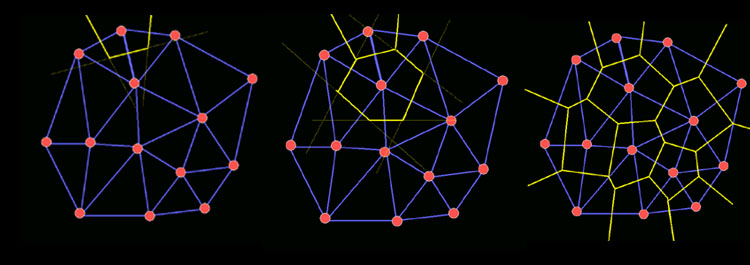
Realizada a triangulação, geramos as linhas que formarão as fronteiras das células do diagrama de Voronoi. Estas fronteiras são geradas por linhas perpendiculares ao ponto médio de cada aresta da triangulação produzida anteriormente. As intersecções destas perpendiculares formam os vértices das células do diagrama de Voronoi. Os segmentos de reta da perpendicular que se extendem para além de sua primeira intersecção com outra perpendicular nos dois sentidos são descartados.

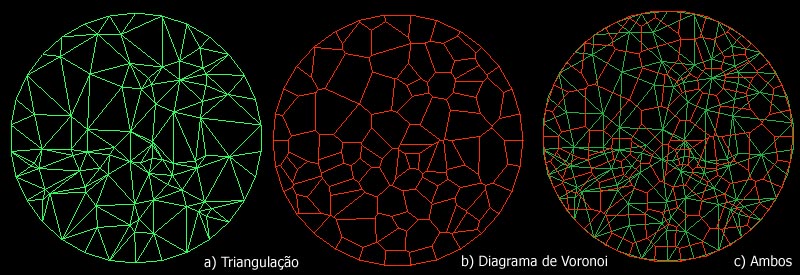
Na figura acima vemos em (a) uma triangulação inicial, em (b) o diagrama de Voronoi resultante e em (c) ambos sobrepostos. 

1.7.2. Passos para a geração de um Diagrama de Voronoi

O algoritmo que descreveremos a aseguir é uma descrição de alto nível dos passos necessários para a geração de um diagrama de Voronoi para uma distribuição qualquer de dados sobre um plano. O método pressupõe que a distribuição de dados é bidimensional, sendo um caso particular do modelo geral. Se desejarmso mapear uma distribuição de dados de dimensão maior ou igual a 3 temos de utilizar planos e não segmentos de reta como fornteiras e cada elemento da triangulação será representado por um volume com n+1 faces, onde n é a dimensionalidade dos dados. Assim, por exemplo, paar representar dados em 3D através de um diagrama de Voronoi teremos de utilizar tetraedros (4 faces) como estrutura de triangulação. 

Passo 1: Determinação dos pontos para os triangulos (Triangulação de Delaunay)

Tome sua distribuição de dados e encontre todos os triângulos definidos por três pontos da distribuição, de tal forma que um círculo passando por estes três pontos não inclua nenhum outro ponto.

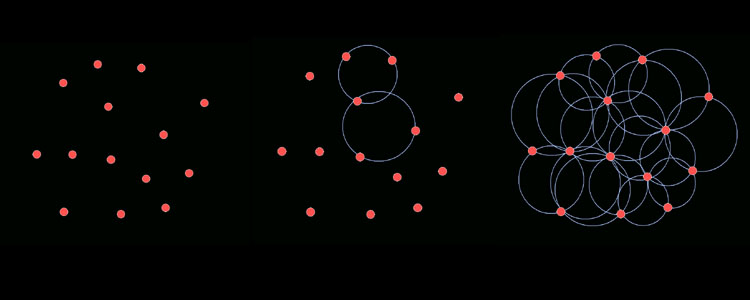
Passo 2: Determinação dos triangulos (Triangulação de Delaunay)

Para cada conjunto de três pontos satisfazendo a condição de Delaunay encontrado, gere um triângulo.

P.3.1. Determine o ponto médio de cada um adas arestas do conjunto de triângulos gerado anteriormente. Considere cada aresta apenas uma vez. 
P.3.2. Gere uma linha perpendicular a cada uma das arestas.
P.3.3. Determine as duas intersecções mais próximas de cada aresta com duas outras arestas. Um intersecção para cada lado. Ignore os segmentos de reta que seguem para além das intersecções.
P.3.4. Forme as células do diagrama com os polgonos formados por segmentos adjacentes. Ciclos geram células internas, polígonos abertos células externas.

1.8. Exercícios

Os conjuntos de dados em espiral podem ser utilizados para testes de performance em algoritmos de classificação de dados pois podem ser gerados automaticamente com variados graus de detalhes e ruído. 

1.8.1.1. A espiral simples

Neste caso temos dados distribuídos em espiral em 2D. Cada ponto representa o protótipo de um acategoria ou classe. A tarefa de reconhecimento de padrões é classificá-los adequadamente, de forma a associar outros dados aleatórios a uma das classes existente na espiral. 

Você pode gerar uma espiral simples você mesmo através de um algoritmo operando em coordenadas polares com passo constante e raio reduzindo-se linearmente.

1.8.1.2. A espiral dupla

As espirais múltiplas consituem um problema diferente da espiral simples. Em uma espiral múltipla, cada braço da espiral representa uma categoria ou classe. Cada classe é representada por muitos pontos, que são organizados sob forma de espiral. A tarefa aqui é classificar um ponto aleatório como pertencente a uma determinada classe, representada através de um braço da espiral.

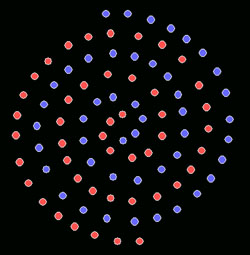
Uma solução para evitar o uso de um enfoque não-linear para gerar um classificador para este conjunto de dados (como por exemplo uma rede neural bastante grande baseada em preceptrons mas utilizando o algoritmo Backpropagation de Rummelhart e McLelland) é gerar-se um classificador parcialmente linear (piecewise linear). Isto pode ser obtido, por exemplo através de comparação através de Nearest Neighbour com todos os dados da espiral. Nearest Neighbour é um classificador linear, mas se o usamos passo a passo com todos os elementos da espiral vamos descobrir uma classificação ótima para um dado aleatório. Outra opção (que no fundo é bastante similar nas suas bases) é considerar cada elemtno dos dois conjuntos de dados como um centroide e gerar-se um diagrama de Voronoi para a espiral dupla. Depois classifica-se cada uma das células como pertencendo à categoria vermelha ou azul, de acordo com a categoria de seu centroide.

A figura acima mostra as duas superfícies de decisão de  uma espiral de dois braços aprendido através de um modelo de rede neural denominado SEN3 (Self-Editing Nearest Neighbor Net - Rahmel & v.Wangenheim, 1994) com base em um conjunto de dados de uma espiral de dois braços contendo ruído. Observe que a geração das duas superfícies de decisão nã é perfeita. A rede SEN3  é inspirada no modelo de Kohonen e utiliza Nearest Neighbour como parte de sua regra de aprendizado.

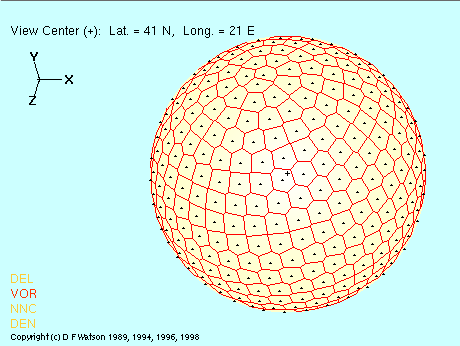
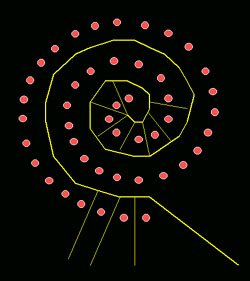
A figura acima mostra um diagrama de Voronoi gerado para um conjunto de dados em espiral situados sobre a superfície de uma esfera.

1.8.2. Exercícios para entregar
 

1. Prepare 4 conjuntos de dados: 2 conjuntos de dados qauisquer (um deles em 2D (duas variáveis apenas) e outro nD (com um grande numero de variáveis)) e dois conjuntos de dados espirais (um deles espiral simples e outro espiral de dois braços)
1. Ex.: os dados 2D e nD podem ser utilizados a partir de conjunos de dados disponíveis nos sites sugeridos.
2. Os dados em espiral devem ser gerados a partir de algoritmos que você mesmo vai implementar. Inclua no algoritmo a possibilidade de introduzir ruído na geração dos dados (através de uma variável aleatório que modifica levemente o comprimento do raio gerado para o próximo ponto).
2. Implemente a Distância de Hamming, NN (Nearest Neighbour) e kNN (k-Nearest Neighbours) e teste em todos os 4 conjuntos de dados. Observe que na espiral dupla, cada braço da espiral em seu total representa uma classe. Ilemente um programa de teste de tal forma que nos casos 2D e espiral dupla os dados sejam plotados de forma colorida (duas cores para os dados originais e outras duas cores para o resultado de classificação dos dados). Dessa forma pode-se visualizar onde estão os dados que definem as classes e também onde estão pontos gerados para teste e como foram classificados. No caso da espiral simples utiliza cores alternadas, já que cada ponto representa uma classe por si.
3. Implemente o Diagrama de Voronoi e teste nos Dados 2D e nas duas espirais.

1.9. Links Úteis e Interesasantes sobre o Assunto

• Directory of Computational Geometry Software
• Arbitrary dimensional convex hull, Voronoi diagram, Delaunay triangulation
• Triangulation
• Voronoi Diagrams: http://www.ics.uci.edu/~eppstein/gina/voronoi.html
• The Voronoi Web Site
• ftp://geom.umn.edu/
• Demo: http://members.iinet.net.au/~watson/mm_applet.html

The Cyclops Project German-Brazilian Cooperation Programme on IT CNPq GMD DLR