INE 5443
5. Técnicas Estatísticas
5.1. Introdução
às Técnicas Estatísticas Exploratórias: Estatística
Multivariada
5.2. Análise
de Discriminantes
5.3. Análise
de Agrupamentos
5.4. Visão
Geral das demais Técnicas Multivariadas
5.5. Glossário
de Termos Estatísticos
5.6. Links
Úteis
 5.1. Introdução às Técnicas
Estatísticas
Exploratórias: Estatística Multivariada
5.1. Introdução às Técnicas
Estatísticas
Exploratórias: Estatística Multivariada
Do ponto de vista da
Estatística,
as técnicas úteis para reconhecimento e descoberta de
padrões
em ambientes onde os fenômenos são descritos/baseados em
uma
grande variedade de dados são conhecidas como Análise de
Dados Exploratória (ADE) ou Estatística
Exploratória.
A Análise de Dados Exploratória está relacionada de forma próxima com o conceito de Mineração de Dados. De um ponto de vista das técnicas estatísticas, ao contrário dos testes de hipóteses tradicionais, projetados para verificar uma hipótese a priori acerca de relacionamentos entre variáveis ( "Existe uma correlação positiva entre a IDADE de uma pessoa e o NÍVEL DE VIOLÊNCIA dos filmes locados em uma locadora?"), a Análise de Dados Exploratória é utilizada para a identificação de relacionamentos sistemáticos entre variáveis quando não existem expectativas a priori acerca da natureza destes relacionamentos ou estas são incompletas. Em um processo de ADE típico, muitas variáveis diferentes são consideradas e comparadas. Isto é realizado utilizando-se uma grande variedade de técnicas e modelos matemáticos com o objetivo de se encontrar padrões nestes dados.
O que é um conjunto de dados multivariado?
Até agora, na Disciplina de RP, nos ocupamos com métodos e técnicas para trabalhar com conjuntos de dados multivariados, sem nos preocupar muito com essa nomenclatura. Um conjunto de dados multivariado é um conjunto de dados onde cada caso ou observação de um fenômeno é descrito por um conjunto de várias variáveis, sendo representado tipicamente por um padrão (n+1)-dimensional, onde n>2 é número de variáveis necessárias para descrever o fenômeno ou observação e a variável n+1 descreve a classe à qual este determinado padrão pertence.
No mundo da Estatística, porém, faz-se uma diferenciação rigorosa se um fenômeno é baseado em uma, duas ou muitas variáveis (mono-, bi- ou multivariado), pois as técnicas estatísticas utilizadas para cada um desses três casos variam muito e são tratadas separadamente.
Como aplicamos ADE ao Reconhecimento de Padrões?
Podemos aplicar a ADE ao reconhecimento de padrões de duas formas diferentes:
- Por um lado, as técnicas de ADE já são em si técnicas de reconhecimento de padrões, já que são projetadas para detectar regularidades, correlações e fatores agrupadores ou diferenciadores em um conjunto de dados. Sob esta ótica, realizar mineração de dados com ADEs ou aplicar ADEs a um problema já é uma forma de realizar reconhecimento de padrões. A aplicação prática das técnicas de ADE em RP sob esta ótica dispensa maiores explicações; basta que aprendamos as técnicas.
- Por outro lado, podemos utilizar técnicas da ADE como ferramentas para a extração de informações de conjuntos de dados com o objetivo de utilizar estas informações para a implementação de um classificador. Neste enfoque, o desenvolvimento completo de uma solução envolve mais do que as técnicas de ADE em si, pois exige que se utilize ainda outra técnica adicional para a implementação deste classificador. Esta idéia vamos detalhar um pouco mais nos parágrafos abaixo.
O resultado dessa análise inicial através de técnicas exploratórias pode nos prover dados para a elaboração de um mecanismo de classificação utilizando técnicas tradicionais, como k-NN ou outras de RP, através de informações sobre distribuições de dados ou variáveis-chave para classificação dos dados em classes. Em casos onde não conhecemos a priori em quais e quantas classes os dados se permitem agrupar, pode-se inclusive determinar estas classes e utilizar esta informação para um posterior mecanismo de classificação.
A utilização de técnicas estatísticas para o desenvolvimento de classificadores em Reconhecimento de Padrões é, portanto, baseada em uma filosofia de dois passos:
- Primeiramente escolhemos uma técnica da ADE para gerar um conjunto de informações a partir de um conjunto inicial de dados gerado por um processo que desejamos dominar capaz de servir para utilização em um classificador e subseqüentemente ser utilizado para a classificação de novos casos gerados pelo mesmo processo que gerou os dados originais;
- Escolhemos uma técnica de RP adequada ao tipo de informação gerada pelo método de ADE utilizado e também adequada ao tipo de classificação que queremos obter para dados futuros e utilizamos a informação gerada pela ADE para alimentar ou implementar o classificador.
Podemos dividir as técnicas de ADE em dois grupos. Algumas técnicas de ADE são baseadas em estatísticas bastante simples, outras, denominadas Técnicas Exploratórias Multivariadas, foram projetadas para identificar padrões em conjuntos de dados multivariados.
- Métodos Estatísticos Exploratórios Básicos. São técnicas para analisar a distribuição de variáveis, verificar matrizes de correlação para encontrar coeficientes acima de determinados limiares ou examinar tabelas de freqüência multivias. São ferramentas matemáticas interessantes e são utilizadas como componentes em técnicas estatísticas mais complexas, mas não podem ser consideradas técnicas de Reconhecimento de Padrões.
- Técnicas Exploratórias Multivariadas. Técnicas projetadas especificamente para identificar padrões em conjuntos de dados multivariados ou conjuntos de dados univariados representando seqüências de observações ou mensurações de um fenômeno.
- Análise de Correspondências (Correspondence Analysis),
- Análise de Agrupamentos (Cluster Analysis),
- Análise Fatorial (Factor Analysis),
- Análise de Discriminantes (Discriminant Function Analysis),
- Escalonamento Multidimensional (Multidimensional Scaling),
- Análise Log-Linear (Log-linear Analysis),
- Correlação Canônica (Canonical Correlation),
- Regressão Parcialmente Linear e Não-Linear (Stepwise Linear and Nonlinear Regression),
- Análise de Séries Temporais (Time Series Analysis),
- Árvores de Classificação/Decisão (Classification Trees).
As técnicas multivariadas são comumente divididas em:
Alguns autores ainda classificam as Redes Neurais como técnicas da Análise de Dados Exploratória. Nós pessoalmente consideramos que a ADE é um campo da Estatística e deveria conter apenas Métodos Estatísticos formalmente definidos como tais.
Assuntos na Disciplina
No correr desta disciplina vamos analisar em detalhes duas técnicas multivariadas da Estatística Exploratória (EDA) que são de maior interesse para a utilização para o desenvolvimento de classificadores:
- Análise de Discriminantes e
- Análise de Agrupamentos
Trabalhos Práticos na Disciplina e Softwares Estatísticos
Hoje em dia existem vários softwares estatísticos que oferecem os métodos multivariados que veremos ao longo desta disciplina. Como o objetivo da disciplina na área de ADE é que você aprenda a utilizar as técnicas e não que você as implemente, diferentemente do que foi nossa filosofia em outros tópicos de RP em capítulos passados, nós vamos nos utilizar de implementações prontas dos métodos de ADE. Os trabalhos práticos poderão ser realizados através da utilização de qualquer ferramenta de software estatístico. Dentre as muitas implementações que existem, destacamos duas:
SPSS - Um dos mais antigos pacotes de software estatístico existentes e utilizado como ferramenta de referência em muitas áreas das Ciências Biológicas e da Saúde (em meu tempo de graduação já utilizávamos SPSS em mainframes IBM sob VM 370).Ambos os pacotes possuem em suas páginas demos ou trials para download (Download do Trial do SPSS, Download do Trial do Statistica), que são suficientes para a realização de muitas das atividades nesta disciplina (o demo do Statistica não possui algumas funcionalidades). Sugerimos que você baixe ambos e compare-os, escolhendo um deles como ferramenta para a realização de seus trabalhos. Na seção de links ao final desta página estão ainda disponibilizados vários sites que contém software livre para ADE. Nós ainda não testamos nenhum destes pacotes de software e encorajamos você a que investigue as possibilidades oferecidas por estes pacotes gratuitos.
Statistica - Talvez o mais moderno e mais completo pacote na área. Muitos pesquisadores consideram o Statistica como a melhor ferramenta estatística existente. O Statistica é muito completo e possui muito material de apoio, além de helpfiles extremamente bem estruturados e escritos. Muitos dos exemplos que utilizaremos ao longo deste capítulo são adaptações de exemplos encontrados nos helpfiles do Statistica.
 5.2. Análise de Discriminantes
5.2. Análise de Discriminantes
A análise estatística multivariada utilizando funções discriminantes foi inicialmente aplicada para decidir à qual de dois grupos pertenceriam indivíduos sobre os quais tinham sido feitas diversas e idênticas mensurações. Nessa análise, hoje conhecida como análise discriminante linear, a idéia básica é substituir o conjunto original das diversas mensurações por um único valor Di, definido como uma combinação linear delas. Quando se trata de discriminar entre mais de dois grupos torna-se necessário uma generalização na metodologia. A análise discriminante multigrupos, que utiliza procedimentos combinados da análise de variância e da análise fatorial, pode, então, ser utilizada.
5.2.1. Exemplos de aplicação de análise discriminante
Exemplo 1: Clientes de uma empresa (2 grupos):- Análise de Discriminantes: Como selecionar variáveis que melhor discriminam clientes que permanecem e clientes que abandonam os serviços da empresa?
- Construção de regras de classificação: Conhecidos os valores das variáveis de um novo cliente, classificá-lo no grupo dos que abandonam ou no grupo dos que permanecem na empresa.
- Análise de Discriminantes: Como selecionar variáveis que melhor discriminam clientes que pagam e clientes que não pagam seus débitos?
- Construção de regras de classificação: Conhecidos os valores das variáveis de um novo cliente, classificá-lo no grupo dos que pagam ou no grupo dos que não pagam.
(1) ir para a universidade,Para esse fim o pesquisador poderia coletar um grande número de variáveis a respeito da vida do estudante antes de sua formatura no ensino médio. Após a formatura no ensino médio, a esmagadora maioria dos estudantes cairá em uma das três categorias acima. A Análise de Discirminantes Multigrupos pode então ser utilizada para determinar quais variáveis melhor predizem qual será a escolha educacional do indivíduo após o término do ensino médio.
(2) fazer algum tipo de ensino técnico ou profissionalizante ou
(3) não procurar nenhum tipo de educação adicional.
Exemplo 4: Prognóstico de recuperação (3 grupos -> análise discriminante multigrupos): Um pesquisador médico pode ter registrado um conjunto de diferentes variáveis relacionadas aos backgrounds de seus pacientes com o objetivo de descobrir retrospectivamente quais variáveis melhor predizem se um paciente tem chances de:
(1) recuperar-se completamente da doença,Exemplo 5: Discriminação entre espécies (n grupos -> análise discriminante multigrupos): Um biólogo pode ter registrado as várias características de tipos ou espécies muito similares (grupos) de flores. A seguir ele poderá executar uma análise de discriminantes para determinar quais características oferecem a melhor discriminação entre as espécies. Esta aplicação está descrita abaixo no Segundo Exemplo Detalhado: Discriminando Diferentes Variedades de Iris.
(2) recuperar-se parcialmente da doença, mantendo algumas seqüelas, ou
(3) não se recuperar de maneira alguma.
5.2.2. Objetivos da Análise de Discriminantes
Do ponto de vista computacional, a Análise de Discriminantes é muito similar à Análise de Variância (ANOVA). Para entender isto, vamos ver um exemplo simples: suponha que nós meçamos a altura em uma amostra aleatória de 50 homens e 50 mulheres. As mulheres são, em sua média, menos altas que os homens e esta diferença será refletida pela diferença nas médias entre as variáveis altura de ambos os grupos.Em função disso, a variável altura nos permite discriminar entre homens e mulheres com uma probabilidade melhor do que o puro acaso (na nossa amostra, a probabilidade de alguém escolhido ao acaso ser homem é de 50%; a probabilidade de alguém escolhido ao acaso, se for alto, ser homem é maior): se uma pessoa for alta, ela será mais provavelmente um homem do que uma mulher.
Podemos generalizar esta idéia para variáveis menos triviais. Imagine um estudo similar ao exemplo 3, onde queremos saber quais as razões por que formandos do ensino médio escolhem ou não fazer um curso universitário. Poderíamos simplesmente ter medido, por exemplo, a intenção alegada pelos estudantes de seguir estudos universitários ou não um ano antes da formatura no ensino médio. Se as médias para os dois grupos (aqueles que de fato prestaram vestibular e aqueles que não o fizeram) são diferentes, então podemos dizer que a intenção alegada um ano antes de fazer ou não um curso universitário nos permite discriminar entre aqueles com interesses universitário ou não. Essa informação poderia então ser utilizada de forma mais objetiva pelos conselheiros pedagógicos em diversas escolas do ensino médio para orientar os estudos dos alunos.
Estruturando o que foi dito acima, queremos:
- Medir o poder de discriminação de cada variável ou grupo de variáveis;
- Descrever graficamente ou algebricamente diferentes grupos em termos de variáveis discriminadoras;
- Desenvolver regras para classificar novos elementos.
Sumarizando o que foi discutido até agora: a idéia básica por trás da análise de discriminantes é determinar se os grupos são diferentes com relação à média de uma variável, e então usar essa variável para prever a que grupo um novo caso pertence.
Dito dessa maneira, o problema da análise de discriminantes pode ser pensado como um problema de análise de variância (ANOVA) de uma via. Especificamente, pode-se perguntar se um ou mais grupos são ou não significativamente diferentes entre si com respeito à média de uma variável em particular.
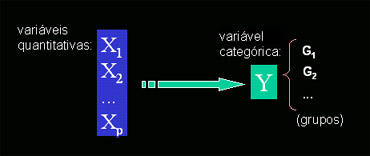
O nosso objetivo é determinar quais variáveis são categóricas, i.e., nos permitem discriminar entre categorias.
Principais Perguntas
Considerando amostras de p variáveis, relativas a elementos de g grupos, como se pode:- verificar as variáveis que discriminam (separam) melhor os grupos?
- medir analiticamente a separação dos grupos?
- visualizar graficamente a separação dos grupos?
- A partir de amostras de p variáveis de elementos de vários grupos, como pode-se criar regras de classificação que permitam classificar novos elementos em um dos grupos?
- Como avaliar a qualidade do processo de classificação?
5.2.3. Primeiro Exemplo Detalhado: Discriminação entre portadores ou não de Hemofilia
Tomemos para isso o seguinte exemplo:Grupo 1: mulheres não portadoras de hemofilia A (normais) (n1 = 30)Os dados são:
Grupo 2: mulheres portadoras de hemofilia A (portadoras) (n2 = 22)
Suponha que as variáveis discriminadoras são: X1 e X2 (duas variáveis contínuas observadas em exames de sangue). No nosso exemplo vamos considerar somente essas.
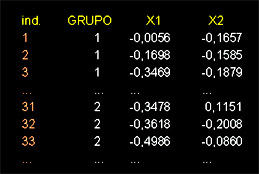
Um scatter plot da distribuição dos dados fica assim:

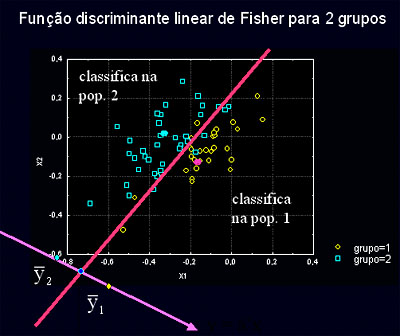
5.2.4. Formas de Análise de Discriminantes
Estime os coeficientes da função discriminante e determine a significância estatística e a validade — escolha o método de análise de discriminantes apropriado.- The direct method involves estimating the discriminant function so that all the predictors are assessed simultaneously. The stepwise method enters the predictors sequentially.
- The two-group method should be used when the dependent variable has two categories or states.
- The multiple discriminant method is used when the dependent variable has three or more categorical states.
5.2.5. Análise de Discriminates sobre uma única Variável
the final significance test of whether or not a variable discriminates between groups is the F test. F is essentially computed as the ratio of the between-groups variance in the data over the pooled (average) within-group variance. If the between-group variance is significantly larger then there must be significant differences between means.5.2.6. Análise de Discriminantes com Múltiplas Variáveis
Usually, one includes several variables in a study in order to see which one(s) contribute to the discrimination between groups. In that case, we have a matrix of total variances and covariances; likewise, we have a matrix of pooled within-group variances and covariances. We can compare those two matrices via multivariate F tests in order to determined whether or not there are any significant differences (with regard to all variables) between groups. This procedure is identical to multivariate analysis of variance or MANOVA. As in MANOVA, one could first perform the multivariate test, and, if statistically significant, proceed to see which of the variables have significantly different means across the groups. Thus, even though the computations with multiple variables are more complex, the principal reasoning still applies, namely, that we are looking for variables that discriminate between groups, as evident in observed mean differences. In fact, you may perform discriminant function analysis with the ANOVA/MANOVA module; however, different types of statistics are customarily computed and interpreted in discriminant analysis (as describedlater).
5.2.7. Pressupostos Fundamentais por Detrás da Análise de Discriminantes
Discriminant function analysis is computationally very similar to MANOVA, and all assumptions for MANOVA mentioned in ANOVA/MANOVA apply. In fact, you can use the wide range of diagnostics and statistical tests of assumption that are available in ANOVA/MANOVA to examine your data for the discriminant analysis (to avoid unnecessary duplications, the extensive set of facilities provided in ANOVA/MANOVA is not repeated in Discriminant Analysis):- Normal distribution. It is assumed that the data (for the variables) represent a sample from a multivariate normal distribution. Note that it is very simple to produce histograms of frequency distributions from within results spreadsheets via the shortcut menu, which allows you to examine whether or not variables are normally distributed. However, note that violations of the normality assumption are usually not "fatal," meaning, that the resultant significance tests etc. are still "trustworthy." ANOVA/MANOVA provides specific tests for normality.
- Homogeneity of variances/covariances. It is assumed that the variance/covariance matrices of variables are homogeneous across groups. Again, minor deviations are not that important; however, before accepting final conclusions for an important study it is probably a good idea to review the within-groups variances and correlation matrices. In particular the scatterplot matrix that can be produced from the Prob. and Scatterplots tab of the Descriptive Statistics dialog can be very useful for this purpose. When in doubt, try re-running the analyses excluding one or two groups that are of less interest. If the overall results (interpretations) hold up, you probably do not have a problem. You may also use the numerous tests and facilities in ANOVA/MANOVA to examine whether or not this assumption is violated in your data. However, as mentioned in ANOVA/MANOVA, the multivariate Box M test for homogeneity of variances/covariances is particularly sensitive to deviations from multivariate normality, and should not be taken too "seriously."
- Correlations between means and variances. The major "real" threat to the validity of significance tests occurs when the means for variables across groups are correlated with the variances (or standard deviations). Intuitively, if there is large variability in a group with particularly high means on some variables, then those high means are not reliable. However, the overall significance tests are based on pooled variances, that is, the average variance across all groups. Thus, the significance tests of the relatively larger means (with the large variances) would be based on the relatively smaller pooled variances, resulting erroneously in statistical significance. In practice, this pattern may occur if one group in the study contains a few extreme outliers, who have a large impact on the means, and also increase the variability. To guard against this problem, inspect the descriptive statistics, that is, the means and standard deviations or variances for such a correlation. ANOVA/MANOVA also allows you to plot the means and variances (or standard deviations) in a scatterplot.
- The matrix ill-conditioning problem. Another assumption of discriminant function analysis is that the variables that are used to discriminate between groups are not completely redundant. As part of the computations involved in discriminant analysis, STATISTICA inverts the variance/covariance matrix of the variables in the model. If any one of the variables is completely redundant with the other variables then the matrix is said to be ill-conditioned, and it cannot be inverted. For example, if a variable is the sum of three other variables that are also in the model, then the matrix is ill-conditioned.
- Tolerance values. In order to guard against matrix ill-conditioning, STATISTICA constantly checks the so-called tolerance value for each variable. This value is also routinely displayed when you ask to review the summary statistics for variables that are in the model, and those that are not in the model. This tolerance value is computed as 1 minus R-square of the respective variable with all other variables included in the current model. Thus, it is the proportion of variance that is unique to the respective variable. You can also refer to Multiple Regression to learn more about multiple regression and the interpretation of the tolerance value. In general, when a variable is almost completely redundant (and, therefore, the matrix ill-conditioning problem is likely to occur), the tolerance value for that variable will approach 0. The default value in Discriminant Analysis for the minimum acceptable tolerance is 0.01. STATISTICA issues a matrix ill-conditioning message when the tolerance for any variable falls below that value, that is if any variable is more than 99% redundant (you may change this default value by selecting the Advanced options (stepwise analysis) check box on the Quick tab of the Discriminant Function Analysis dialog, and then adjusting the Tolerance box on the resulting Advanced tab of the Model Definition dialog).
5.2.8. Análise de Discriminantes do Tipo Passo a Passo
Probably the most common application of discriminant function analysis is to include many measures in the study, in order to determine the ones that discriminate between groups. For example, an educational researcher interested in predicting high school graduates' choices for further education would probably include as many measures of personality, achievement motivation, academic performance, etc. as possible in order to learn which one(s) offer the best prediction.Model. Put another way, we want to build a "model" of how we can best predict to which group a case belongs. In the following discussion we will use the term "in the model" in order to refer to variables that are included in the prediction of group membership, and we will refer to variables as being "not in the model" if they are not included.
Forward stepwise analysis. In stepwise discriminant function analysis, STATISTICA "builds" a model of discrimination step-by-step. Specifically, at each step STATISTICA reviews all variables and evaluate which one will contribute most to the discrimination between groups. That variable will then be included in the model, and STATISTICA proceeds to the next step.
Backward stepwise analysis. You can also step backwards; in that case STATISTICA first includes all variables in the model and then, at each step, eliminates the variable that contributes least to the prediction of group membership. Thus, as the result of a successful discriminant function analysis, one would only keep the "important" variables in the model, that is, those variables that contribute the most to the discrimination between groups.
F to enter, F to remove. The stepwise procedure is "guided" by the respective F to enter and F to remove values. The F value for a variable indicates its statistical significance in the discrimination between groups, that is, it is a measure of the extent to which a variable makes a unique contribution to the prediction of group membership. If you are familiar with stepwise multiple regression procedures (see Multiple Regression), then you may interpret the F to enter/remove values in the same way as in stepwise regression.
In general, STATISTICA continues to choose variables to be included in the model, as long as the respective F values for those variables are larger than the user-specified F to enter; STATISTICA excludes (removes) variables from the model if their significance is less than the user-specified F to remove.
Capitalizing on
chance. A
common misinterpretation of the results of stepwise discriminant
analysis
is to take statistical significance levels at face value. When
STATISTICA
decides which variable to include or exclude in the next step of the
analysis,
it actually computes the significance of the contribution of each
variable
under consideration. Therefore, by nature, the stepwise procedures will
capitalize on chance because they "pick and choose" the variables to be
included in the model so as to yield maximum discrimination. Thus, when
using the stepwise approach you should be aware that the significance
levels
do not reflect the true alpha error rate, that is, the probability of
erroneously
rejecting H0 (the null hypothesis that there is no discrimination
between
groups).
5.2.9. Como Interpretar uma Função Discriminante entre Dois Grupos ?
In the two-group case, discriminant function analysis can also be thought of as (and is analogous to) multiple regression (see Multiple Regression; the two-group discriminant analysis is also called Fisher linear discriminant analysis after Fisher, 1936; computationally all of these approaches are analogous). If we code the two groups in the analysis as 1 and 2, and use that variable as the dependent variable in a multiple regression analysis, then we would get results that are analogous to those we would obtain via Discriminant Analysis. In general, in the two-group case we fit a linear equation of the type:Group = a + b1*x1 + b2*x2 + ... + bm*xm
where a is a
constant and
b1 through bm are regression coefficients. The interpretation of the
results
of a two-group problem is straightforward and closely follows the logic
of multiple regression: Those variables with the largest (standardized)
regression coefficients are the ones that contribute most to the
prediction
of group membership.
5.2.10. Análise de Discrimantes para Determinação de Funções Discriminantes entre Vários Grupos
When there are more than two groups, we can estimate more than one discriminant function like the one presented above. For example, when there are three groups, we could estimate (1) a function for discriminating between group 1 and groups 2 and 3 combined, and (2) another function for discriminating between group 2 and group 3. We could have one function that discriminates between those high school graduates that go to college and those who do not (but rather get a job or go to a professional or trade school), and a second function to discriminate between those graduates that go to a professional or trade school versus those who get a job. The b coefficients in those discriminant functions could then be interpreted as before.- Análise Canônica: When actually performing a multiple group discriminant analysis, we do not have to specify how to combine groups so as to form different discriminant functions. Rather, STATISTICA automatically determines some optimal combination of variables so that the first function provides the most overall discrimination between groups, the second provides second most, and so on. Moreover, the functions will be independent or orthogonal, that is, their contributions to the discrimination between groups will not overlap. Computationally, STATISTICA performs a canonical correlation analysis (see also Canonical Correlation) that will determine the successive functions and canonical roots (the term root refers to the eigenvalues that are associated with the respective canonical function). The maximum number of functions that STATISTICA computes are equal to the number of groups minus one, or the number of variables in the analysis, whichever is smaller.
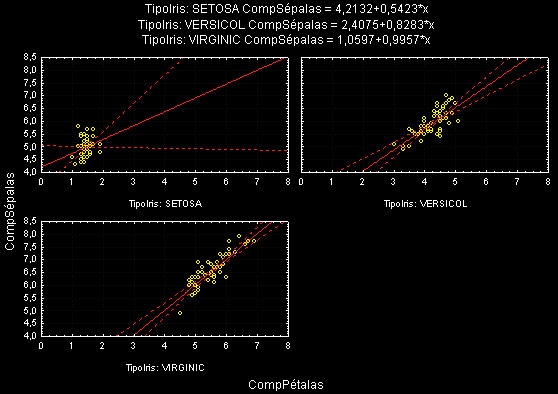
- Interpretação das Funções Discriminantes: As before, we get b (and standardized Beta) coefficients for each variable in each discriminant (now also called canonical) function, and they can be interpreted as usual: the larger the standardized coefficient, the greater is the contribution of the respective variable to the discrimination between groups. (Note that we could also interpret the structure coefficients; see below.) However, these coefficients do not tell us between which of the groups the respective functions discriminate. We can identify the nature of the discrimination for each discriminant (canonical) function by looking at the means for the functions across groups. We can also visualize how these two functions discriminate between groups by plotting the individual scores for the two discriminant functions.
- Significância das Funções Discriminantes: One can test the number of roots that add significantly to the discrimination between group. Only those found to be statistically significant should be used for interpretation; non-significant functions (roots) should be ignored.
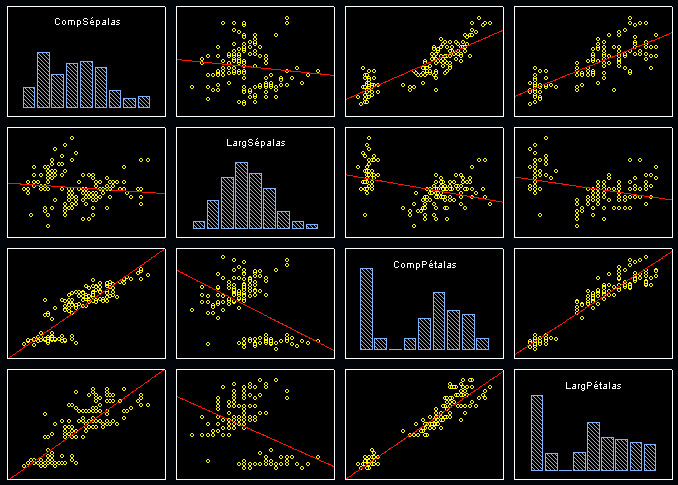
5.2.11. Segundo Exemplo Detalhado: Discriminando Diferentes Variedades de Iris


Para exemplificar a utilização de análise de discriminates vamos nos basear em um conjunto de dados bastante utilizado para demonstrar Análise de Disciminantes: o conjunto de dados sobre três espécies de flores do gênero Iris, Iris setosa (comum nos jardins da nossa ilha), Iris versicolor e Iris virginica. Estes dados foram colhidos por Fisher em 1936 e até hoje servem de exemplo de como se pode escolher funções discriminantes para um conjunto de dados composto por três classes. Os dados descrevem 150 espécimes de Iris de acordo com 4 características: comprimento das sépalas, comprimento das pétalas, largura das sépalas e largura das pétalas. A quinta váriável é a variável de grupo ou variável categórica, que associa a classificação a cada espécime ou caso observado. Apresentamos uma parte desse conjunto de dados abaixo:
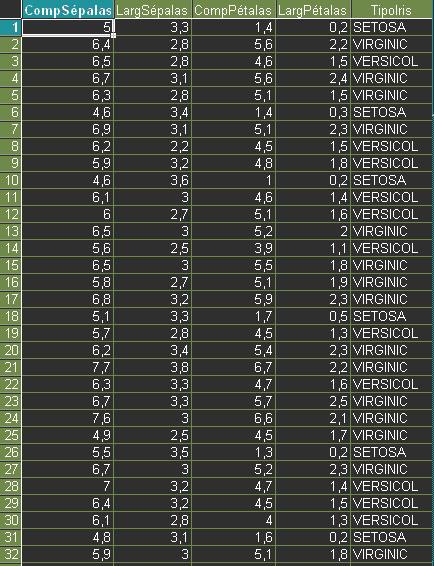
O nosso desafio
será
encontrar alguma forma de discriminar entre novos espécimes de
Iris
com base nessa informação acima.

5.2.12. Exercício de Análise de Discriminantes
Procure nos Links Úteis da página por fontes de software livre para Análise de Discriminantes. Escolha um software livre de sua preferência, baixe-o e instale-o em seu computador ou no laboratório.
A seguir, tome um conjunto de quatro sets de dados, dentre estes:
- Os dados da flor do Gênero Iris disponíveis nesta página ou em muitos repositórios de dados para teste de software estatístico.
- Os dados dos casos de câncer cerebral (gliomas) que serão fornecidos. Para você entender o câncer da glia e a classificação em graus de malignidade e o método utilizado para a geração dos dados que você vai baixar no link abaixo, veja uma explicação detalhada do trabalho aqui. Resumidamente podemos dizer que no câncer cerebral mais comum, o que ocorre nas células gliais ou de suporte do cérebro, o fator mais importante a ser determinado é a taxa de crescimento do tumor, o que vai determinar a forma de tratamento. Isto é chamado de gradação do tumor. Determinar esta taxa depende de uma série de fatores que um patologista experiente é capaz de identificar em uma lâmina de uma biópsia cerebral. Extraindo-se dados com análise de iamgesn e classificando-se estatisticamente estes dados pode-se chegra a resultados similares. Dados de 680 lâminas histopatológicas de 170 pacientes (4 por paciente) obtidas por estereotaxia coloridas com KI97 e Feulgen. Colunas da esquerda: parâmetros de análise de imagens obtidos automaticamente e teoricamente descritivos. Colunas da direita: Resultados da classificaçao manual em 1993/1995 por Dr. Harry Kolles e Prof. Feiden da Universidade de Homburg, Alemanha de acordo com a nova escala em estudo pela OMS denominada escala Saint-Anne/Mayo ou escala Daumas-Duport. Hoje padrão da OMS
- Outros dois conjuntos quaisquer que você deverá procurar também nos Links Úteis.
Tumor da Glia (glioma). Lâmina
colorida com corante
que mostra as células em divisão. 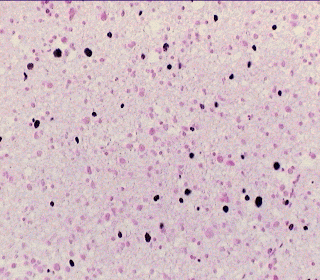 |
Árvore Expandida de Custo
Mínimo (mst)
descrevendo a relação espacial entre as células
cancerosas.  |
- Um deles buscando uma variável discriminatória para divisão em apenas dois grupos
- Outra multigrupos, buscando o conjunto de funções discriminatórias.
- No último caso utilize apenas metade dos dados para a A.D., utilizando então as funções geradas para classificar os dados restantes. Verifique a acurácia de sua classificação.
 5.3. Análise de
Agrupamentos
5.3. Análise de
Agrupamentos
O termo
Análise de Agrupamentos,
primeiramente usado por (Tyron, 1939) na realidade comporta uma
variedade
de algoritmos de classificação diferentes, todos voltados
para uma questão importante em várias áreas da
pesquisa: Como
organizar dados observados em estruturas que façam sentido, ou
como
desenvolver taxonomias capazes de classificar dados observados em
diferentes
classes. Importnate é considerar inclusive, que essas
classes
devem ser classes que ocorrem "naturalemnte" no conjunto de dados.
Biólogos, por exemplo, têm de organizar dados observados em estruturas que "façam sentido", ou seja, desenvolver taxonomias. Zoologistas confrontados com uma variedade de espécies de um determinado tipo, por exemplo, têm de conseguir classificar os espécimes observados em grupos antes que tenha sido possível descrever-se esses animais em detalhes de formas a se destacar detalhadamente as diferenças entre espécies e subespécies.
A idéia aqui é a de um processo data-driven, ou seja, dirigido pelos dados observados de forma a agrupar esses dados segundo características comuns que ocorram neles.
Este processo deve levar em conta a possibilidade de se realizar inclusive uma organização hierárquica de grupos, onde a cada nível de abstração maior, são também maiores as diferenças entre elementos contidos em cada grupo, da mesma forma que espécies animais do mesmo gênero têm muito em comum entre si, mas espécies animais que possuem apenas o filo ou a ordem em comum possuem pouca similaridade.
Os métodos de Análise de Agrupamentos estão detalhados em página especial.
 5.4.
Visão Geral de Algumas das demais Técnicas Multivariadas
de Estatística Exploratória
5.4.
Visão Geral de Algumas das demais Técnicas Multivariadas
de Estatística Exploratória
5.4.1. Análise de Correspondências (Correspondence Analysis)
A Análise de Correspondências é uma técnica descritivo-exploratória projetada para a análise de tabelas simples de duas vias e também multivias que contenham algum tipo de correspondência entre as suas linhas e colunas. Os resultados da Análise de Correspondências provêm informação similar à produzida pela Análise Fatorial (Factor Analysis), e permitem que se explore a estrutura de variáveis categóricas presentes na tabela.A tabela deste tipo mais simples e comum é a tabela de tabulação cruzada de freqüências de duas vias: Em uma análise de correspondência típica, uma tabela de tabulação cruzada é inicialmente normalizada, de forma que que as freqüências relativas ao longo de todas as células sempre somem 1,0.
Uma forma de postular a meta de uma análise típica é representar as entradas na tabela de freqüências relativas das distâncias netre colunas e linhas individuais em um espaço de dimensionalidade baixa. Isto pode ser ilustrado melhor com o exemplo abaixo.
Um exemplo: Hábitos
tabagistas X Categoria funcional na empresa (Fonte:
Greenacre (1984, p. 55))
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Suponha que você coletou os dados acerca de hábitos tabagistas mostrados na tabela acima (Greenacre 1984, p. 55):
- Você pode imaginar os os 4 valores em cada linha da tabela como pontos em um espaço tetradimensional (um vetor).
- Dessa forma é possível calcular-se a distância euclideana entre as 5 linhas da tabela neste espaço-de-linhas-da-tabela tetradimensional.
- Essas distâncias neste espaço-de-linhas resumem toda a informação sobre as similaridades entre as linhas da tabela.
- Suponha agora que você será capaz de encontrar um espaço de dimensionalidade menor onde você é capaz de colocar estes pontos de forma que as relações espaciais entre os pontos, ou seja, a informação de similaridade, sejam mantidas, pelo menos de forma geral.
- Você poderá então representar toda a informação acerca das similaridades entre linhas, que neste caso representam categorias funcionais na empresa, em um grafo 1-, 2- ou 3-dimensional.
Para uma descrição compreensiva deste método, detalhes computacionais e suas aplicações, sugere-se a leitura do texto clássico de Greenacre (1984).
5.4.2. Análise Fatorial (Factor Analysis)
A Análise Fatorial é uma técnica da ADE para: (1) reduzir o número de variáveis descrevendo um fenômeno e (2) detectar estruturas nos relacionamentos entre variáveis, classificando-as. O método é, portanto, aplicado tanto como técnica de redução de dados como de detecção de estrutura. O nome Análise Fatorial foi aplicado pela primeira vez por (Thurstone, 1931). Abaixo descreveremos muito brevemente os princípios fundamentais da Análise Fatorial sem, no entanto, entrar em detalhes matemáticos.Utilizemos um exemplo bem simples para mostrar a utilidade da redução de dados: Suponha que realizamos um estudo qualquer e que conduzimos este estudo acerca de dados biométricos de forma bastante mal projetada e que entrevistamos 100 pessoas, medindo, entre outras coisas, a altura dessas 100 pessoas tanto através da utilização de uma trena de pedreiro antiga (medida em polegadas) quanto de uma fita métrica de alfaiate (medida em centímetros). No conjunto total de dados adquiridos de cada entrevistado teremos, portanto, duas variáveis diferentes expressando exatamente a mesma coisa, porém uma com valores expressos em polegadas e outra com valores em centímetros. Se, em estudos futuros quisermos pesquisar, por exemplo, como alterações nutricionais afetam a altura das pessoas, não faz sentido algum utilizar essas duas variáveis. A altura de uma pessoa é uma só, não importanto em qual unidade de medida foi expressada.
O que nós precisamos é um método que nos diga que essas duas variáveis são redundantes proque se comportam exatamente da mesma maneira ou de maneira muito parecida e nos permitam substituir essas duas variáveis por outra, que represente de forma consolidada o comportamento de ambas. Isso é possível de ser feito quando há uma forte correlação entre as variáveis.
Vamos agora extrapolar deste estudo "bobinho" para algo que faça sentido do ponto de vista de pesquisa estatística: Suponha que você deseja estudar e medir a satisfação das pessoas com as vidas que levam.
Para tanto, você projetou um questionário de satisfação contendo muitos itens. Entre outras coisas, você pergunta aos entrevistados se eles estão satisfeitos com seus hobbies (item 1) e com qual intensidade eles estão se dedicando a um hobby (item 2). É muito provável que as respostas a estes dois itens estejam correlacionadas muito fortemente, pois é natural esperar que uma pessoa satisfeita com seu hobby também encontre prazer em praticá-lo e o pratique com freqüência e assiduidade. Se houver uma correlação alta entre essas duas variáveis, podemos concluir que são redundantes. Levantar dados redundantes é uma coisa comum em pesquisas pois: nem sempre é possível prever todos so correlacionamentos e alguma coisa pode passar despercebida, por mais óbvia que seja e também porque em muitos casos não fazemos a menor idéia de como um fenômeno se comporta e não temos como prever que duas variáveis que especificamos são redundantes.
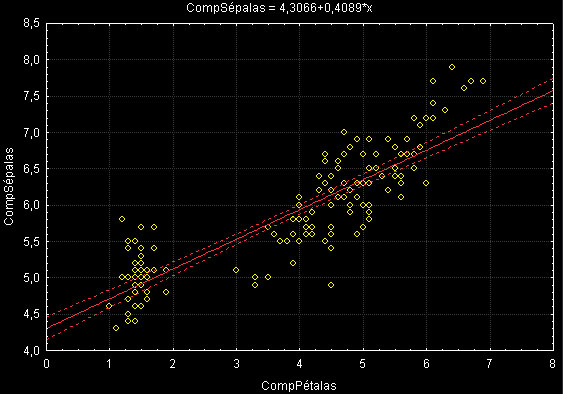
Pode-se visualizar a correlação entre duas variáveis quaisquer em um scatterplot. Neste gráfico pode-se visualizar uma linha de regressão ajustada de forma a representar o "melhor" relacionamento linear entre as duas variáveis. Se nós pudermos definir uma variável sintética capaz de aproximar a linha de regressão em um plot destes, então esta variável vais capturar a maior parte da essência dos dois aspectos do fenômeno observado descritos por essas duas variáveis. Assim reduzimos duas variáveis a´um único fator. Observe que esse fator é o resultado de uma combinação linear dessas duas variáveis. A figura abaixo mostra um scaterplot de duas variáveis com correlação positiva: altura e peso de pessoas em uma enquete. Essas duas variáveis obviamente possuem uma correlação, apesar dela não ser perfeita, e poderíamos exprimir uma combinação linear das duas através de uma variável tamanho_da_pessoa, dada pela função linear representada pela linha de regressão que interpola o scaterplot.
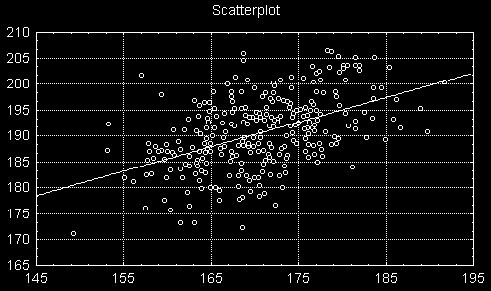
Este exemplo de combinação de duas variáveis correlacionadas em um fator é o que melhor ilustra a idéia básica da Análise Fatorial: a análise de Componentes Principais. Se extendemos o conceito para a utilização simultânea de mais de duas variáveis a computação necessária tornar-se-á mais complexa mas o princípio básico de se expressar várias variáveis através de um fator que descreve sua correlação permanece o mesmo.
A figura abaixo mostra duas variáveis sem nenhuma correlação aparente.
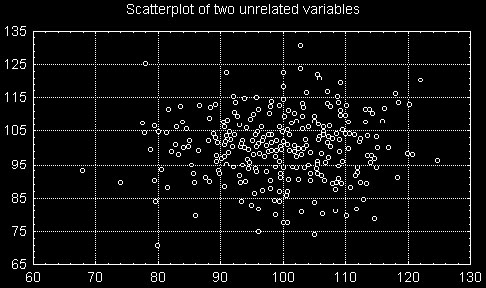
Existem muitos livros sobre Análise Fatorial, dentre eles: Stevens (1986); Cooley and Lohnes (1971); Harman (1976); Kim and Mueller, (1978a, 1978b); Lawley and Maxwell (1971); Lindeman, Merenda, and Gold (1980); Morrison (1967); or Mulaik (1972).
5.4.3. Escalonamento Multidimensional (Multidimensional Scaling)
Escalonamento Multidimensional (EMD) pode ser considerado como sendo uma outra alternativa à Análise Fatorial. De forma geral, o objetivo da análise é detectar dimensões significativas subjacentes a uma distribuição de dados que permitam ao pesquisador explicar similaridades ou dissimilaridades ou regularidades observadas entre as mensurações do fenômeno observado. Na Análise Fatorial as similaridades são expressas em uma matriz de correlação. No EMD você pode analisar qualquer tipo de matriz de similaridade ou dissimilaridade, além de matrizes de correlação.O exemplo a seguir demonstra a lógica do da Análise de Escalonamento Multidimensional. Suponha que você pegue a matriz de distâncias entre as cidades de uma determinada região. Observe que você pode considerar esta matriz de distâncias entre n cidades como uma tabela bidimensional de nXn valores escalares ou como uma lista de n pontos em um espaço n-dimensional. A seguir nós analisamos esta matriz, especificando que a meta é reproduzir estas distâncias em um espaço bidimensional. Na verdade queremos realizar uma redução dimensional dos dados, especificando que queremos passar do espaço n-dmensional, onde cada dado é representado por uma cidade com a listas das suas distâncias às outras n-1 cidades, para um espaço 2-dimensional, onde cada cidade é representada por um ponto em um espaço bidimensional (suas coordenadas cartesianas). Como resultado da análise EMD, obteremos muito provavelmente uma representação bidimensional das cidades, com as suas coordenadas.
De forma geral, EMD tenta encontrar um arranjo dos objetos dados como entrada (cidades com suas listas de distâncias a outras cidades, em nosso exemplo) em um espaço com um determinado número de dimensões (2-dimensional em nosso exemplo), de forma a reproduzir as distâncias entre os dados no espaço original. Como resultado, podemos assim explicar as relações ou distâncias entre os dados em função de algum conjunto de dimensões subjacentes.
Orientação dos Eixos na Solução Final e Significado dos Resultados
Da mesma forma que na Análise Fatorial, aqui a orientação dos eixos na solução final é arbitrária. No exemplo acima, poderíamos rotacionar o mapa de qualquer forma, que as distâncias entre as cidades permaneceriam as mesmas. Dessa forma, a orientação final dos eixos no plano cartesiano ou no espaço é decisão final do usuário do método e pode ser escolhida de forma a facilitar a compreensão intuitiva dos dados. No exemplo, poderíamos escolher os eixos norte-sul e leste-oeste.O EMD é muito mais uma maneira de "rearranjar" objetos de uma forma eficiente do que um procedimento exato. Desta forma pode-se chegar a uma configuração que descreva da melhor forma possível as similaridades entre objetos ou fenômenos. O algoritmo apenas move objetos em um espaço definido pela dimensionalidade-resultado definida pelo usuário e checa o quâ bem as distâncias originais entre objetos podem ser reproduzidas no novo espaço de representação. Para isso o algoritmo utiliza utiliza um método de minimização de uma função que iterativamente avalia diferentes configurações com o objetivo de maximizar a qualidade do ajuste (ou de minimizar o "desajuste").
O aspecto mais interessante do EMD é que ele permite que se analise qualquer tipo de distância ou matriz de similaridade. Estas similaridades podem inclusive representas valores subjetivos tomados diretamente em uma enquete como a avaliação de pessoas questionadas sobre a similaridade de produtos ou serviços oferecidos por várias empresas ou então os percentuais de concordância entre juízes o julgamento de diferentes tipos de casos, o número de vezes que um probando deixa de responder a um estímulo, etc.
Métodos de EMD já foram muito populares entre pesquisadores na área da Psicologia para registrar a percepção pessoal de probandos de determinados conjuntos de características com o objetivo de analisar as similaridades entre descritores de atributos com o objetivo de determinar a dimensionalidade de determinados tipos de percepção (veja Rosenberg, 1977). EMD também é muito popular na área de Marketing para a determinação da forma de percepção ou diferenciação de marcas de uma categoria de produtos (veja Green & Carmone, 1970).
5.4.4. Análise de Séries Temporais (Time Series Analysis)
Uma série temporal é composta por uma seqüência de medições de uma variável (ou conjunto pequeno de variáveis) que segue uma ordem não-randômica. Ao contrário das análises de seqüências de dados aleatórios estudadas na grande maioria das outras áreas da Estatística, a Análise de Séries Temporais parte do pressuposto de que o processo gerador dos dados mensurados é um processo determinístico, sendo normalmente repetitivo. Outra idéia subjacente é a de que os intervalos de tempo entre mensurações do fenômeno são constantes.A Análise de Séries Temporais tem dois objetivos:
- Identificar a natureza de um fenômeno descxrito por uma série de observações;
- Prevêr valores futuros da variável da série temporal.
Como na maioria das outras análises, supõe-se que os dados consistem de um padrão sistemático, constituído por um conjunto de componentes identificáveis, associado a ruído aleat´rorio (erro), o qual geralmente dificulta a indentificação do padrão subjacente. As técnicas de análise de séries temporais incluem uma série de filtros para a remoção de ruídos de forma a tornar a natureza doi fenômeno mais saliente.
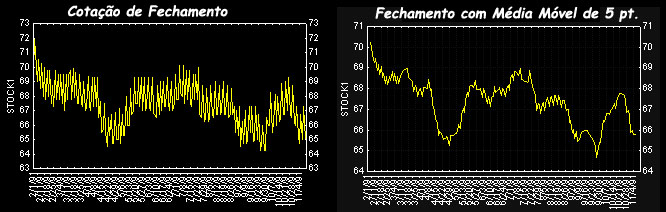
Exemplo de
série
temporal crua e da mesma série após
aplicação
de uma filtragem simples com um filtro de média móvel
sobre
5 amostragens (moving average) que suaviza o contorno do gráfico
de facilita a compreensão mais macroscópica do
fenômeno.
Tendência X Sazonalidade
A maioria das séries temporais podem ser descritas em termos de duas classes básicas de componentes: tendência e sazonalidade.- Tendência representa um componente geral sistemático, linear ou não-linear, que sofre alteração durante o tempo mas que não se repete durante o fenôeno ou pelo menos não se repete no espaço de tempo durante o qual o fenômeno foi observado ou capturado. Por exemplo: um platô sem alteração macroscópica seguido de um período de crescimento exponencial ou polinomial.
- Sazonalidade diz respeito a alterações que ocorrem ou são observadas no fenômeno a intervalos sistemáticos de tempo. Essas alterações podem apresentar as mesmas características de uma alteração tendencial, como por exemplo um platô seguido de um crescimento e seu posterior declinio, e isso repetido ao longo da série.
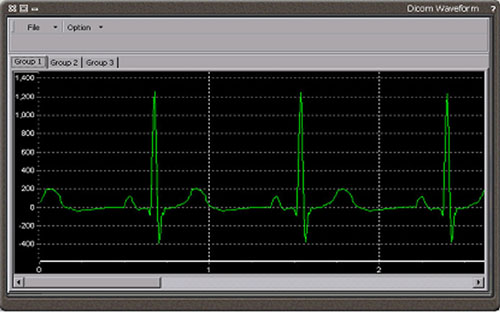
Exemplo de sazonalidade em uma série temporal produzida por um fenômeno biológico: Plot do eletrodo número 1 de um eletrocardiograma normal. Existem padrões que se repetem e chama atenção o padrão composto por um platô longo, uma alteração pequena seguido de uma alteração aguda de alta amplitude e seguido de um alteração bem longa e suave, conhecido em Cardiologia como Complexo QRS.
Este padrão geral unindo tendência e sazonalidade é muito bem ilustrado em um exemplo clássico apresentado por (Box and Jenkins, 1976, p. 531) representando os números mensais de passageiros internacionais de linhas aéreas em 12 manos consecutivos, de 1949 a 1960. Se você plotar as observações sucessivas, uma tendência global clara emerge dos dados: as linhas aéreas gozaram de um crescimento constante do numero de passageiros durante este período. O crescimento chegou a 400% em 1960 quando comparado a 1949. Ao mesmo tempo vemos um padrão local estabelecer-se na seqüência de dados: existe uma variação mensal do fluxo de passageiros que é praticamente idêntica todos os anos, mostrando que muito mais pessoas viajam nas férias do que em outros períodos do ano.
Estes dados também ilustram um tipo de padrão muito comum em séries temporais: a amplitude das modificações sazonais cresce juntamente com a tendência geral da série. Isto significa que a variância local da série está fortemente correlacionada com a média do mesmo segmento desta série, quando ambas são calculadas segmento a segmento na série, onde um segmento tem tamanho arbitrário mas bastante menor que o tamanho do conjunto de dados como um todo. Este padrão é chamado de sazonalidade multiplicativa e indica que a amplitude relativa, expressa em termos percentuais em relação ao seu segmento de dados, das alterações sazonais é constante no tempo e portanto, relacionada à tendência.
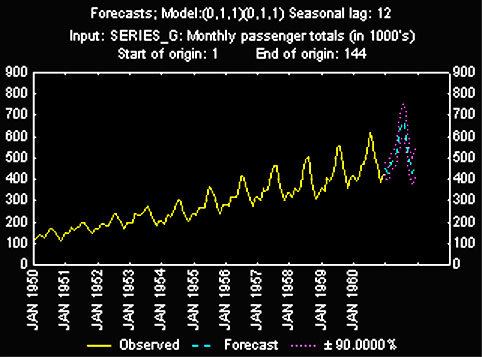
Exemplo de tendência e sazonalidade ocorrendo em conjunto.
Não existem métodos automáticos comprovados para a detecção de componentes de tendência em dados de séries temporais. No entanto, desde que a tendência seja monotônica, crescendo ou decrescendo de forma constante, esta parte da análise dos dados não é muito difícil.
Se, por outro lado, se supõe que a série temporal apresenta um ruído ou erro considerável, a primeira coisa a se fazer ao se iniciar uma análise é a suavização.
Suavização de Séries Temporais
A suavização de séries temporais através de técnicas estatísticas sempre envolve alguma forma de geração de médias locais dos dados de amostragem de forma que componentes randômicos, não sistemáticos, se cancelem mutuamente.A forma mais ismples e usual de suavização é a utilização de médias móveis (moving averages) que substitui uma amostra pela média simples ou média ponderada de um conjunto ímpar de n amostras circundantes do ponto em questão, onde n é o tamanha da janela de suavização (veja Box & Jenkins, 1976; Velleman & Hoaglin, 1981). Pode-se também ustilizar medianas, moda ou outras técnicas simples ao invés de médias. A grande vantagem de se utilizar a mediana é que o resultado é influenciado de forma menor por elementos estranhos poruzidos por ruído no processo de amostragem, produzindo curvas mais confiáveis. A grande desvantagem da mediana é que não permite que se faça suavizações ponderadas de uma forma consistente.
Na verdade, estas técnicas são exemplos restritos da técnica mais genérica chamada convolução, que pode ser aplicada tanto a dados 1D como a dados nD e que veremos mais adiante no capítulo de processamento de imagens desta disciplina. Existem muitos outros filtros de convolução, como laplacianos e filtros de gradiente que se aplica ao processamento de imagens mas que também podem ser utilizados aqui.
Ajuste de Funções
Muitas séries temporais monotônicas podem ser adquadamente aproximadas por alguma função linear, o que facilita a sua compreensão. Se existe um componente claramente monotônico não-linear, pode-se utilizar uma transformação de representação da função para um espaço logaritmico ou exponencial para linearizá-la. Existem várias técnicas estat´tisticas de Rgressão Linear e Regressão Não-Linear que podem ser utilizadas para se descobrir se existe uma função monotônica subjacente na série temporal. Muitas vezes necessita-se utilizar uma representação baseada em uma seqüência de segmentos de funções, chamada de estimativas parcias com porntos de quebra ( piecewise estimations with break points).Sazonalidade ou Repetição de Padrões
A dependência sazonal ou sazonalidade é um componente importante do padrão de uma série temporal. Ilustramos o conceito no exemplo dado anteriormente sore comportamento do número de passageiros de linhas aéreas e no exemplo de eletrocardiografia.
Sazonalidade é formalmente definida como uma dependência correlacional de ordem k entre cada i-ésimo elemento da série e o k-i-ésimo elemento (Kendall, 1976) e mensurada pela autocorrelação (correlação entre amostras diferentes da mesma variável) dos dois termos. k é usualmente denominado de retardo (lag).
A correlação de ordem k significa que a função implícita na série temporal possui correlação elevada entre segmentos seus espaçados por k amostras.
Se o erro de mensuração o o ruído não forem excessivamente grandes, a sazonalidade pode ser observada visualmente como um padrão que se repete a cada k amostras.
Autocorrelation correlogram. Seasonal patterns of time series can be examined via correlograms. The correlogram (autocorrelogram) displays graphically and numerically the autocorrelation function (ACF), that is, serial correlation coefficients (and their standard errors) for consecutive lags in a specified range of lags (e.g., 1 through 30). Ranges of two standard errors for each lag are usually marked in correlograms but typically the size of autocorrelation is of more interest than its reliability (see Elementary concepts) because we are usually interested only in very strong (and thus highly significant) autocorrelations.
Examining correlograms. While examining correlograms you should keep in mind that autocorrelations for consecutive lags are formally dependent. Consider the following example. If the first element is closely related to the second, and the second to the third, then the first element must also be somewhat related to the third one, etc. This implies that the pattern of serial dependencies can change considerably after removing the first order autocorrelation (i.e., after differencing the series with a lag of 1).
Partial autocorrelations. Another useful method to examine serial dependencies is to examine the partial autocorrelation function (PACF) - an extension of autocorrelation, where the dependence on the intermediate elements (those within the lag) is removed. In other words, the partial autocorrelation is similar to autocorrelation, except that when calculating it, the (auto) correlations with all the elements within the lag are partialled out (Box & Jenkins, 1976; see also McDowall, McCleary, Meidinger, & Hay, 1980). If a lag of 1 is specified (i.e., there are no intermediate elements within the lag), then the partial autocorrelation is equivalent to autocorrelation. In a sense, the partial autocorrelation provides a "cleaner" picture of serial dependencies for individual lags (not confounded by other serial dependencies).
Removing serial dependency. Serial dependency for a particular lag of k can be removed by differencing the series, that is converting each i'th element of the series into its difference from the (i-k)''th element. There are two major reasons for such transformations.
First, you can identify the hidden nature of seasonal dependencies in the series. Remember that, as mentioned in the previous paragraph, autocorrelations for consecutive lags are interdependent. Therefore, removing some of the autocorrelations will change other autocorrelations, that is, it may eliminate them or it may make some other seasonalities more apparent.
The other reason
for removing
seasonal dependencies is to make the series stationary, which is
necessary
for ARIMA and other techniques.
ARIMA
The modeling and forecasting procedures discussed in the Identifying Patterns in Time Series Data topic, involved knowledge about the mathematical model of the process. However, in real-life research and practice, patterns of the data are unclear, individual observations involve considerable error, and we still need not only to uncover the hidden patterns in the data but also generate forecasts. The ARIMA methodology developed by Box and Jenkins (1976) allows us to do just that; it has gained enormous popularity in many areas and research practice confirms its power and flexibility (Hoff, 1983; Pankratz, 1983; Vandaele, 1983). However, because of its power and flexibility, ARIMA is a complex technique; it is not easy to use, it requires a great deal of experience, and although it often produces satisfactory results, those results depend on the researcher's level of expertise (Bails & Peppers, 1982). The following sections will introduce the basic ideas of this methodology. For those interested in a brief, applications-oriented (non-mathematical), introduction to ARIMA methods, we recommend McDowall, McCleary, Meidinger, and Hay (1980).Autoregressive process
Most time series consist of elements that are serially dependent in the sense that one can estimate a coefficient or a set of coefficients that describe consecutive elements of the series from specific, time-lagged (previous) elements. This can be summarized in the equation:xt = x + f1*x(t-1) + f2*x(t-2) + f3*x(t-3) + ... + e
where:
x is a constant (intercept), and
f1,
f2, f3 are the autoregressive
model parameters.
Put in words,
each observation
is made up of a random error component (random shock, e)
and a linear combination of prior observations.
Stationarity requirement
Note that an autoregressive process will only be stable if the parameters are within a certain range; for example, if there is only one autoregressive parameter then it must fall within the interval of -1<f1<+1. Otherwise, past effects would accumulate and the values of successive xt' s would move towards infinity, that is, the series would not be stationary.In Time Series analysis, a stationary series has a constant mean, variance, and auto-correlation through time (i.e., seasonal dependencies have been removed via Differencing).
If there is more than one autoregressive parameter, similar (general) restrictions on the parameter values can be defined (e.g., see Box & Jenkins, 1976; Montgomery, 1990). The Time Series module automatically checks whether the stationarity requirement is met.
Moving average process. Independent from the autoregressive process, each element in the series can also be affected by the past error (or random shock) that cannot be accounted for by the autoregressive component, that is:
xt = m + et - q1*e(t-1) - q2*e(t-2) - q3*e(t-3) - ...
where
m is a constant, and
q1, q2, q3
are the moving average model parameters.
Put in words, each observation is made up of a random error component (random shock, e) and a linear combination of prior random shocks.
Invertibility requirement
Without going into too much detail, there is a "duality" between the moving average process and the autoregressive process (e.g., see Box & Jenkins, 1976; Montgomery, Johnson, & Gardiner, 1990), that is, the moving average equation above can be rewritten (inverted) into an autoregressive form (of infinite order). However, analogous to the stationarity condition described above, this can only be done if the moving average parameters follow certain conditions, that is, if the model is invertible. Otherwise, the series will not be stationary. Again, the Time Series module automatically checks whether the invertibility requirement is metDetailed discussions of the methods described in this section can be found in Anderson (1976), Box and Jenkins (1976), Kendall (1984), Kendall and Ord (1990), Montgomery, Johnson, and Gardiner (1990), Pankratz (1983), Shumway (1988), Vandaele (1983), Walker (1991), and Wei (1989).
 5.5. Glossário
de Termos Estatísticos
5.5. Glossário
de Termos Estatísticos
Esta
seção explica
alguns dos termos estatísticos mais importantes e que têm
um papel importante nos métodos que estaremos ensinando aqui. O
objetivo é rever esta matéria e refrescar a sua
memória.
Ela está detalhada em página
especial.
 5.6. Links Úteis
(Software e Dados)
5.6. Links Úteis
(Software e Dados)
- On-Line Software for Clustering and Multivariate Analysis of the Classification Society of North America (CSNA)
- On-line Software for Clustering
- Fionn Murtagh's Multivariate Data Analysis Software and Resources Page
StatLib - Data, Software and News from the Statistics Community - StatLib is a system for distributing statistical software, datasets, and information by electronic mail, FTP and WWW.