BackpropBatch and
TimeDelayBackprop
-
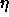 : learning parameter, specifies the step width of the
gradient descent.
: learning parameter, specifies the step width of the
gradient descent.
Typical values of
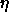 are
are 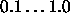 . Some small examples
actually train even faster with values above 1, like 2.0.
. Some small examples
actually train even faster with values above 1, like 2.0.
-
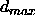 : the maximum difference
: the maximum difference
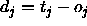 between a teaching value
between a teaching value 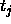 and
an output
and
an output 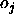 of an output unit which is tolerated,
i.e. which is propagated back as
of an output unit which is tolerated,
i.e. which is propagated back as 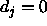 .
If values above 0.9 should be regarded as 1 and values
below 0.1 as 0, then
.
If values above 0.9 should be regarded as 1 and values
below 0.1 as 0, then 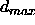 should be set to
should be set to 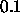 .
This prevents overtraining of the network.
.
This prevents overtraining of the network.
Typical values of
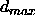 are 0, 0.1 or 0.2.
are 0, 0.1 or 0.2.
-
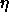 : learning parameter, specifies the step width of the
gradient descent.
: learning parameter, specifies the step width of the
gradient descent.
Typical values of
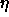 are
are 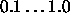 . Some small examples
actually train even faster with values above 1, like 2.0.
. Some small examples
actually train even faster with values above 1, like 2.0.
-
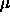 : momentum term, specifies the amount of the old weight
change (relative to 1) which is added to the current change.
: momentum term, specifies the amount of the old weight
change (relative to 1) which is added to the current change.
Typical values of
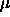 are
are 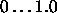 .
.
- c: flat spot elimination value, a constant value
which is added to the derivative of the activation function
to enable the network to pass flat spots of the error surface.
Typical values of c are
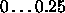 , most often
0.1 is used.
, most often
0.1 is used.
-
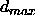 : the maximum difference
: the maximum difference
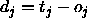 between a teaching value
between a teaching value 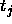 and
an output
and
an output 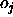 of an output unit which is tolerated,
i.e. which is propagated back as
of an output unit which is tolerated,
i.e. which is propagated back as 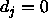 . See above.
. See above.
The general formula for Backpropagation used here is
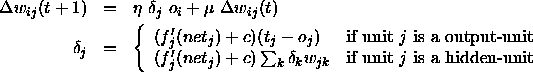
-
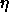 : learning parameter, specifies the step width of the
gradient descent.
: learning parameter, specifies the step width of the
gradient descent.
Typical values of
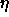 are
are 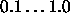 . Some small examples
actually train even faster with values above 1, like 2.0.
. Some small examples
actually train even faster with values above 1, like 2.0.
- d: weight decay term, specifies how much of the old weight
value is subtracted after learning. Try values between 0.005
and 0.3.
-
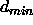 : the minimum weight that is tolerated for a
link. All links with a smaller weight will be pruned.
: the minimum weight that is tolerated for a
link. All links with a smaller weight will be pruned.
-
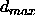 : the maximum difference
: the maximum difference
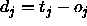 between a teaching value
between a teaching value 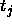 and
an output
and
an output 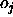 of an output unit which is tolerated,
i.e. which is propagated back as
of an output unit which is tolerated,
i.e. which is propagated back as 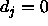 . See above.
. See above.
BatchBackpropThroughTime (BBPTT):
-
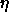 : learning parameter, specifies the step width of the
gradient descent.
: learning parameter, specifies the step width of the
gradient descent.
Typical values of
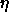 for BPTT and BBPTT are
for BPTT and BBPTT are 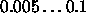 .
.
-
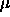 : momentum term, specifies the amount of the old weight
change (relative to 1) which is added to the current change.
: momentum term, specifies the amount of the old weight
change (relative to 1) which is added to the current change.
Typical values of
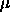 are
are 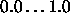 .
.
- backstep: the number of backprop steps back in time. BPTT stores a sequence of all unit activations while input patterns are applied. The activations are stored in a first-in-first-out queue for each unit. The largest backstep value supported is 10.
-
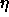 : learning parameter, specifies the step width of the
gradient descent.
: learning parameter, specifies the step width of the
gradient descent.
Typical values of
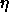 for Quickprop are
for Quickprop are 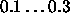 .
.
-
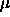 : maximum growth parameter, specifies the maximum amount
of weight change (relative to 1) which is added to the current change
: maximum growth parameter, specifies the maximum amount
of weight change (relative to 1) which is added to the current change
Typical values of
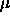 are
are 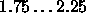 .
.
-
 : weight decay term to shrink the weights.
: weight decay term to shrink the weights.
Typical values of
 are
are 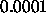 . Quickprop is rather
sensitive to this parameter. It should not be set too large.
. Quickprop is rather
sensitive to this parameter. It should not be set too large.
-
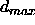 : the maximum difference
: the maximum difference
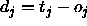 between a teaching value
between a teaching value 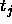 and
an output
and
an output 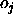 of an output unit which is tolerated,
i.e. which is propagated back as
of an output unit which is tolerated,
i.e. which is propagated back as 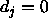 . See above.
. See above.
-
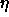 : learning parameter, specifies the step width of the
gradient descent.
: learning parameter, specifies the step width of the
gradient descent.
Typical values of
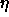 for QPTT are
for QPTT are 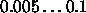 .
.
-
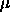 : maximum growth parameter, specifies the maximum amount
of weight change (relative to 1) which is added to the current change
: maximum growth parameter, specifies the maximum amount
of weight change (relative to 1) which is added to the current change
Typical values of
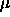 are
are 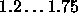 .
.
-
 : weight decay term to shrink the weights.
: weight decay term to shrink the weights.
Typical values of
 are
are 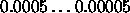 .
.
- backstep: the number of quickprop steps back in time.
QPTT stores a sequence of all unit activations while input
patterns are applied. The activations are stored in a
first-in-first-out queue for each unit.
The largest backstep value supported is 10.
-
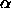 : learning parameter of the Kohonen layer.
: learning parameter of the Kohonen layer.
Typical values of
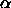 for Counterpropagation are
for Counterpropagation are 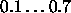 .
.
-
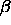 : learning parameter of the Grossberg layer.
: learning parameter of the Grossberg layer.
Typical values of
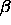 are
are 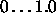 .
.
-
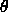 : threshold of a unit.
: threshold of a unit.
We often use a value
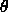 of 0.
of 0.
-
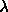 : global error magnification. This is the factor in
the formula
: global error magnification. This is the factor in
the formula 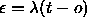 , where
, where  is
the internal activation error of a unit, t is the teaching
input and o the output of a unit.
is
the internal activation error of a unit, t is the teaching
input and o the output of a unit.
Typical values of
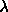 are 1. Bigger values (up to 10)
may also be used here.
are 1. Bigger values (up to 10)
may also be used here.
-
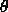 : If the error value
: If the error value 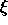 drops below this threshold
value, the adaption according to the Backpercolation algorithm
begins.
drops below this threshold
value, the adaption according to the Backpercolation algorithm
begins. 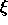 is defined as:
is defined as:
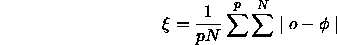
-
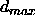 : the maximum difference
: the maximum difference
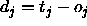 between a teaching value
between a teaching value 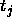 and
an output
and
an output 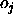 of an output unit which is tolerated,
i.e. which is propagated back as
of an output unit which is tolerated,
i.e. which is propagated back as 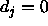 . See above.
. See above.
-
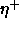 : learning rate, specifies the step width of the mean
vector
: learning rate, specifies the step width of the mean
vector 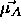 , which is nearest to a pattern
, which is nearest to a pattern 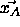 ,
towards this pattern. Remember that
,
towards this pattern. Remember that 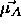 is moved only, if
is moved only, if
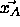 is not assigned to the correct class
is not assigned to the correct class 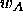 . A typical
value is 0.03.
. A typical
value is 0.03.
-
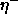 : learning rate, specifies the step width of a mean
vector
: learning rate, specifies the step width of a mean
vector 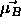 , to which a pattern of class
, to which a pattern of class 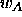 is falsely
assigned to, away from this pattern. A typical value is 0.03. Best
results can be achieved, if the condition
is falsely
assigned to, away from this pattern. A typical value is 0.03. Best
results can be achieved, if the condition 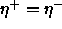 is
satisfied.
is
satisfied.
- Number of cycles you want to train the net before additive mean vectors are calculated.
- centers: determines the learning rate
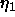 used for the
modification of center vectors.
used for the
modification of center vectors.
- bias (p): determines the learning rate
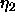 , used for
the modification of the parameters p of the base function. p
is stored as bias of the hidden units.
, used for
the modification of the parameters p of the base function. p
is stored as bias of the hidden units.
- weights: influences the training of all link weights that
are leading to the output layer as well as the training of the
bias of all output neurons.
- delta max.: If the actual error is smaller than the
maximum allowed error ( delta max.) the corresponding
weights are not changed.
- momentum:influences the amount of the momentum--term during
training.
-
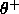 : positive threshold. To commit a new prototype,
none of the existing RBFs of the correct class may have an
activation above
: positive threshold. To commit a new prototype,
none of the existing RBFs of the correct class may have an
activation above 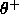
-
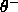 :negative threshold. During shrinking no RBF unit of
a conflicting class is allowed to have an activation above
:negative threshold. During shrinking no RBF unit of
a conflicting class is allowed to have an activation above
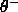 .
.
- n: the maximum number of RBF units to be diplayed in one row.
This item allows the user to control the appearance of the network
on the screen and has no influence on the performance.
-
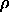 : vigilance parameter. If the quotient of active F
: vigilance parameter. If the quotient of active F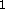 units
divided by the number of active F
units
divided by the number of active F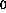 units is below
units is below 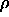 , an
ART reset is performed.
, an
ART reset is performed.
-
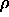 : vigilance parameter. Specifies the minimal length of the
error vector r (units
: vigilance parameter. Specifies the minimal length of the
error vector r (units 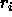 ).
).
- a: Strength of the influence of the lower level in F
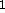 by
the middle level.
by
the middle level.
- b: Strength of the influence of the middle level in F
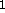 by
the upper level.
by
the upper level.
- c: Part of the length of vector p
(units
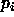 ) used to compute the error.
) used to compute the error.
-
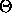 : Threshold for output function f of units
: Threshold for output function f of units 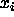 and
and
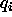 .
.
-
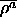 : vigilance parameter for
: vigilance parameter for 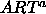 subnet.
(quotient
subnet.
(quotient 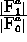 )
)
-
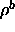 : vigilance parameter for
: vigilance parameter for 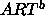 subnet.
(quotient
subnet.
(quotient 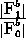 )
)
-
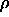 : vigilance parameter for inter ART reset control.
(quotient
: vigilance parameter for inter ART reset control.
(quotient 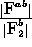 )
)
- delta
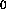 : starting values for all
: starting values for all 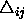 .
Default value is 0.1.
.
Default value is 0.1.
-
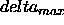 : the upper limit for the update values
: the upper limit for the update values
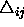 .The default value of
.The default value of 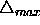 is
is 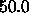 .
.
-
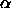 : the weight-decay determines the relationship
between the output error and to reduction in the size of the
weights. Important: Please note that the weight decay
parameter
: the weight-decay determines the relationship
between the output error and to reduction in the size of the
weights. Important: Please note that the weight decay
parameter 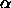 denotes the exponent, to allow comfortable
input of very small weight-decay. A choice of the third
learning parameter
denotes the exponent, to allow comfortable
input of very small weight-decay. A choice of the third
learning parameter 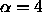 corresponds to a ratio of
weight decay term to output error of
corresponds to a ratio of
weight decay term to output error of 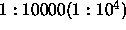 .
.
Recurrent Cascade Correlation (RCC)
CC and RCC are not learning functions themselves. They are meta algorithms to build and train optimal networks. However, they have a set of standard learning functions embedded. Here these functions require modified parameters. The embedded learning functions are:
- Backpropagation (in CC or RCC):
-
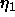 : learning parameter, specifies the step width of gradient
decent minimizing the net error.
: learning parameter, specifies the step width of gradient
decent minimizing the net error.
-
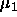 : momentum term, specifies the amount of the old weight
change, which is added to the current change.
: momentum term, specifies the amount of the old weight
change, which is added to the current change.
- c: flat spot elimination value, a constant value which is added to the derivative of the activation function to enable the network to pass flat spots on the error surface.
-
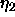 : learning parameter, specifies the step width of gradient
ascent maximizing the covariance.
: learning parameter, specifies the step width of gradient
ascent maximizing the covariance.
-
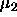 : momentum term specifies the amount of the old weight change,
which is added to the current change.
: momentum term specifies the amount of the old weight change,
which is added to the current change.
The general formula for this learning function is:
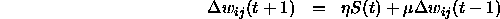
The slopes
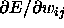 and
and 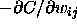 are abbreviated by S. This abbreviation is valid for all embedded functions.
By changing the sign of the gradient value
are abbreviated by S. This abbreviation is valid for all embedded functions.
By changing the sign of the gradient value 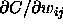 ,
the same learning function can be used to maximize the covariance and to
minimize the error.
,
the same learning function can be used to maximize the covariance and to
minimize the error.
-
- Rprop (in CC or RCC):
-
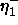 : decreasing factor, specifies the factor by which
the update-value
: decreasing factor, specifies the factor by which
the update-value 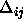 is to be decreased when minimizing the
net error. A typical value is
is to be decreased when minimizing the
net error. A typical value is 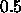 .
.
-
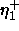 : increasing factor, specifies the factor by which
the update-value
: increasing factor, specifies the factor by which
the update-value 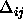 is to be increased when minimizing the
net error. A typical value is
is to be increased when minimizing the
net error. A typical value is 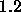
- not used.
-
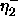 : decreasing factor, specifies the factor by which
the update-value
: decreasing factor, specifies the factor by which
the update-value 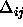 is to be decreased when maximizing the
covariance. A typical value is
is to be decreased when maximizing the
covariance. A typical value is 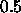 .
.
-
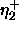 : increasing factor, specifies the factor by which
the update-value
: increasing factor, specifies the factor by which
the update-value 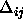 is to be increased when maximizing the
covariance. A typical value is
is to be increased when maximizing the
covariance. A typical value is 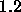
The weight change is computed by:
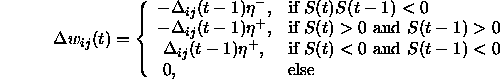
where
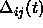 is defined as follows:
is defined as follows: 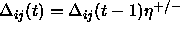 . Furthermore, the condition
. Furthermore, the condition 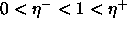 should not be violated.
should not be violated.
-
- Quickprop (in CC or RCC):
-
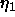 : learning parameter, specifies the step width of the
gradient descent when minimizing the net error.
A typical value is
: learning parameter, specifies the step width of the
gradient descent when minimizing the net error.
A typical value is 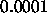
-
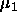 : maximum growth parameter, realizes a kind of dynamic
momentum term. A typical value is 2.0.
: maximum growth parameter, realizes a kind of dynamic
momentum term. A typical value is 2.0.
-
 : weight decay term to shrink the weights. A typical value is
: weight decay term to shrink the weights. A typical value is
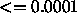 .
.
-
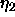 : learning parameter, specifies the step width of the
gradient ascent when maximizing the covariance.
A typical value is
: learning parameter, specifies the step width of the
gradient ascent when maximizing the covariance.
A typical value is 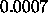
-
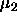 : maximum growth parameter, realizes a kind of dynamic
momentum term. A typical value is 2.0.
: maximum growth parameter, realizes a kind of dynamic
momentum term. A typical value is 2.0.
The formula used is:
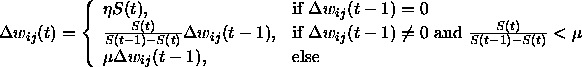
-
- h(0): Adaptation height. The initial adaptation height
can vary between 0 and 1. It determines the overall adaptation
strength.
- r(0): Adaptation radius. The initial adaptation radius
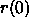 is the radius of the neighborhood of the winning unit. All
units within this radius are adapted. Values should range between 1
and the size of the map.
is the radius of the neighborhood of the winning unit. All
units within this radius are adapted. Values should range between 1
and the size of the map.
- mult_H: Decrease factor. The adaptation height decreases
monotonically after the presentation of every learning pattern. This
decrease is controlled by the decrease factor mult_H:
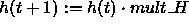
- mult_R: Decrease factor. The adaptation radius also
decreases monotonically after the presentation of every learning
pattern. This second decrease is controlled by the decrease factor
mult_R:
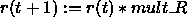
- h: Horizontal size. Since the internal representation of a network doesn't allow to determine the 2-dimensional layout of the grid, the horizontal size in units must be provided for the learning function. It is the same value as used for the creation of the network.
- n: learning parameter, specifies the step width of the
gradient descent. In [RM86] Rumelhart and McClelland
use 0.01, although values less than 0.03 are generally
acceptable.
- Ncycles: number of update cycles, specifies how many
times a pattern is propagated through the network before the
learning rule is applied. This parameter must be large enough so
that the network is relatively stable after the set number of
propagations. A value of 50 is recommended as a baseline.
Increasing the value of this parameter increases the accuracy of
the network but at a cost of processing time. Larger networks
will probably require a higher setting of Ncycles.
- n: learning parameter, specifies the step width of the
gradient descent. Values less than (1 / number of nodes) are
recommended.
- Wmax: maximum weight strength, specifies the maximum
absolute value of weight allowed in the network. A value of 1.0
is recommended, although this should be lowered if the network
experiences explosive growth in the weights and activations.
Larger networks will require lower values of Wmax.
- count: number of times the network is updated before
calculating the error.
NOTE: With this learning rule the update function RM_Synchronous has to be used which needs as update parameter the number of iterations!
- Min: lower limit of weights and biases.
Typical values are
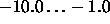 .
.
- Max: upper limit of weights and biases.
Typical values are
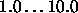 .
.
Simulated_Annealing_WTA_error and
Simulated_Annealing_WWTA_error:
- Min: lower limit of weights and biases.
Typical values are
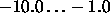 .
.
- Max: upper limit of weights and biases.
Typical values are
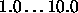 .
.
-
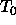 : learning parameter, specifies the Simulated Annealing
start temperature .
Typical values of
: learning parameter, specifies the Simulated Annealing
start temperature .
Typical values of 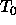 are
are 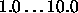 .
.
- deg: degradation term of the temperature:
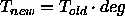 Typical values of deg are
Typical values of deg are 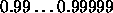 .
.
All of the following parameters are non-critical, i.e. they influence only the speed of convergence, not whether there will be success or not.
-
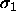 . Should satisfy
. Should satisfy 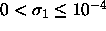 . If 0, will
be set to
. If 0, will
be set to 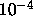 ;
;
-
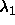 . Should satisfy
. Should satisfy 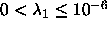 . If 0,
will be set to
. If 0,
will be set to 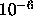 ;
;
-
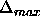 . See standard backpropagation. Can be set to 0 if
you don't know what to do with it;
. See standard backpropagation. Can be set to 0 if
you don't know what to do with it;
-
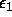 . Depends on the floating-point precision. Should be set to
. Depends on the floating-point precision. Should be set to
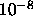 (simple precision) or to
(simple precision) or to 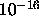 (double precision). If
0, will be set to
(double precision). If
0, will be set to 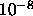 .
.