Árvore k-D

Árvore k-D

A Árvore k-D (k-Dimensional Tree) é uma Árvore Binária de Busca (BST) que permite um eficiente processamento de chaves multidimencionais. A Árvore K-D difere da Árvore Binária de Busca (BST) onde cada nível da árvore K-D se ramifica baseada numa pesquisa de chave para o nível, chamado discriminador. Definimos o discriminador no nível í como sendo í mod k para k dimensões. Por exemplo, podemos armazenar dados de coordenadas xy. Neste caso, k é 2 (há duas coordenadas), com a coordenada x definida arbitrariamente como chave 0, e a coordenada y como chave 1. Para cada nível, o discriminador alterna entre x e y. Portanto, um nodo N do nível 0 (raiz) teria em sua sub-árvore esquerda apenas nodos cujos valores de x são menores que N_x.Um nodo M ao nível 1 teria em sua sub-árvore esquerda nodos cujos valores de y são menores que M _Y.Não há restrição quanto aos valores dos pais de M_xe aos valores de x descendentes de M, desde que a decisão de ramificação feita no nodo M seja baseada somente na coordenada y.

Para um dado conjunto S = {p1,..., pn} em n pontos em l R^d, às vezes é importante podermos responder a extensão da pesquisa ortogonal em S; isto é, dada uma caixa B para consulta em l R^d, gostaríamos de rapidamente determinar o subconjunto de pontos de S que estão em B.

Foram sugeridas várias estruturas de dados para resolver este problema. Teoricamente a estrutura de dados que realiza a tarefa em tempo inferior é a árvore k-D.

árvore k-D é um dos métodos mais rápidos para resolver problemas de pesquisa de pontos vizinhos. Necessita somente uma média de O(LogN) operações para procurar uma série de dados em vez de N² operações requeridas normalmente. A árvore k-D foi proposto primeiramente por J. L. Bentley em 1975. Desde então ele tem sofrido modificações para melhorar seu desempenho. O árvore k-D é basicamanete um tipo de árvore binária que divide os pontos de dados em parcelas menores mais viáveis (buckets). Minimizando, assim, o número dos pontos de dados que necessitam ser procurados. Esta estrutura de dados é muito usada durante a pesquisa em extensão ortogonal. Imagine que você deseja encontrar um conjunto de pontos que caem em um dado retângulo no plano. Fornecendo uma árvore k-D dos pontos em questão é possível encontrar os pontos resultantes em O(sqrt(n)+k), onde n é o número de pontos e k é o número de pontos do resultado.

Construindo a Árvore:

Algoritmos típicos constroem árvore k-Ds dividindo os conjuntos de pontos. Cada nodo na árvore está definido em um plano por uma das dimensões das partições do conjunto de pontos em esquerda/direita (ou acima/abaixo), cada um com a metade dos pontos do nodo pai. Os filhos são divididos novamente ao meio, usando planos com dimensão diferente. As divisões param após LogN níveis, com cada ponto em sua própria folha.

Os planos cortados ao longo de qualquer caminho da raiz para outro nodo definem caixas com difrerentes tamanhos, e cada corte nos planos subseqüentes dividem estas caixas em duas. Cada caixa está definida em 2k planos onde k é o número de dimensões.

A árvore é construída por uma função recursiva. A função verifica se os dados que ela está olhando atualmente são pequenos o bastante para a divisão ser encerrada. Se for pequena o bastante, a função então marca estes dados como uma caixa e retorna para a chamada da função. Agora, se os dados ainda são muito grandes, necessitam ser divididos novamente. Assim a função divide perto do número médio da linha central com a distância maior entre os pontos máximo e mínimo. Então a função faz uma chamada recursiva passando as duas partes da divisão como parâmetros.

Depois de pronto, retornará a raiz da árvore criada quando foi realizada a chamada da função. A árvore é composta de dois tipos de nodos, o folhas e o internos:

Os nodos-folha são essencialmente caixas dos dados que estão em um determinado nível de busca.
Os nodos internos têm dois filhos, esquerda e direita, que podem ser folhas ou internos.

Tipos diferentes de árvore k-Ds diferem como o plano é selecionado. Opções incluem:

Circuito pelas dimensões (discriminadores) - divide primeiro em d₁, então d₂,...,d_k, antes de voltar para d₁.
Corte ao longo da dimensão maior - seleciona a dimensão de partição para fazer as caixas resultantes como quadrado ou cubo - sempre que possível. Selecionar um plano para dividir os pontos pela metade não significa selecionar uma divisão no meio da caixa, uma vez que todos os pontos podem estar no mesmo lado.
Quadtrees ou Octtrees - em vez de dividir com planos únicos, use todos os eixos paralelos que atravessam um determinado ponto de partição. Em duas dimensões, isto significa criar quatro filhos, em 3D isto significa oito filhos. Quadtrees aparecem particularmente em imagens onde as folhas sugerem que todos o pixels nas regiões têm a mesma cor.

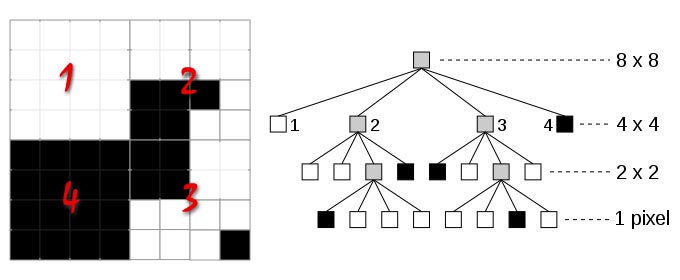
Quadtree de uma imagem: os números mostram o primeiro nível da árvore, que divide a imagem em 4 nodos, onde os nodos 1 e 4 são folhas, respectivamente de cor branca e preta. Sempre que uma área só possue pixels de um mesmo valor, não se subdivide maisi a árvore e tem-se uma foiha.

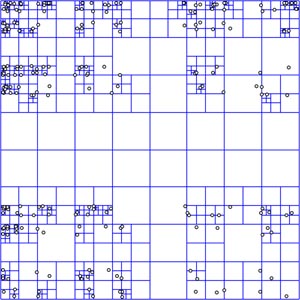Quadtree representando um conjunto de pontos. Observe que, ao conttrário da árvore k-D, onde uma aresta está sempre sobre um ponto, na quadtree a subdivisão do espaço é homogênea e um ponto pode cair "dentro" de um quadrado.

Algoritmo Árvore k-D Balanceada:

Uma árvore k-D pode ser construída usando o algoritmo que segue:

Entrada: Um conjunto de pontos P e a profundidade atual prof

Saida: A raiz de uma árvore k-D armazenando P

Algoritmo ConstroiArvKD(P,prof)

1. SE P contém apenas um ponto then

2. return uma folha contendo este ponto

3. SENÃO SE prof é plano ENTÃO

4.      divida P em dois subconjuntos com uma linha vertical pela coordenada x mediana dos pontos em P.
        P1 é o conjunto de pontos da esquerda e P2 o conjunto de pontos da direita.
        Pontos exatamente na linha pertencem a P1

5. SENÃO

6.           divida P em dois subconjuntos com uma linha horizontal pela coordenada y mediana dos pontos em P.
             P1 é o conjunto de pontos acima da linha e P2 o conjunto de pontos abaixo da linha.
             Pontos exatamente na linha pertencem a P1.

7. Vright <- ConstroiArvKD(P1,prof+1).

8. Vleft <- ConstroiArvKD(P2,prof+1).

9. Crie um nodo V com Vright e Vleft juntamente com seus filhos direito e esquerdo, respectivamente.

10. retorne V.

O autor afirma que este algoritmo pode ser executado em tempo O(n log n) e usa O(n) armazenamento.

Exibição demonstrativa interativa da construção de uma árvore k-D 2D:

A demonstração interativa requer que Java esteja ativado em seu browser. Requer Java 1.1 ou superior.
Pessoalmente eu testei em: Netscape 7.2 e em Firefox 3.5.4 e funcionou. Em IE 8 não funcionou.

A área que está sendo controlada é marcada com um retângulo no painel de pontos:

Se a área contém só um ponto então um nodo folha é criado no painel da árvore. Cada nodo folha representa um ponto e tem o número deste ponto impresso em seu interior.
Se a área contém mais de um nodo então a área é dividida usando uma linha horizontal ou vertical e são criadas, assim, duas áreas menores. Um nodo é acrescentado à árvore k-D no painel da árvore. Os nodos internos da árvore são marcados com uma linha horizontal ou vertical deixando fácil verificar se corresponde a uma linha horizontal ou vertical no conjunto de pontos. Os nodos são acrescentados pela profundidade primeiro, mas a ordem não é importante para a correta execução do algoritmo.

A linha e nodo no painel da árvore que foram há pouco adicionados são mais grossos que as outras linhas.

Os botões na interface têm as seguintes funções:

Generate Points: Gera um novo conjunto de pontos. O número de pontos usado é determinado pelo campo # of points e deve ser pelo menos 1 e não mais que 50.
Next Step: Acrescenta um novo nodo à árvore k-D. Quando a árvore estiver completa o botão ficará desativado.
Restart: Reinicia a construção da árvore k-D mas sem criar um novo conjunto de pontos

Divisão de um conjunto de pontos induzida por uma árvore k-D:

Pesquisando na Árvore:

A função de busca é também um algoritmo recursivo. A função ramifica-se através da árvore até que encontre a caixa a que o registro da consulta pertence. Então faz um array com os valores próximos usando os pontos da caixa. Avalia se é preciso verificar outras caixas (sem pontos suficientes ou procurando pontos próximos). Se não tiver que verificar outras caixas, termina a busca e retorna o resultado. Se não, ramifica-se nos pares de caixas seguintes até que tenha pontos suficientes, e os mais próximos.

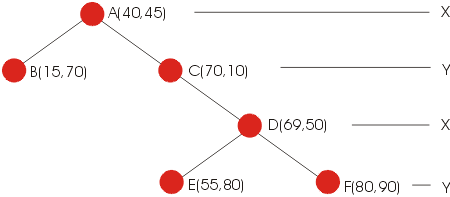
Pesquisar na árvore k-D por um registro com uma coordenada xy específica é como pesquisar em uma Arvore Binária de Pesquisa (BST), exceto que cada nível da árvore é associado com um discriminador. Por exemplo, assuma que estamos procurando no Banco de Dados por um registro localizado no ponto P=(69,50). Começamos pela comparação P com o endereço do ponto armazenado na raiz Se o endereço de P coincidir com o endereço do registro A, então a pesquisa retornará com sucesso. Se neste exemplo as posições não coincidirem (o endereço de A(40,50) édiferente de (69,50), a pesquisa deve continuar a descer de nível. O valor x do nodo A é comparado com o P para determinar em qual ramo seguir. Se o valor Ax de 40 for menor que o valor pesquisado de 69, nos direcionaremos para a subárvore da direita (todos nodos com valor de x maior ou igual a 40 estão na subárvore da direita). 0 valor de Ay não afeta a decisão de qual ramo se direcionar neste nível. Num segundo nível, P não coincide com a posição do registro C, então, outro ramo deve ser seguido. Entretanto, neste nível, o ramo a ser seguido é baseado nos valores de y de P e do registro C ( veja: 1 mod 2 = 1 ... nivel mod dimension = critério, 1 corresponde à coordenada y). Se o valor de Cy de 10 for menor que o valor Py de 5O, nós seguimos para a direita. Neste ponto, P é comparado com a posição de D. A comparação é feita e a pesquisa retorna com sucesso. Assim como na Árvore Binária de Busca (BST), se o resultado da pesquisa for um ponteiro nulo, então, o conteúdo pesquisado não está contido na árvore.

Assuma que nós desejamos imprimir a lista de todos registros que estão à uma certa distância d do ponto dado P. Nós usaremos a distância Euclidiana, que é: o ponto P é definido para estar dentro da distância d do ponto N se:

SQRT((Px-Nx)²+(Py-Ny)²)<=d

Se o resultado do processo de pesquisa for um nodo cujo valor do discriminador for maior que o d acima, então não é possível que qualquer registro na subárvore direita possa estar dentro da distância d do valor procurado, desde que todas chaves na dimensão são grandes também. Similarmente, se o valor do discriminador do nodo corrente for d menor que o valor procurado, então nenhum registro da subárvore esquerda pode estar dentro do raio. Em alguns casos, a subárvore em questão não precisa ser analisada, poupando muito tempo. Geralmente o número de nodos que devem ser analisados durante a pesquisa é relacionado ao número de registros de dados que caem na pesquisa em questão.

Por exemplo, assuma que a pesquisa será realizada para encontrar todos nodos na figura com 25 unidades do ponto (25,65). A pesquisa começa no nodo raiz, que contém o registro A(40,45), que é exatamente 25 unidades do ponto procurado, deve ser reportado. Um procedimento de pesquisa então determinará qual ramo da árvore pegar. 0 círculo de pesquisa se estende para ambos esquerda e direita da linha divisória de A, então ambos ramos da árvore devem ser pesquisados. A subárvore da esquerda é processada primeiro. Aqui, o registro B é checado e encontrado para cair no círculo de pesquisa. Se o nodo B não tem filhos, o processo da subárvore da esquerda está completo. 0 processo da subárvore direita de A começa então. As coordenadas do registro C são checadas, e ao ser encontrado não cairá no círculo de pesquisa. Assim, não deverá ser reportado. Entretanto, é possível que nodos dentro das subárvores de C possam cair dentro do círculo de pesquisa. Já que o nível de C é 1, o discriminador para este nivel é a coordenada y. Já que 6525 >10, nenhum registro da subárvore esquerda de C pode cair no círculo de pesquisa.

Portanto, a subárvore esquerda de C não precisa ser analisada. Entretanto, nodos da subárvore direita de C podem cair no círculo. Portanto é necessário proceder para o nodo contendo o registro D. Novamente, D está fora do círculo de pesquisa. Já que 25+25<69, nenhum registro na subárvore direita de D pode cair no círculo de pesquisa. Portanto apenas a subárvore esquerda de D precisa ser procurada. Então é necessário comparar as coordenadas de E contra o círculo de pesquisa. o Registro E cai fora do círculo de pesquisa, e o processamento está completo.

Quando um nodo é visitado, uma função é usada para checar a distância euclidiana entre o nodo e o ponto pesquisado. Isso não é suficiente para checar se a diferença entre as coordenadas x e y são menores que a distância pesquisada porque o registro poderia estar fora do círculo de pesquisa.

Inserindo novo nodo na Árvore:

Inserir um novo nodo na árvore kd é similar à inserção da Árvore Binária de Busca (BST). O procedimento de pesquisa na árvore kd é realizado até que um ponteiro nulo seja encontrado, indicando um local propício para inserir um novo nodo. Por exemplo, inserir um registro no endereço (10,50) na árvore kd da figura requer uma pesquisa para o nodo E. Neste ponto um novo registro é inserido na subárvore esquerda de E.

Deletando um nodo da Árvore:

Deletar um nodo da árvore kd é similar ao deletar de uma Árvore Binária de Busca (BST), mas ligeiramente mais difícil. Assim como delecar de uma Árvore Binária de Busca (BST), o primeiro passo é encontrar o nodo (chamado N) a ser deletado. É necessário encontrar o filho de N que será usado para substituir N na árvore. Se N não tiver filhos ele é substituído por um ponteiro nulo. Note que se N tem um filho que por sua vez também tem, não podemos simplesmente gravar no lugar de N o ponteiro para seu filho, como seria feito na Árvore Binária de Busca (BST). Para fazer isso então, teríamos de mudar o nível de todos nodos na subárvore, e portando o discriminador usado para a pesquisa também seria mudado. 0 resultado é que a subárvore não seria mais uma árvore kd porque violaria a propriedade da Arvore Binária de Pesquisa (BST) para o discriminador.

Similar à delação na Árvore Binária de Busca (BST), o registro armazenado em N deve ser substituído pelo registro da subárvore direita com o menor valor do discriminador de N ou pelo registro da subárvore esquerda com o maior valor para o discriminador. Assuma que N estava em um nível ímpar e portanto y é o discriminador. N poderia ser substituído pelo registro da subárvore da direita com o menor valor de y (chamado de Y_MIN). O Problema é que Y_MIN não é necessariamente o nodo mais à esquerda, assim como na Árvore Binária de Busca (BST). É necessário modificar o procedimento que encontra o menor valor de y na subárvore direita.

Uma chamada recursiva para a rotina de deleção removerá então o Y_MIN da árvore. Finalmente, o registro Y_MIN é substituto para o registro do nodo N.

Note que podemos substituir o nodo a ser deletado pelo nodo da subárvore direita com o menor valor apenas se a subárvore direita existir. Se não existir, então, o elemento da substituição deverá ser encontrado na subárvore esquerda. Infelizmente, não é satisfatório substituir o registro N com o registro que possui o maior valor do discriminador da subárvore esquerda, porque este novo valor pode ser duplicado. Então nós teríamos iguais valores para o discriminador na subárvore esquerda de N. Isso viola a regra para árvores kd. Felizmente, há uma solução simples para este problema. Primeiramente, moveremos a subárvore esquerda de N para tornarse a subárvore direita (simplesmente trocaremos os ponteiros das subárvores direita e esquerda de N). Neste momento, nós procederemos com o processo normal de deleção, substituindo o registro N a ser deletado com o registro contendo o menor valor do discriminador da subárvore que é agora a direita.

Aplicações:

< style="font-family: helvetica,arial,sans-serif;">Idealmente, nossas partições dividem ambos os espaços uniformemente (assegurando regiões agradáveis, regulares) e o conjunto de pontos uniformemente (assegurando uma árvore de altura log), mas isto pode ser impossível para um determinado conjunto de pontos. As vantagens de caixas as grandes ficam claras em muitas aplicações de árvore k-D:

<>Localização de Ponto - para identificar em qual caixa um determinado ponto q está. Nós começamos na raiz e testamos qual lado do plano da partição contém q. Repetindo este processo no nodo filho apropriado, nós caminhamos na árvore para achar a folha que contém q em tempo proporcional à sua altura.
<>Busca do Vizinho mais Próximo (nearest neighbor) - para achar o ponto em S mais próximo de um ponto q, nós executamos a localização de ponto para achar a caixa c que contém q. Desde que c seja limitado por algum ponto p, nós podemos calcular a distância d(p,q) de p para q. Para encontrar o ponto mais próximo temos que percorrer todas as caixas a uma distância d(p,q) de c. Com caixas maiores, menos precisariam ser testadas.
<>Procura de chave parcial - suponha que queremos achar um ponto p em S, mas não temos informação suficientes sobre p. Dizemos que estamos procurando alguém de idade 35 e altura 1,75'' mas de peso desconhecido em uma 3d-tree com idade, peso, e altura. A partir da raiz, nós podemos identificar o decendente correto para todos menos a dimensão de peso. Para ter certeza que achamos o ponto certo, temos que procurar em ambos os filhos deste nodo. Tal procura de chave parcial pode ser substancialmente mais rápida que conferindo todos os pontos com a chave.

árvore k-D é uma estrutura de dados muito eficiente para números pequenos e moderados de dimensões, diga de 2 até talvez 20 dimensões. Com os aumentos de dimensão, ela perde a efetividade, porque muitas caixas terão que ser procuradas dentro de um determinado raio de um ponto para a busca do vizinho mais próximo. Também, o número de vizinhos para qualquer caixa cresce 2k e eventualmente fica intratável.

Exemplo de árvore k-D e Árvore Binária de Busca:

pontos vermelhos: cidades e coordenadas

linhas pretas: Grade da árvore k-D

linhas azuis: Bordas da BST

círculos amarelos: nós visitados ao atravessar a árvore

círculo cinzento: círculo de busca

A demonstração interativa requer que Java esteja ativado em seu browser. Requer Java 1.1 ou superior.
Pessoalmente eu testei em: Netscape 7.2 e funcionou. Em IE 8 e em Firefox 3.5 não funcionou.

Bibliografia: