Áreas de Aplicação de Linguagens Funcionais

• 4.1.1. Exemplo: Árvore Expandida de Custo Mínimo
  O Algoritmo de Kruskal
• 4.1.2. Implementação do algoritmo de Kruskal em LISP:
• 4.1.3. Trabalho

[RTF] [PostScript]

4.1. Matemática Discreta:Teoria de Grafos

• A facilidade com que linguagens funcionais nos permitem expressar conjuntos, seqüências e recursão as indicam como um instrumento para a implementação de problemas da matemática discreta, como teoria de grafos, topologia, etc.
• Um bom exemplo de aplicação nos fornece a Teoria de Grafos, onde podemos muito facilmente representar:
• Nodos como um conjunto de arestas que ali se encontram,
• Arestas como um par de vertices. Este par pode ser ordenado em digrafos, ou simplesment eum conjunto de vertices sem ordem.
  Podemos tambem representar arestas em hipergrafos como uma tríade ou mais de vertices.
• Podemos representar arestas com custos associados como uma lista contendo os vertices e os custos (caso sejam diversos custos) de uma aresta.
• Muitos problemas ou são recursivos ou usam pilhas como armazenamento intermediário.
• Muitos problemas precisam de estruturas de dados que são arvores ou grafos cíclicos.
• Tudo isto pode ser representado otimamente com listas.

4.1.1. Exemplo: Árvore Expandida de Custo Mínimo
O Algoritmo de Kruskal

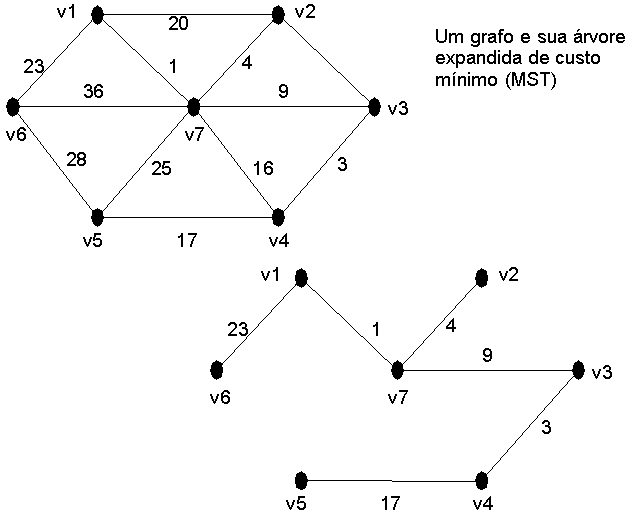
Relembrando: Dado grafo G(V, E) conexo e com uma função de custo associada a cada uma de suas arestas, uma árvore expandida de custo mínimo (MST) é uma árvore que contém todos os vértices de G e onde a soma dos custos das arestas é mínimo. Um grafo pode ter mais de uma árvore expandida de custo mínimo.

O cálculo da árvore expandida de custo mínimo é relativamente rápido e é da ordem O(n log n) para n arestas, tendendo a O(n) com número crescente de arestas.

O Algoritmo de Kruskal

Este algoritmo utiliza três conjuntos E, T e VS. T é usado para guardar as arestas da árvore expandida. O algoritmo trabalha transformando uma floresta expandida de G em uma única árvore. O conjunto VS contém os conjuntos das árvores da floresta expandida. Inicialmente VS contém todos os vértices de G, onde cada vértice é um conjunto unitário. As arestas são escolhidas po ordem crescente de custo. Quando uma aresta une duas subárvores da floresta expandida, estas são unidas em VS, quando não, ela é descartada.

Algoritmo:

Inicio 
   Faça T <- 0; VS <- 0;
   Construa uma fila de prioridade (Q) contendo todas as 
   arestas de E;
   Para cada vértice v em V faça: adicione {v} em VS;
   Enquanto |VS| > 1 faça
      Escolha {v,w}, uma aresta em Q de menor custo;
      Apague {v,w} de Q;
      Se v e w estão em conjuntos diferentes w1 e w2
      pertencentes a VS, então:
         Substitua w1 e w2 por w1 união w2;
         Adicione (v,w) a T;
      fim se
   fim enquanto
FIM

• Como implementar isto em LISP?

4.1.2. Implementação do algoritmo de Kruskal em LISP:

• Implementação de uma estrutura representando um grafo:
  
  Exemplo: Grafo da figura anterior
  

(setq Grafo '( 
  (v1 v7 1) (v4 v5 17) 
  (v3 v4 3) (v1 v2 20) 
  (v2 v7 4) (v1 v6 23) 
  (v3 v7 4) (v1 v6 23) 
  (v3 v7 9) (v5 v7 25) 
  (v2 v3 15) (v5 v6 28) 
  (v4 v7 16) (v6 v7 36) ) ) 

• Podemos expressar um grafo naturalmente atraves de uma lista com sublistas onde cada sublista é uma aresta com os seus dois vértices e o seu custo.

4.1.2.1. Implementação: [arquivo em LISP]

;---------------------------------------------------
(defun kruskal (UmGrafo)
  ; Inicializa‡oes
  (setq ConjuntoDeVertices '())
  (setq Arvore '())
  ; Ordene as arestas do grafo por custo e ponha em uma fila de prioridade
  (setq FilaDePrioridade 
        (sort UmGrafo 
              #'(lambda (aresta1 aresta2)(< (nth 2 aresta1) (nth 2 aresta2)))))
              ; Observe a utilização de uma função lambda aqui:
              ; O fato de que a função só vai ser usada aqui não justifica
              ; que criemos uma função com defun e um nome. Simplesmente usamos
              ; uma função sem nome (lambda) declarada diretamente onde é usada.
  ; Para cada vertice v adicione {v} ao conjunto de vertices.
  (dolist (umaAresta FilaDePrioridade)
    (setf ConjuntoDeVertices
          (adjoin (list (nth 0 umaAresta)) ConjuntoDeVertices :test #'equal))
    ; Adiciona um conj.unitario com o primeiro vertice de cada aresta 
    ; ao conjunto de vertices, caso ainda nao perten‡a.
    (setf ConjuntoDeVertices
          (adjoin (list (nth 1 umaAresta)) ConjuntoDeVertices :test #'equal))
    ; Faz o mesmo com o segundo vertice.
  ) ;fim para
  (loop 
    ; Repita enquanto ConjuntoDeVertices nao for um conjunto unitario.
    (when (equal (cdr ConjuntoDeVertices) nil) (return))
    ; Retire a proxima aresta (v,w) do conjunto de arestas
    (setq proximaAresta (pop FilaDePrioridade))
    ; Determine os conjuntos w1 e w2 aos quais v e w pertencem.
    (setq w1 nil) (setq w2 nil) 
    (dolist (umGrupo ConjuntoDeVertices) 
      ; Olhe se v e w sao elementos de cada um dos grupos de vertices.
      (when (member (nth 0 proximaAresta) umGrupo) (setf w1 umGrupo))
      (when (member (nth 1 proximaAresta) umGrupo) (setf w2 umGrupo))
    ) ; fim para
    (when (not (equal w1 w2))
      (progn
        ; Retire w1 e w2 do conjunto de conjuntos de vertices.
        (setf ConjuntoDeVertices
              (set-difference ConjuntoDeVertices (list w1 w2) :test #'equal))
        ; Inclua w1 uniao w2 ao conjunto.
        (push (union w1 w2) ConjuntoDeVertices)
        ; Adicione a aresta aa arvore.
        (push proximaAresta Arvore)
      )
    ) ; fim se
  ) ;fim enquanto
  Arvore
)

4.1.3. Trabalho

Implemente você um programa em LISP resolvendo algum problema de Teoria de Grafos ou de outra área da Matemática Discreta. Escolha um problema cuja complexidade estrutural justifique que seja usado como exemplo. Sugestão: O algoritmo de Dijkstra para o cálculo da árvore expandida de custo mínimo:

Algoritmo MST de Dijkstra
Entrada: O grafo G(V,E), representado pela lista de arestas e seus custos.

P1: Faça T <- 0;
P2: Construa uma fila de prioridade (Q) contendo todas 
    as arestas de E;
P3: Escolha (v,w), uma aresta em Q de menor custo;
P4: Enquanto |V| > 0 faça
       Retire (v,w) de Q;
       Adicione (v,w) a T;
       Apague v,w de V e inclua em V1;
       Escolha (v,w), a aresta em Q de menor custo, tal
       que v esteja em V e w em V1.