


In many disciplines, signals and systems problems in N-dimensions are solved either in the time or frequency domains. In the time-domain, these problems are solved using classical methods for solving differential/difference equations. In the frequency-domain, problems are solved by addressing algebraic equations. Where is the advantage? If integration and differentiation can be transformed into algebraic equations then we have facilitated the problem solving process.
In general, signals and system problems, can either be solved using differential/difference or albebraic equations. The tools that allow us to go back and forth from one domain to the other are known as transforms. Two widely used transforms are the Laplace Transform and the Fourier Transform, and both are related. Here we will look at the Discrete Fourier Transform (DFT).

The Discrete Fourier Transform (DFT) for a 1D signal of length N is defined as
![]()
![]()
where both f(x) and F(u) are periodic with the same period N.
Suppose the image, f(x,y) (2D signal), has size 128x128
f(x,y) = 1 for x <= 64 and 0 elsewhere:

|
|---|
The DFT generates a complex image, with real and imaginary parts. In practice we compute the DFT of real functions (images). Another way of looking at the DFT is to see its Magnitude and Phase spectrums. The magnitude spectrum is an even function, i.e. M(u) = M(-u). The phase spectrum is an odd function, i.e. - P(u) = P(-u ). Both spectrums are periodic with periods N and M, where N is the size of the image's width and M is the height. In general we operate on square images, thus, N = M. Also, in general the spectrums are displayed with the DC component, i.e. its (0,0) at the center.
The magnitude spectrum of our image f(x,y) is

|
|---|
The image, f(x,y), has a constant value in any vertical line. It is expected to have magnitude spectrum values different than zero only in the middle line, i.e. F(0,v) != 0.
Extracting a 1D profile of the DFT, horizontal line 64, and plotting it yields
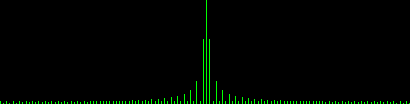
|
|---|
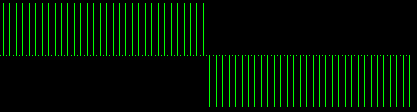
|
|---|
Is there a connection between the 1D DFT and a N-dimensional DFT? Analytically, we can compute the DFT of the 1D signal of length 128 with the equation
![]()
Printing the pixel values of the DFT we get a list of the real and imaginary numbers
...
real imaginary
61 ( 2.385244779e-17, 0.1059114784)
62 ( 0.0078125, -0)
63 ( 1.880985883e-17, 0.3182459772)
64 ( 0.5078125, 0)
65 ( 1.301042607e-17, -0.3182459772)
66 ( 0.0078125, -0)
67 ( 1.908195824e-17, -0.1059114784)
68 ( 0.0078125, -0)
...
Recall, position 64 gives F(0) = 65/128, F(1)= 0-j0.31 = conjugate of F(-1), which are properties of the Fourier transform.
... Magnitude Phase 61 0.1059114784 1.570796371 62 0.0078125 -0 63 0.3182459772 1.570796371 64 0.5078125 0 65 0.3182459772 -1.570796371 66 0.0078125 -0 67 0.1059114784 -1.570796371 68 0.0078125 -0 ...