

Generation of 1D and 2D sinusoidal waves are essential for the creation of test patterns, color maps, filter kernels, etc, used either in the spatial or frequency domains.

A discrete sinusoidal signal is defined by its length (W), amplitude (A), its period (T) or frequency (f) and phase (phi). We can measure the period in number of pixels (samples), and the frequency in number of cycles per pixel (or cycles per sample). You can also specify the period by n (number of cycles within the signal length W).
![]()
![]()
![]()
|
|---|
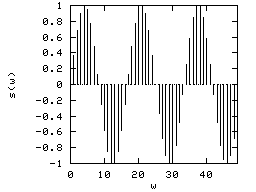
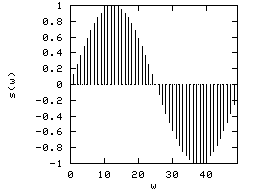
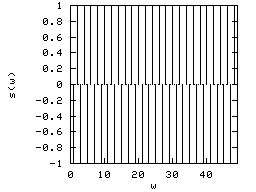
The maximum period we have to fill the entire signal is the signal length (T=W). Recall the sampling theorem; the minimum period we can sample a sinusoid wave is 2 pixels.
|
|
|---|---|
| a) | b) |

For 2D images, a sinusoid wave can also be generated. The image represents a 2D sinusoid which can run in any direction. We can specify this image by specifying frequency and phase parameters in each direction. Below is a 2D wave. Its effective period is 14.14 pixels and the wave direction is 45 degrees.
![]()
![]()
![]()
![]()

|
|---|
|
|
|---|---|
| a) | b) |
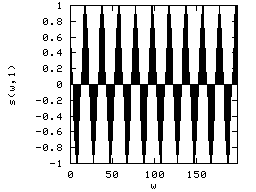
The maximum period and minimum period waves we can generate with the above image size are T=200 in the width direction and T=1.41 in 45 degrees direction. It is important to remember that the minimum period is independent of the image size.

|

|
|---|---|
| a) | b) |
Note: in the high frequency image, a small portion of it is zoomed and displayed over it.