|
 |
|
|
Data-Driven Approaches for decision Making in Automated Tumour Grading.- An Example in Astrocytoma Grading -H. Kollesa, A. v.Wangenheimb, J. Rahmelb, I. Niedermayera, W. Feidena
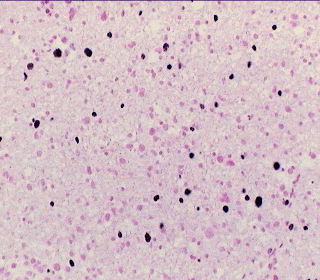
Vol. 18 No. 4 August 1996 1. SummaryIn this article four data-driven approaches for automated tumour grading purposes based on morphometric data are compared. Apart from the statistical procedure of linear discriminant analysis, three other approaches from the field of neural computing are considered. In contrast to discriminant analysis, backpropagation and Kohonen networks, the newly developed neural network architecture model of self-editing nearest neighbor nets (SEN3) provide the utility of incremental learning, i.e. the training phase must not be restarted each time when there is further information to learn. Trained SEN3 networks can be considered as ready-to-use knowledge bases and are appropriate to receive further morphometric data in a dynamic process that enhances the diagnostic power of such a network. For automated tumour grading all approaches yield similar grading results, however backpropagation networks only provide reliable results following an extensive training phase which requires the use of a supercomputer. All other neurocomputing models can be run on simple unix workstations. Based on the analysis of the morphometric features of minimum spanning trees, relative nuclear areas and relative volume weighted mean nuclear volumes of the proliferating nuclei the multivariately generated HOM grading system provide the highest correct grading rates, which were better than 90%, while the two widespreadly employed qualitative histological grading systems for astrocytoma yield correct grading rates of about 60%.2. IntroductionData-driven approaches play an important role in automated decision making, in contrast to knowledge-based methods. Data-driven methods are necessary when there is no precise knowledge about a phenomenon that allows its description in form of rules, Bayes networks or other form of explicite modelling. The main representatives of data-driven methods are the statistically based discriminant analysis, and from the field of artificial intelligence the neural network technology. For automated tumour grading purposes based on morphometric data these tools are extremely appropriate and valuable, since the boundaries of morphometric features for a given grading level are generally not well known. In the following publication we present several neural network models: Backpropagation, Kohonen, and SEN3, and compare the results of automated tumour grading with the classical statistical data driven approach of discriminant analysis. The following astrocytoma grading systems were analysed: The WHO grading scheme (Zülch, 1979), St. Anne-Mayo-system (Daumas-Duport et al., 1988) and a morphometricly based grading system (Kolles et al., 1994), that was denominated the HOM-system.3. Material and methodsThe numeric basis of this study are CT-guided, stereotactically gained astrocytoma biopsies of 86 patients. Hereby numerous biopsy specimens are taken along a stereotactical trajectory through the tumour. Most of the specimens were taken with Sedan's needle, in cases of highly vascularized tumours, stereotactic forceps were employed. Despite the minute size of these biopsies (Sedan's needle: 7-10 x 1-1,5 mm; forceps: 1 mm3) it is generally possible to evaluate the cell nuclei in 4 consecutive fields of vision (objective 40x). The cell nuclei are coloured with a combination of Feulgen and immunhistochemical Ki-67 (MIB1) staining of paraffin sections of 3 thickness after pretreatment in a microwave oven. By this staining method non-proliferating nuclei are coloured pale red, proliferating nuclei appear dark blue and the cytoplasm remains colourless.
The morphometric data of a total amount of 679 measured fields are feed to neural networks and to discriminant analysis whereby the following morphometric features were measured and described in detail in another paper [ ]:
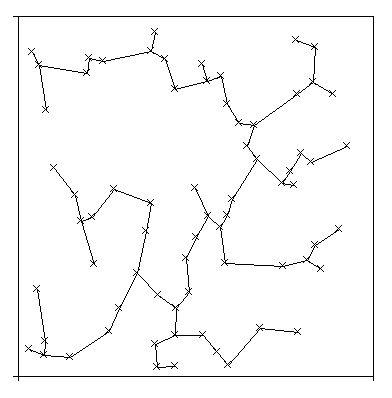
(ii) The mean value and (iii) the variation coefficient of the secant lengths of the minimal spanning trees: A parameter enabling the quantification of the growth pattern. (iv) Relative volume weighted mean nuclear volumes of the proliferating nuclei: A combined indicator of both proliferation tendency and nucleus pleomorphism.
 The WHO graduation system distinguishes astrocytoma (WHO grade II), anaplastic or malignant astrocytoma (WHO grade III) and glioblastoma (WHO grade IV). The binary St. Anne-Mayo-system (SAMS) is based on four morphologic criteria -nuclear atypia, mitosis, endothelial proliferation, and necrosis - which are determined by histological examination and summarized in a score:
3.1. Neural NetworksThe normed morphometric data were used to train and test three different neural network models: standard feedforward-backpropagation networks [Rummelhart86], specially adapted Kohonen feature maps [Kohonen88] [Rahmel&Wangenheim93] and a new model, capable of incremental learning, the SEN3-network. For each of the models networks were generated and trained independently for each of the grading scales: WHO, SAMS and HOM. A detailed description of the structure of input data can be found in [Kolles,v.Wangenheim..blabla]. The training set used for all network models was the same and consisted of a random-chosen subset of about 25% of the total amount of data.´3.1.1. BackpropagationThe backpropagation (BP) networks were chosen for this study because of their standard use and as a base of comparison of their results with those of the other models. Although BP-networks are shown to be theoretically able to represent any mapping between input and output data, given that at least one mapping exists [Hertz91], they have the disadvantages of all of the gradient descent procedures as being very computation intensive and being capable of falling into local minima. We used a parallel implementation of BP on a nCUBE2 supercomputer that was specially designed for the purpose of this study. The usual procedure we used was to train several networks with identical topologies and different random weight initializations and to compare the results. This is also cost intensive an drepresents another disadvantage of the BP procedure. Here the topologies were chosen with 1, 2 and 3 hidden layers and, at least, 3 network instances for each topology were trained. All networks were trained until the global output error remained nearly constant.3.1.2. KohonenThe Kohonen feature maps were implemented on Sun SPARC stations accordingly to suggestions made in [Ritter&Kohonen89] for the neighborhood function enhanced through a discretization of the input space [Rahmel&Wangenheim93] into value categories. Networks were trained with and without the inclusion of an output layer for the grading, which is trained on the grading output with the BP algorithm after complete training of the feature map. The main idea here is to map the input data (morphometric data) onto the Kohonen map an then to train the output layer with the desired grading output. When the output layer is not used, the complete training pattern with the 3 or 4 dimensions of grading classification is fed to the network during training, with the morphometric parameter part weighted 1.0 and the classification part weighted 0.2, as originally suggested in [Ritter&Kohonen89]. For the purpose of test and classification, only the morphometric data is presented to the network and the activation patterns are propagated back to the neurons of the input layer corresponding to the classification part of the input vector as suggested in [Rahmel&Wangenheim93]. When the training is done with the BP output layer, only the morphometric data are presented to the network.Kohonen's learning algorithm for topological feature maps can be interpreted as an approximation of a generalization of factor analysis [Ritter91]. In figure 2 a two dimensional example in a), b) and c) is shown. A two dimensional data distribution can be approximated through a main axis w1 that passes through the center of gravity w0 of this distribution and is defined by the eigenvectors of the correlation matrix of the largest eigenvalues of this distribution. Since this is a linear description, applying this procedure to "nonlinear" data distributions like in b) will result in a poor description. A Kohonen net is a discrete approximation of a "main curve" [Ritter91] (figure 2.c) where neurons map to areas defined by points on this curve. In the higher-dimensional case (figure 2.d), the Kohonen lattice spans a discrete "main surface" which approximates the data distribution and is represented through the weight vectors wr of each neuron. Each vector wr is associated to a volume Fr in the data space, representing a set of the input parameter values associated with the neuron with this weight vector. 3.1.3. SEN3 NetworksThe SEN3(Self-Editing Nearest Neighbor Net) combines the incremental construction of a network structure, as it occurs in ART [Grossberg87], with the intention of the Editing-Concept, as it was already used in early nearest-neighbor classification procedures. The linking element between those two approaches is the use of a neighborhood relationship between neurons as it appears in the Kohonen network and in the GCS (Growing Cell Structures) [Fritzke93]. After the nearest neighbor classification [Cover67] showed that it could be applied successfully in many areas, there were increasig efforts made in reducing the set of classificators for the test phase, in order to reduce the computational costs of the practical application of this classification method.These optimization procedures were brought together under the idea of the editing of the training set. One example of such a procedure is the in [Ritter75] proposed algorithm for the construction of a selective set of prototypes, which is a minimal subset of the training set. The beasic idea of the "editing" of the training set was adopted for the procedure of the construction of a SEN3-network. The optimality of the generated results, as in [Ritter75],is replaced here by the simplicity of training and the possibility of incremental extension of the coded information. Despite the loss of representation optimality, SEN3can reach suboptimal results that are very promising, mainly under the point of view of real applications with a huge ammount of data. Artificial neural networks, like the Kohonen network or the GCS, approximate the distribuition of the training data in the input space during the training process. An agglomeration of input vectors, e.g. often repeated or very similar data in the training set, leads to a stronger representation of these data in the net structure. One heuristic used in SEN3, when only classification is necessary, is the editing. If one wants to reduce the total number of prototypes in the mapping, it is better to reduce the density of prototypes in the center of some cluster and to keep the edges of the classes represented so sharp and with so much prototypes as possible, in the aime to describe the class borders as well as possible. 3.1.4. Construction of the SEN3 -Network:Figure 3 shows the construction process through a simple example. Suppose the set of training examples is divided into a start set (points inside the ellipse) and a set of incrementally added data points. The points in the example belong to two different classes, indicated by the color of the dots.The first step of the algorithm works on the elements of the start set. It creates a neuron for each data point, initializes the weight vector with the data vector and calculates the neighborhood relations among those neurons. In the example in figure 3.b each neuron is connected with its two best neighbors, but other connection schemes can be considered. The second step of the construction creates a neuron for each remaining data point (outside the ellipse in figure 3), again initializing the weight vector with the data values and connecting the new neuron with its two best neighbors. Figure 3.c) shows the resulting network, when the points are added in the sequence indicated by the numbers. The last step is the editing, which removes those neurons from the network, that are only connected with neurons in the same class. Figure 3.d shows, how the number of neurons is reduced, while an imagined class border remains well defined by the neurons near that line. Thus, there is both a considerable reduction of calculation time in the classification phase and also when new data is added to the edited network, while the classification power of the network is nearly preserved. The SEN3 networks were implemented as an extension of NeuralTalk, an at the University of Kaiserslautern in Smalltalk written simulator for neural networks. All simulations were done on a Sun SPARC workstation. 3.1.5. Representation capabilities of SEN3One of the most difficult tasks for classificator systems like neural networks is to find an adequate representation for data that show an intrincate non-linear distribution pattern. One well-known test for connectionist systems is the task to learn the Problem of the 2 Spirals. A bidimensional data distribution of 192 data vectors results in two classes that are distributed as two concentric spirals. This task is almost impossible to solve with standardgradient descent methods. Tests made with the SEN3-network results shown in figure 4. The data distribution is shown in 4.a). Figure 4.b) shows the decision areas of the data. Figure 4.c) shows the same areas as represented by the network after editing.4. ResultsAn overview of the results of the automated astrocytoma grading approach is shown in Fig. 5. The overall graduation results are about 60 % for the WHO and the SAMS graduation systems, while the HOM system has correct rates of about 100%. Within the grading systems there are no important differences concerning the quality of classification between the analysed data-driven approaches.The backpropagation networks presented the learning performance shown in figure 6 and within all tested methods, also presented the best generalization capabilities. The best results were obtained with networks with two hidden layers and a topology of 4:30:10:3 for the HOM-Scale, 4:50:20:3 for WHO and 4:30:10:4 for SAMS. The fastest learning behavior for the training set was shown for the HOM scale (fig. 6.a) which was learned up tp 99% after 100,000 epochs. The poorest results were presented by the SAMS scale, whose training set was learned just up to about 81% after exhaustive training of more than 800,000 epochs. For the WHO scale, more 96% of the training set was learned. All simulations were performed on a hypercube of dimension 4 and took up to 10 consecutive processing days with the 4:50:20:3 topology for the WHO scale. The generalization capabilities of the trained networks (fig. 6.b) were very poor for the WHO and SAMS scales and and near the training set performance for the HOM scale. The very good training set results together with the poor generalization for the WHO scale could turn out the question of "overtraining" of the in fact relative huge topology used for this scale (two hidden layers with respectively 50 and 20 neurons). This hypothesis was shown to be false with smaller networks, wich theoretically should present better "generalization" capabilities due to a better data compression through less neurons. Those networks presented poorer results with the training set and near the same generalization capabilities, which were up to 10% inferior when compared to the 4:50:20:3 topology. For further discussion of the BP results see [Kolles&Wangenheim]. In our study, we used Kohonen`s algorithm to map the morphometric input data onto a two dimensional feature map in two ways. First we used the Kohonen model alone and presented the complete morphometric and grading data during training. In the second, just morphometric data were trained with the Kohonen model with the aime to reduce complexity of data. The obtained Kohonen map was further mapped to the desired grading output with an one-layer BP-network. This combination turned out to be much faster than the use of pure BP since the Kohonen algorithm is much faster than BP and the "prepared" data from the Kohonen map are easier for the simple one-layered BP-net to learn and show a relative fast convergence, when compared to BP alone. The results of this approach were in the order of 1% better than the use of the Kohonen model alone, as is shown in table 1) below. The best results for the Kohonen maps were obtained for a 10x10 bidimensional map after 10,000epochs training for all scales and for both with and without output BP-layer. Training of the output layer (topology 100:3) took up to 40,000 epochs. These results were unexpected, since there should be a better performance for this model, due to the good representation powers of the Kohonen model (see above). The total processing time took about 12 hours for the Kohonen maps and about 12 hours for the training of the BP output layer, both on a SPARC2 station. The results for the SEN3-networks are shown in table 2) below. For the SAMS and HOM scales, they were just slightly inferior to the results shown by the BP-networks. The results for the WHO scale are even poorer as the results presented by discriminant analysis. Here one has to observe, however, that discriminant analysis was carried out with the whole data set, and not only with a "training" subset of the data, in such a way that it is not possible to speak of as "generalization" in the case of discriminant analysis. The generation and test of all SEN3-networks took less than 1 hour an a SPARC2 station with the Objectworks/Smalltalk80 4.1 interpreter. 5. DiscussionAll employed neural network topologies show similar results in automated glioma grading. There is no evidence that the mediocre results in automated glioma grading using the WHO or SAMS graduation are caused by a lack of expressiveness of the different neural network architectures. The morphometricly based HOM grading system for astrocytomas reaches the best results in automated grading. The quality criteria of the used approaches are listed in tab. 3.The standard statistical procedure of discriminant analysis can be considered as golden standard for the other presented approaches. Backpropagation networks only yield acceptable grading results following an extensive training phase of several days, which were demonstrated in an earlier investigation []. This is the reason why other types of neural networks were developped. Kohonen networks already provide reliable grading results after a clearly reduced training phase. Their main disadvantage, also shared by backpropagation and discriminant analysis, is the lack of incremental learning, i.e. the training phase must be restarted if there is further information to learn. Here the self-editing nearest neighboor neural networks (SEN3) provide a valuable tool combining both the feature of incremental learning and a very shortened training phase. Trained SEN3 networks can be considered as ready-to-use knowledge bases and are appropriate to receive further morphometric data in a dynamic process. All SEN3 networks are fully open to extension with new data, allowing the representation of huge training sets of 2000 or more cases with the possibility of a successive dynamic refinement of the knowledge base represented by a network. Even the training of BP networks with such a huge training set is unthinkable due to the very slow learning performance that the morphometric data showed. With SEN3 networks it is possible to construct an "automated graduator" (AG) consisting of a morphometric software supplying direct the necessary measured features to the neural network which in the first step updates its internal weight factors and then makes an automated grading proposition. The concept of an AG is only meaningful if there is a high degree of conformity between automated and non-automated tumour grading, which is only to observe in the multivariately generated HOM grading system. In a previous study [ ] we have investigated a vaste number of putative expressive morphometric featues. Based on the four presented morphometric parameters it was possible to define three distinct clusters corresponding to the grading levels of the HOM system. These HOM grading levels could be precisely reproduced in discriminant analysis while a similar parameter constellation could not be found reflecting the grading levels of the qualitative WHO and SAMS graduation systems. This is the reason why we consider these grading systems to be inappropriate for automated tumour grading. 6. References[Cover67] Cover, T.M., Hart, P.E.: Nearest Neighbor Pattern Classification, IEEE Transactions on Information Theory, Vol. IT-13, No. 1, 1967.[Fritzke93] Fritzke, B.: Growing Cell Structures - A Self-Organizing Network for Unsupervised and Supervised Learning, TR-93-026, ICSI, Berkeley, CA, 1993. [Grossberg87] Grossberg, S., Carpenter, G.: A Massively Parallel Architecture for a Self-Organizing Neural Pattern Recognition Machine, Computer Vision, Graphics and Image Processing, 1987. [Hertz91] Hertz,J., Krogh, A., Palmer, R.G.; Introduction to theory of neural computation, Santa Fé Institute, Studies in the Sciences of Complexity Series, Addison-Wesley, Redwood City, CA, USA, 1991. [Kohonen88] Kohonen, T.: Self-Organization and Associative Memory, 2nd. Ed., Springer Verlag, Munich, 1988. [Rahmel&Wangenheim93] Rahmel, J., v.Wangenheim, A.: The KoDiag System: Case-Based Diagnosis with Kohonen Networks, in: Lisboa, P.J.G., Taylor, M.J.: Proceedings of the Workshop on Neural Network Applications and Tools, Liverpool, IEEE Computer Society Press, 1993. [Ritter75] Ritter, G.L., Woodruff, H.B., Lowry, S.R., Isenhour, T.L.: An Algorithm for a Selective Nearest Neighbor Decision Rule, IEEE Transactions on Information Theory, Vol. IT-21, No. 6, 1975. [Ritter91] Ritter, H., Martinetz, Th., Schulten, K.: Neuronale Netze, 2. Ed., Addison Wesley, Bonn, 1991. [Ritter&Kohonen89] Ritter, H., Kohonen, T.: Self-Organizing Semantic Maps, Biological Cybernetics 61, pp 241-254, 1989. [Rummelhart86] Rummelhart,
D.E., McClelland, J.L. (eds.): Parallel Distributed Processing, Volume
1, MIT Press, 1986.
|
|
 |
 |